**深度优先搜索(DFS)**是一个重要的基础算法
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking ——wikipedia
维基的定义已经讲的很清楚了,深搜就是从一个点开始,走过的点标记,在周边找没走过的点,随意挑一个往下走,知道走不到了就回退到上一步,继续寻找没走过的点。这样的算法比起广搜(bfs)相对容易理解,也就是一步一步往前走,试图走得更远。
深搜的有两个用法
1、寻找路径
2、遍历每一个节点
接下来进行走法的举例

如果以1为起点,可以发现2、3都没被标记,于是任选一个
1 -> 2
同时标记1,走到2。2周边,只有4没被标记。于是
1 -> 2 -> 4
同时标记4,4周边,3、5、8都没被标记,任选一个
1 -> 2 -> 4 -> 3
标记3,3周边5、7未被标记,任选一个
1 -> 2 -> 4 -> 3 -> 5
标记5,5周边只有6没被标记
1 -> 2 -> 4 -> 3 -> 5 -> 6
标记6,只有8没被标记
1 -> 2 -> 4 -> 3 -> 5 -> 6 -> 8
标记8,这时我们就发现,8周围已经没有未被标记的数字了,那就沿着路经回退
8的上一个是6,6这时周围也已经没有数字,那就接着回退
6的上一个是5,5这时周围也已经没有数字,那就接着再回退
1 -> 2 -> 4 -> 3
5的上一个是3,3周围还有7未被标记,那就走7
1 -> 2 -> 4 -> 3 -> 7
接下来反复上面的规律
1 -> 2 -> 4 -> 3 -> 7 -> A (如果A是你想要寻找的到终点的路径,那么这是路径就已经形成,那这里我们目标是遍历所有节点,这就是我前面说到的深搜的两种用法)
继续模拟
1 -> 2 -> 4 -> 3 -> 7
1 -> 2 -> 4 -> 3 -> 7 -> 9
1 -> 2 -> 4 -> 3 -> 7
1 -> 2 -> 4 -> 3
1 -> 2 -> 4
1 -> 2
1
我相信深搜是如何运作的你已经非常明白了,那要如何实现呢
这就要用到pjwz最喜爱的递归了😀
下面直接放上伪代码
Node path[MAX_LEN]; //MAX_LEN取节点总数就好
int depth;
bool dfs(V){
if(V为终点){
path[depth] = V;
return true;
}
if(V被标记过)
return false;
将v标记;
path[depth] = V;
depth++;
再找与V相邻的每一个节点U{
if(dfs(u) == true)
return true;
}
depth--;
return false;
}
int main()
{
把所有点都标记成新点;
depth = 0;
if(dfs(起点)){
for(int i = 0; i <= depth; i++)
cout << path[i] << endl;
}
}
那么现在还要介绍一下两种图的表示方法
1、邻接矩阵
用二维数组G [i] [j] ,来存放图,G [i] [j] 表示节点i和节点j之间边的情况如(有无边,变方向,权值大小等)
遍历复杂的为O(n^2)
2、邻接表
每个节点V都对应一个一维数组,来存放与V连出去的边,边的信息包括另一节点等
拿图举例
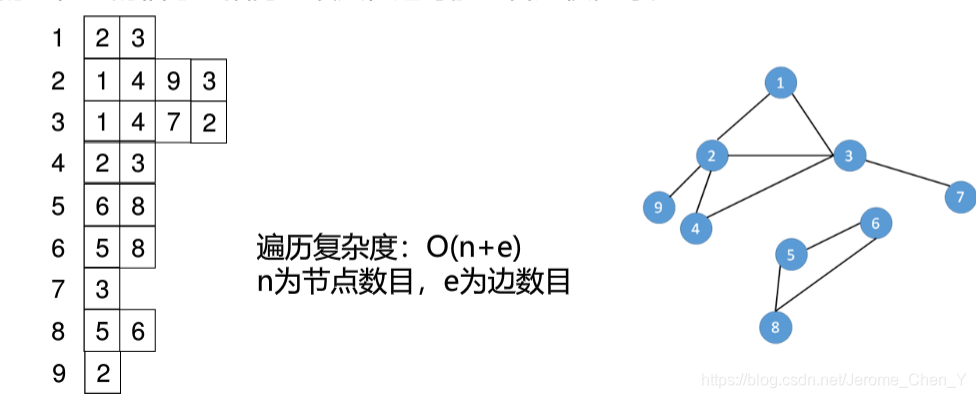
参考资料:北大算法课
310








 本文深入讲解深度优先搜索(DFS)算法,从定义出发,详细解释其工作原理与应用,包括路径寻找与节点遍历。通过实例展示DFS的具体操作流程,并提供伪代码帮助理解实现过程。此外,还介绍了邻接矩阵与邻接表两种图的表示方法。
本文深入讲解深度优先搜索(DFS)算法,从定义出发,详细解释其工作原理与应用,包括路径寻找与节点遍历。通过实例展示DFS的具体操作流程,并提供伪代码帮助理解实现过程。此外,还介绍了邻接矩阵与邻接表两种图的表示方法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








