数学漫游 ->奇异值分解SVD

奇异值分解(SVD)

前面提到对于方阵$A$, 大小为nxn, 在一定条件下, 可以进行特征值和特征向量分解. 但存在问题:

• 方阵$A$的特征向量并不正交(只有是对称矩阵的情况下才正交).
• 方阵$A$的特征向量数量不够(即不满足n个特征向量组是线性相关的).
• 并不是一个方阵(A可能并不是方阵).

这种情况下如何对大小为mxn的矩阵$A$ 进行分解呢? $A$的奇异向量能够完美地解决上述问题.

1. SVD的推导

目标: 寻找行空间的一组标准正交基, 作用$A$以后, 变换到列空间的一组正交基(倍数乘以标准正交基).
$$A{v}_1={\sigma }_1{u}_1,A{v}_2={\sigma }_2{u}_2,...,A{v}_r={\sigma }_r{u}_r$$
$v_i\in {\mathbb{R}}^n,u_i\in {\mathbb{R}}^m$
所以可以得到:
$$A\left[\begin{array}{ccc}{v}_1& ...& v_r\end{array}\right]=\left[\begin{array}{ccc}{u}_1& ...& u_r\end{array}\right]\left[\begin{array}{cccc}{\sigma }_1& & & \\ & .& & \\ & & .& \\ & & & {\sigma }_r\end{array}\right]\Rightarrow AV=U\Sigma$$
其中$V\in C(A^T)$, $A$的行空间, $U\in C(A)$, $A$的列空间. 如果矩阵 $A$ 的行列空间不满秩, 那么会对$U$和$V$补上相应数量的对应零空间中的单位正交向量成为方阵, 写成如下形式:
$$A\left[\begin{array}{ccccc}{v}_1& ...& v_r& ..& v_n\end{array}\right]=\left[\begin{array}{ccccc}{u}_1& ...& u_r& ..& u_m\end{array}\right]\left[\begin{array}{ccccc}{\sigma }_1& & & & \\ & .& & & \\ & & .& & \\ & & & {\sigma }_r& \\ & & & & \end{array}\right]\Rightarrow AV=U\Sigma$$
综上可以得到SVD的表达式:
$$A=U\Sigma V^{-1}=u_1{\sigma }_1{v}_1^T+...+u_r{\sigma }_r{v}_r^T$$
又因为, $V$是一个正交阵, 所以$V^T=V^{-1}$, 代入上式, 得:
$$A=U\Sigma V^{-1}=U\Sigma V^T$$

2. 如何求解 $U$ , $\Sigma$ 和 $V$

计算$A^{T}A$可以消去$U$:
$$A^{T}A=V{\Sigma }^T{U}^{T}U\Sigma V^T=V\left[\begin{array}{ccccc}{\sigma }_1^2& & & & \\ & .& & & \\ & & .& & \\ & & & {\sigma }_r^2& \\ & & & & \end{array}\right]V^T$$
可以发现, $A^{T}A$的结果恰好和$A^{T}A$的特征值分解的形式相同. 也就是说矩阵$V$由$A^{T}A$的特征向量组成, 特征值为${\sigma }_i^2$. 即我们求解特征方程 $A^{T}Av={\sigma }_i^{2}v$.

计算$A{A}^T$可以消去$V$
$$A{A}^T=U\Sigma V^{T}V{\Sigma }^T{U}^T=U\left[\begin{array}{ccccc}{\sigma }_1^2& & & & \\ & .& & & \\ & & .& & \\ & & & {\sigma }_r^2& \\ & & & & \end{array}\right]U^T$$
同理, $A{A}^T$的结果恰好和$A^{T}A$的特征值分解的形式相同. 也就是说矩阵$U$由$A{A}^T$的特征向量组成, 特征值为${\sigma }_i^2$. 即我们求解特征方程 $A{A}^{T}u={\sigma }_i^{2}u$.

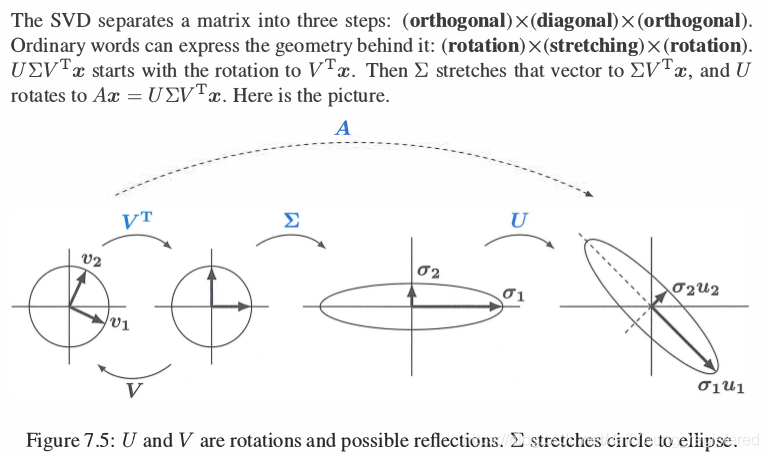
3. SVD的几何形式

从图中可以看出对矩阵A的SVD分解可以表示成一个圆到一个椭圆的变换过程.

4. 矩阵A的伪逆(Pseudoinverse)和SVD求解最小二乘

(1) 伪逆的定义
前面讲到任意大小的普通矩阵都可以奇异值分解. 从 $Av=\sigma u$ 出发进行推导. 如果$A$是一个可逆的方阵, 那么有 $A^{-1}u=\frac{1}{\sigma }v$. 那么相应的SVD分解形式也会变成:
$$A=U\Sigma V^T\Rightarrow A^{+}=V{\Sigma }^{+}{U}^T$$
其中的 $+$ 表示伪逆, 如果 $A$ 是方阵并且的确存在逆的话, 结果就是 $A$ 的逆. 但是如果矩阵 $A$ 的行空间不满秩或者列空间不满秩, 那么不管是不是方阵, 就会导致 $A$ 不存在逆. 这时候就定义矩阵 $A$ 的伪逆.

(2) SVD形式的伪逆应用求解最小二乘
在正交投影的章节中, 我们从几何的形式推导出, 求解最小二乘问题, 可以通过求解正规方程(normal equation).
$$A^{T}A\hat{x}=A^{T}b\Rightarrow \hat{x}=A(A^{T}A{)}^{-1}{A}^{T}b$$
这其中, 我们假设矩阵 $A$ 和 $A^{T}A$ 是可逆的. 现在如果 $A$ 不满秩, 那么就会导致正规方程存在多个解, 而不是唯一解. 原来 $Ax=b$ 中的A是满秩的, $b$ 不在 $A$ 的列空间中, 方程没有解, 因此需要求解最小二乘解. 如果 $A$ 不满秩, 则其中一个解为 $x^{+} = A^{+}b $ , 并且可以证明这个解 $x^{+}$ 是所有解最小的那个.
证明: TODO

总结

• 矩阵的特征值和特征向量分解适用于特定的矩阵, 对于任意大小的普通矩阵, 可以使用SVD分解.
• 矩阵 $A$ 将 $C(A^T)$ 中的一组标准正交基变换到 $C(A)$ 中的一组正交基. 由此可以推导出 $A=U\Sigma V^T$ 的分解形式.
• 通过 $A^{T}A$ 的对称矩阵形式可以消去 $U$ , 从而得到 $V$ 和 $\Sigma$ 的求解方式. 同理通过 $A{A}^T$ 的对称矩阵形式可以得到 $U$ 和 $\Sigma$ 的求解方式.

参考

[1] Strang G, Strang G, Strang G, et al. Introduction to linear algebra[M]. Wellesley, MA: Wellesley-Cambridge Press, 1993.