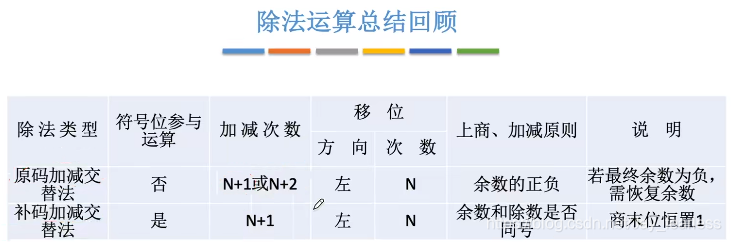
1.原码的除法运算(符号位单独计算)
恢复余数法
商0情况
先默认商1,如果不够减,就恢复余数商0.

商1情况

手动模拟
左移n次,上商次数为n+1n+1n+1次。

不恢复余数法(加减交替法)
当余数为正时,商1,余数左移一位,减去除数(+[−∣y∣]补[-|y|]_{补}[−∣y∣]补)。
当余数为负时,商0,余数左移一位,加上除数(+[∣y∣]补[|y|]_{补}[∣y∣]补)。

左移n次,上商次数为n+1n+1n+1次,所以加减要n+1n+1n+1次。
若最后一次的余数为负数,则要商0,并+[∣y∣]补[|y|]_{补}[∣y∣]补得到正确余数,故加减次数可能为n+2n+2n+2次。(不恢复余数法的最后一步可能要恢复余数。)
2.补码的除法运算(符号位参与运算双符号位)
刚开始被除数和除数同号,则被除数要减去除数(+[−y]补[-y]_{补}[−y]补);被除数和除数异号,则被除数要加上除数(+[y]补[y]_{补}[y]补)。
之后如果余数和除数同号,商1,余数左移,减去除数(+[−y]补[-y]_{补}[−y]补);
如果余数和除数异号,商0,余数左移,加上除数(+[y]补[y]_{补}[y]补)。
最后末位商恒置为1,不用看余数和除数的关系,一共进行n+1n+1n+1次加减。

原码不恢复余数与补码不恢复余数比较
3.数据类型强制转换
short 16bit,2字节
int、float 32bit,4字节
long、double 64bit,8字节

一般转换规律:char→int→unsigned→long->float->double
4.浮点数的表示和运算

浮点数尾数的规格化

规格化浮点数的特点

IEEE 754
阶码在IEEE 754标准中用移码表示。(移码只能表示整数)。
阶码真值=移码-偏移量
移码=阶码真值+偏移量
float有8位阶码:偏置值=28−1−1=1272^{8-1}-1=12728−1−1=127(移码:01111111B)
double有11位阶码:偏置值=211−1−1=10232^{11-1}-1=1023211−1−1=1023(移码:01111111111B)
尾数为原码表示,要通过移位让最高位为1,隐藏最高位,只写后面的M。

十进制数与单精度浮点数之间的转换

单精度、双精度所能表示的数据范围:
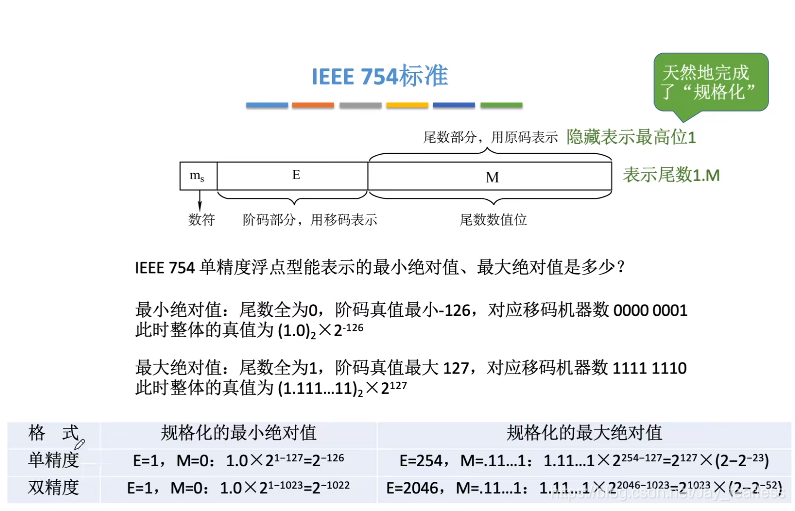
阶码全0,全1有特殊的用途
阶码全0,尾数M不全0,表示非规格小数,最高位隐含为0,阶码真值固定为-126。

浮点数的加减运算
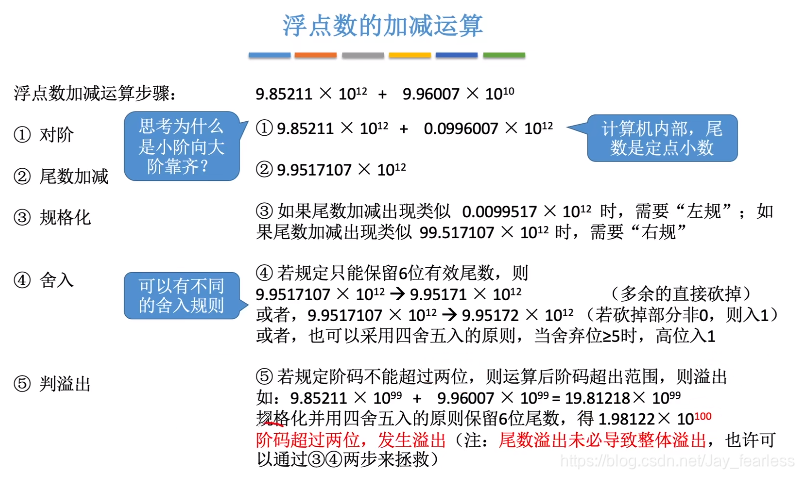
只有阶码溢出时会发生溢出,尾数溢出时未必导致整体溢出,可以通过规格化和舍入来拯救。
规格化具体操作

无舍入情况下的浮点数加减法

有舍入情况下的浮点数加减法
两种常用方法:'0’舍’1’入法,恒置’1’法

int->float 可能会损失精度
float->int 可能会损失精度,也可能会溢出

小结

5.ALU算术逻辑单元
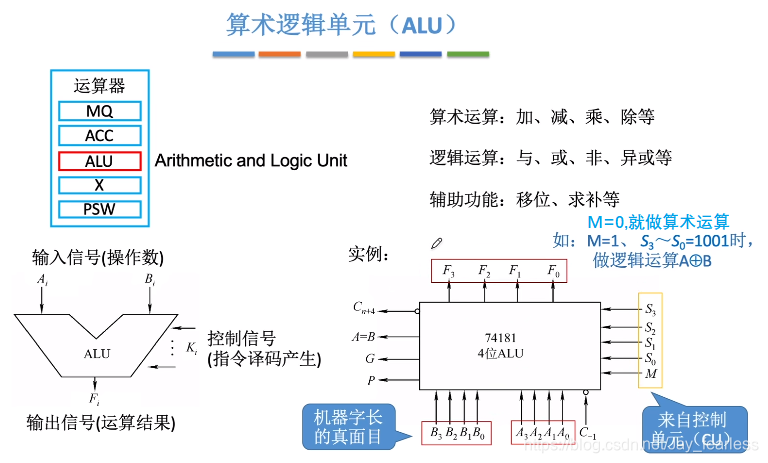
最基本的逻辑运算:与或非

复合逻辑:与非、或非、异或、同或

一位全加器


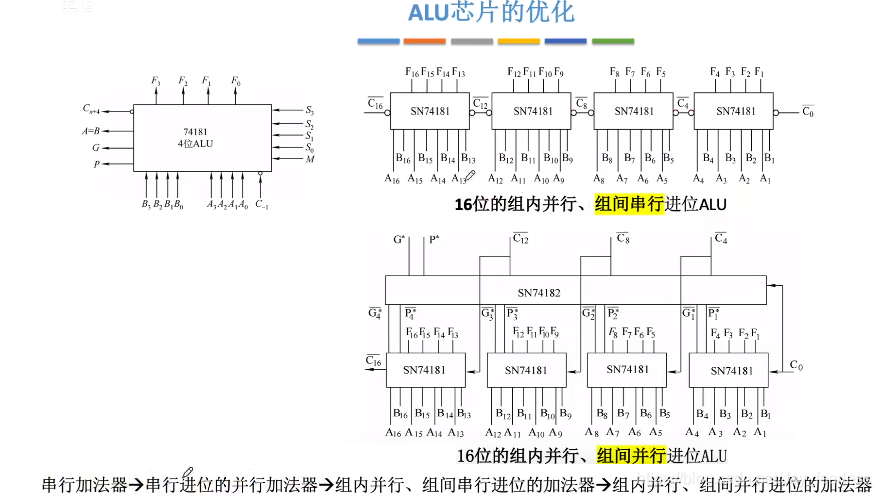
ALU芯片优化





 本文详细介绍了原码和补码除法运算的原理与步骤,包括恢复余数法和不恢复余数法,并对比了两者差异。同时,讨论了数据类型的强制转换,特别是从短整型到浮点型的转换可能带来的精度损失。此外,深入探讨了浮点数的表示、规格化和运算,以及IEEE754标准在浮点数运算中的应用。最后,简要概述了ALU算术逻辑单元的基本逻辑运算和优化策略。
本文详细介绍了原码和补码除法运算的原理与步骤,包括恢复余数法和不恢复余数法,并对比了两者差异。同时,讨论了数据类型的强制转换,特别是从短整型到浮点型的转换可能带来的精度损失。此外,深入探讨了浮点数的表示、规格化和运算,以及IEEE754标准在浮点数运算中的应用。最后,简要概述了ALU算术逻辑单元的基本逻辑运算和优化策略。

















 8341
8341

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










