CF855C Helga Hufflepuff‘s Cup(树形dp：用辅助数组来完成状态转移方程)

原创于 2022-04-25 12:01:40 发布 · 302 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划

CF 同时被 2 个专栏收录

17 篇文章

订阅专栏

动态规划

14 篇文章

订阅专栏

本文讨论了一个涉及树结构的问题，如何用状态转移方程准确计数以每个节点为根的子树中最高值节点的数量。通过引入辅助数组避免重复计算，解决了初始化值的乘法与加法的矛盾，展示了在动态规划中的巧妙应用。

题目链接

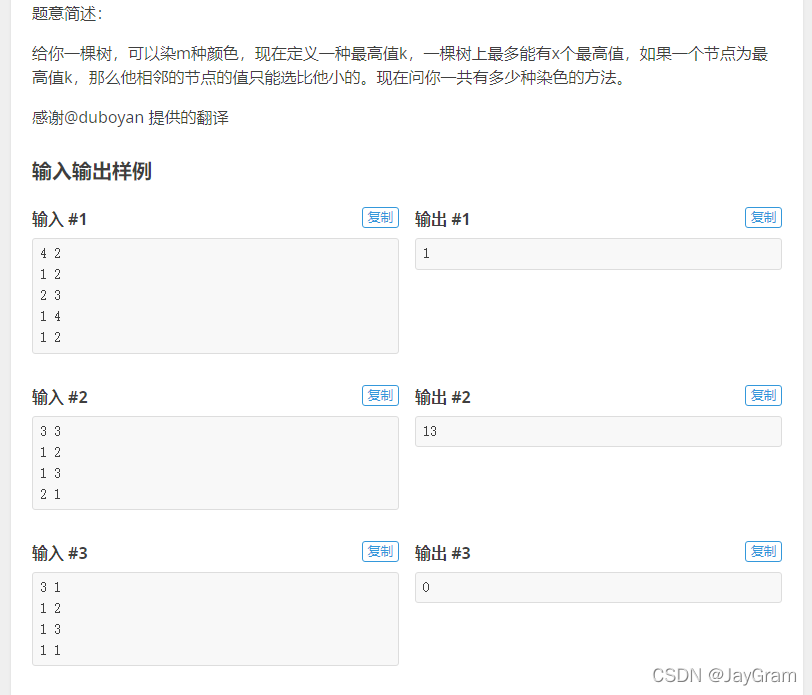
该题的状态表示挺好想的。

就是f[i][j[k]表示以i为根的子树有k个最高值。其中j有三个状态：

j=0时，表示i点的值为小于最高值

j=1时，表示i点的值为等于最高值

j=2时，表示i点的值为大于最高值

初始状态下f[i][0][0]=k-1;f[i][1][1]=1;f[i][2][0]=m-k;(m表示有多少种颜色)

但是在写状态转移的时候发现若正常的状态转移要有一些限制条件。

比如：在u从v中转移过来是f[u][0][j]+=f[u][0][j-k]*(f[u][0][k]+f[u][1][k]+f[u][2][k])%mod;

但是这样的话，会把初始化的值再加一遍。应该是把初始化的值乘上去。

但是若改为f[u][0][j]*=f[u][0][j-k]*(f[u][0][k]+f[u][1][k]+f[u][2][k])%mod;

那么不同的方案之间又变成相乘，又不行。

所以加个辅助数组g，先把值存在g当中，之后再转移到f数组即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
const int maxn=1e5+50;
LL n,m,idx,K,x;
int h[maxn];
int cnt[maxn];
LL f[maxn][3][15],g[3][15];
struct Edge{
    int v,nxt;
}edge[maxn<<1];
void add(int u,int v){
    edge[idx].v=v;
    edge[idx].nxt=h[u];
    h[u]=idx++;
}
int dfs(int u,int root){
    f[u][0][0]=(K-1)%mod;f[u][1][1]=1;f[u][2][0]=(m-K)%mod;
    cnt[u]=1;
    for(int i=h[u];~i;i=edge[i].nxt){
        int v=edge[i].v;
        if(v==root) continue;
        cnt[u]+=dfs(v,u);
        memset(g,0,sizeof(g));
        for(int j=0;j<=cnt[u]&&j<=x;j++){
            for(int k=0;k<=cnt[v]&&k<=j;k++){
                g[0][j]=(g[0][j]+f[u][0][j-k]*(f[v][0][k]+f[v][1][k]+f[v][2][k])%mod)%mod;
                g[1][j]=(g[1][j]+f[u][1][j-k]*f[v][0][k]%mod)%mod;
                g[2][j]=(g[2][j]+f[u][2][j-k]*(f[v][0][k]+f[v][2][k])%mod)%mod;
            }
        }
        for(int j=0;j<=cnt[u]&&j<=x;j++){
            f[u][0][j]=g[0][j];
            f[u][1][j]=g[1][j];
            f[u][2][j]=g[2][j];
        }
    }
    return cnt[u];
}
void solve(){
    memset(h,-1,sizeof(h));
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<n;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v);add(v,u);
    }
    scanf("%lld%lld",&K,&x);
    dfs(1,1);
    LL ans=0;
    for(int i=0;i<=x;i++){
        ans=(ans+f[1][0][i]+f[1][1][i]+f[1][2][i])%mod;
    }
    cout<<ans<<endl;
}
int main(){
    int t;t=1;
    while(t--) solve();
    return 0;
}