【B+树操作实例】实例讲解插入、删除元素的过程

基本概念

B+树是B树的变种，常用于数据库和操作系统的文件系统中。由于B+树的非叶节点只存有其子树的的索引，而真正的数据元素都在同一层，即都在叶节点上，所以其插入与删除元素具有稳定的对数时间复杂度。对于一棵m阶的B+树（m代表子树的最大数量），有如下特性：

1. 每个节点至多有m个子树
2. 除根结点外，每个结点至少有[m/2]个子女，根结点至少有两个子女
3. 有k个子女的结点必有k个关键字

实例讲解

对B+树的插入和删除操作可以遵循以下口诀：

以4阶B+树为例，假设非叶节点保存的关键字是子节点的最大值。

在插入新元素的过程中，如果插入的元素小于该节点的最大值且未过饱和，插入结束（实例1）；若插入的元素为该节点的最大值，这种情况只会发生在处于兄弟子树最右侧的节点，需要替换父类中相应的关键字（实例2）；如插入元素后该节点过饱和，则该节点分裂成两个，并更新父节点的关键字（实例3）。

删除元素可以分成3种情况：如果删除的元素小于所处节点的最大值，删除操作结束（实例4）；如果删除的元素时所处节点的最大值，则需要更新父节点的关键字（实例5）；如果所处节点删除该元素后元素数量小于2，则需要与兄弟节点合并，并更新父节点的关键字（实例6）。

如果看过我的【B树操作】实例讲解插入、删除元素 作可以遵循以下口诀，可以发现与之相比，B+树的口诀少了“上溢”和“下移”两个概念，因为在B+树中全部元素都是保存在同一层（叶节点）的，如果过饱和或元素数量不足都是横向拓展或收缩，只有在非叶节点记录的关键字数量过饱和时才会向上溢出。

实例1

 在插入7的过程中，7小于8，进入（3，6，8）得到（3，6，7，8），不需要更新父节点的关键字，插入操作结束。

实例2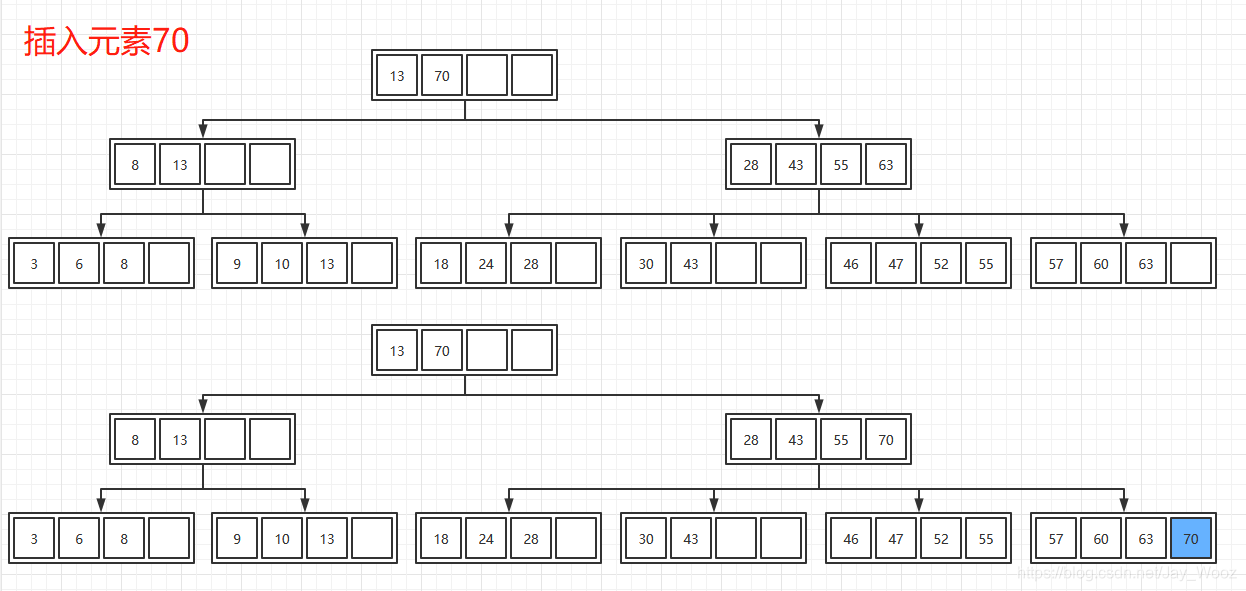

在插入70到（57，60，63）的过程中，因为70 比63大，所以插入70后节点变成（57，60，63，70），且更新父节点相对应的关键字63为70。

实例3

向节点（46，47，52，55）插入元素54后得到过饱和的（46，47，52，54，55），需要分裂成（46，47，52）和（54，55）两个节点，并将两个新节点的关键字替换掉父节点原本的55，使父节变成（28，43，52，55，70），此时父节点又达到过饱和，所以继续相似的操作，父节点也分裂得到（28，43，52）和（55，70），并更新根节点为（13，52，70）。

实例4

6不是所处节点的最大值，删除后不需要更新父节点关键字，删除操作结束。

实例5

在删除元素8时，节点（3，6）的最大值换成6，需要更新父节点的关键字。思考一下：在B树的删除操作中，我们总想向上接元素，但是在B+树里，每个关键字对应一个子树，所以只要子树数量不变，对父节点的影响就只是更新关键字。

实例6

删除元素30后，节点（43） 元素数量少于2所以需要和左边的兄弟节点合并并更新父节点中的关键字。

总结

相较于B树而言，插入或删除元素的操作都更加简单和直观，归结起来的口诀：

如果你遇到的情况不在上面六种实例中，欢迎私信或留言让我补充~