HyperLogLog原理及Redis实现分析

在某次需求实现时，面临的业务场景是对千万级的用户id做去重。Set、HashMap等常用的数据结构都能处理这种情况，但是这些数据结构也面临这样的问题：随着数据量的增多，占用的内存空间会越来越大。

出于对人力成本和内存资源消耗的考虑，最终我们选用了HyperLogLog来完成这一任务。

什么是HyperLogLog？一个(有限)集合里不同的元素个数就称为该集合的基数(cardinality)，HyperLogLog是一种在大数据量下统计基数的算法，标准误差为0.81%。相较于其它算法，HyperLogLog的一个明显优势就是仅需要12KB内存，就可以对大数据量级的数据进行基数统计。

在确定了0.81%的误差可接受之后，我们用pfadd的结果来判断用户id是否为重复id进行去重，预期是将误差控制在官方所说的0.81%左右。但结果却与预期的大相径庭，千万的用户id集合经过这样的去重过程，其中90%以上的id都被误判为重复id。为什么会产生如此大的差异呢？本文将从基数统计算法演进的过程出发，带大家了解HyperLogLog的算法原理，并向大家介绍Redis中HyperLogLog的具体实现，最后将通过一系列的实验去探讨这一问题的成因。

1. 基数统计算法演进

1.1 线性计数算法(Linear Counting)

线性计数算法是由Whang等人在1990年提出的算法，它整体的算法流程是：

下图是原论文中的一个例子，可以看到，使用上述过程，预估到的集合基数为

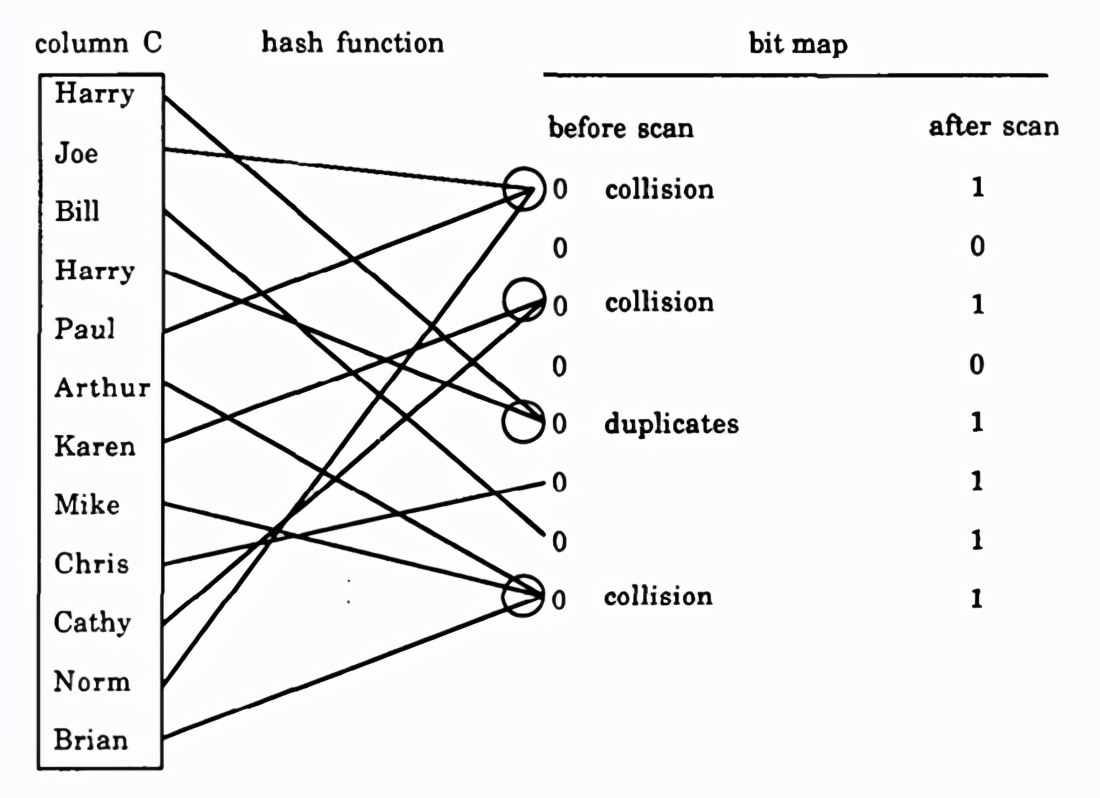
线性计数算法的流程比较简单，相较于bitmap，它的空间存储方面小有提升，但实际应用所需的空间复杂度仍为。

1.2 对数计数算法(LogLog Counting)

对数计数算法(简称LLC)基本思想是：将集合中所有元素做哈希，生成一个长度固定的比特串，令表示比特串中第一个“1”出现的位置，表示所有元素哈希得到的比特串中的最大值，那么集合总量可近似估计为：

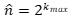
为什么可以采用这种方式估计呢？因为比特串的每个比特都独立且服从0-1分布，那么扫描比特串寻找第一个“1”的过程，从统计学角度就可以认为是一次伯努利过程。类比于抛硬币试验，就可以看作不断抛掷一枚硬币直到得到一个正面的过程。那么进行次伯努利过程，所有投掷次数都不大于的概率为：

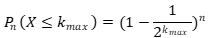
至少有一次不小于的概率为：

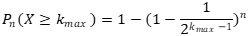
因此，

所以一旦集合中出现，那么从概率上讲的值即不可能远大于，也不会远小于，因此可作为基数的一个粗略估计。

不过如果直接使用单一的估计量进行基数估计，可能会因偶然性存在较大误差。所以LLC采用了均值法来尽可能地消减误差。基于上述思想，对数计数算法的整体流程如下：

假设hash结果定长 L 为32位。前10位用于桶编号，因此记录每个桶的，仅需要5bit()。能统计到的最大基数个数为，实际占用的内存为。这也就是算法名称中LogLog的由来。

但因为LLC使用的是算术平均数，对于离群值