通过计算实例简单地理解PatchCore异常检测

通过计算实例简单地理解PatchCore异常检测

• 前言
• 相关介绍

• PatchCore的工作原理：
• 优点：
• 缺点：

• 通过计算实例简单地理解PatchCore异常检测

• 总体流程
• 训练阶段

• 训练数据(正常图像)
• 特征提取
• Coreset 采样(假设 coreset_ratio=0.5 → K=4)

• 预测阶段

• 测试数据
• 特征提取
• 计算最近邻距离(输出异常分数)
• 异常分数图生成

• 参考文献

前言

• 由于本人水平有限，难免出现错漏，敬请批评改正。

相关介绍

• [1]  PatchCore 源代码地址：https://github.com/amazon-science/patchcore-inspection.git
• [2]  PatchCore 论文地址：https://arxiv.org/abs/2106.08265

PatchCore是一种用于异常检测的方法，它特别适用于工业视觉检查和其他需要在未见过的正常样本上进行训练的应用场景。这种方法是一种无监督或半监督学习方法。

PatchCore的工作原理：

1. 数据预处理：将输入图像分割成多个局部区域(patch)。
2. 特征提取：使用预先训练好的卷积神经网络(CNN)提取每个patch的特征向量。
3. 背景建模：构建一个背景模型来估计正常patch的分布。这通常是通过计算各个层激活的相似性矩阵，并使用这些矩阵来构建近邻图。
4. 异常得分计算：对于一个新的输入图像，计算其patch与背景模型之间的距离，从而得到异常得分。如果得分高于某个阈值，则认为该图像存在异常。

优点：

• 简单快速：不需要对特定任务进行额外的训练，只需要预先训练好的模型。
• 适应性强：可以应用于多种类型的图像数据和不同领域的应用场景。
• 资源效率高：内存占用相对较小，因为只需要存储少量的参考样本。
• 可扩展性：能够随着新的正常样本的增加而更新背景模型。

缺点：

• 依赖于高质量的特征提取器：特征提取的质量直接影响到异常检测的效果。
• 阈值设定：需要人为设置阈值来区分正常和异常样本，这可能需要一定的专业知识和经验。
• 对背景模型的选择敏感：不同的背景建模技术可能会导致显著不同的结果。
• 可能忽略全局信息：由于是基于局部patch进行分析，因此可能会忽略图像中的全局结构信息。

总体来说，PatchCore提供了一种高效且易于实现的异常检测方法，尤其适合于那些难以获得大量标注异常样本的情况。然而，在应用时也需要根据具体问题的特点选择合适的参数和背景模型。

通过计算实例简单地理解PatchCore异常检测

总体流程

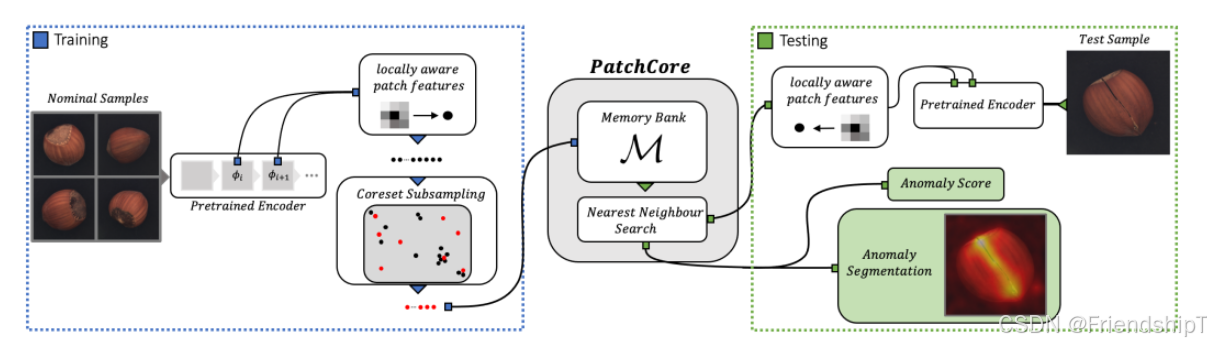
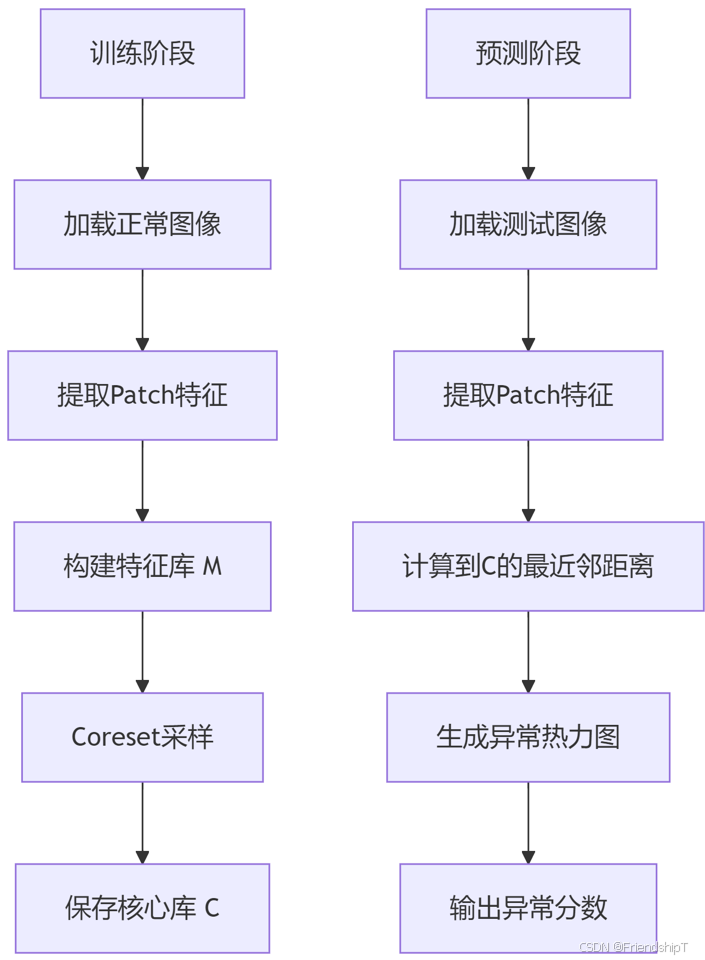
训练阶段

训练数据(正常图像)

登录后复制

# 图像1 (正常)
[ [1, 1, 1],
  [1, 1, 1],
  [1, 1, 1] ]

# 图像2 (正常)
[ [2, 2, 2],
  [2, 2, 2],
  [2, 2, 2] ]

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.

特征提取

登录后复制

# 图像1的特征提取
原始图像：
[[1,1,1],
 [1,1,1],
 [1,1,1]]

划分为4个Patch：
Patch1 (左上): [[1,1],[1,1]] → 特征 = [mean=1.0, max=1.0] → [1.0, 1.0]
Patch2 (右上): [[1,1],[1,1]] → [1.0, 1.0]
Patch3 (左下): [[1,1],[1,1]] → [1.0, 1.0]
Patch4 (右下): [[1,1],[1,1]] → [1.0, 1.0]

# 图像2的特征提取
原始图像：
[[2,2,2],
 [2,2,2],
 [2,2,2]]

Patch1: [2.0, 2.0]
Patch2: [2.0, 2.0]
Patch3: [2.0, 2.0]
Patch4: [2.0, 2.0]

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.

登录后复制

训练图像1 (3x3像素)     训练图像2 (3x3像素)
┌───────┐              ┌───────┐
│ 1 1 1 │              │ 2 2 2 │
│ 1 1 1 │  特征提取     │ 2 2 2 │  特征提取
│ 1 1 1 │  ========>   │ 2 2 2 │  ========> 
└───────┘              └───────┘

特征图 (2x2网格，每个单元代表一个Patch的特征向量):
┌───────────┬───────────┐
│ [1.0,1.0] │ [1.0,1.0] │   <- 图像1的四个Patch特征
├───────────┼───────────┤
│ [1.0,1.0] │ [1.0,1.0] │
└───────────┴───────────┘

┌───────────┬───────────┐
│ [2.0,2.0] │ [2.0,2.0] │   <- 图像2的四个Patch特征
├───────────┼───────────┤
│ [2.0,2.0] │ [2.0,2.0] │
└───────────┴───────────┘

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.

关键说明：

1. 每个3x3图像被划分为2x2=4个Patch
2. 每个Patch提取两个特征值：[平均值, 最大值]
3. 正常图像的所有Patch特征高度一致

Coreset 采样(假设 coreset_ratio=0.5 → K=4)

登录后复制

原始特征库 M = 8个点: 
    [1,1], [1,1], [1,1], [1,1], [2,2], [2,2], [2,2], [2,2]
步骤：
1. 随机选择初始点：比如 [1.0, 1.0]
2. 计算所有点到当前核心库的距离：
   - 到 [1.0,1.0] 的距离：
     [1.0,1.0]: 0
     [2.0,2.0]: √[(2-1)²+(2-1)²] = √2 ≈ 1.41
3. 选择最远点 [2.0,2.0] 加入核心库
   
4. 计算所有点到当前核心库的距离：
   - 到最近点的距离：
     [1.0,1.0]：min(到[1.0,1.0]=0, 到[2.0,2.0]=1.41) → 0
     [2.0,2.0]：min(0, 1.41) → 0
5. 所有点距离为0？随机选择下一个点 [1.0,1.0](但已存在)

最终核心库 C(K=4)：
C = [
  [1.0, 1.0],
  [2.0, 2.0],
  [1.0, 1.0],  # 重复点，实际会去重
  [2.0, 2.0]   # 重复点
]

去重后：
C = [
  [1.0, 1.0],
  [2.0, 2.0]
]

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.
• 28.
• 29.

Coreset作用：

• 原始8个点 → 压缩为2个代表点
• 保持原始分布特征(两个聚类中心)
• 计算效率提升4倍

登录后复制

原始特征库 M = 8个点: 
    [1,1], [1,1], [1,1], [1,1], [2,2], [2,2], [2,2], [2,2]

Coreset采样 (K=4):
1. 随机选起点: 选择 [1,1] -> C = [[1,1]]
2. 计算所有点到C的距离:
   - [1,1]: 0
   - [2,2]: √[(2-1)²+(2-1)²] = √2 ≈ 1.41
3. 选最远点 [2,2] 加入C -> C = [[1,1], [2,2]]
4. 重新计算距离:
   - 所有点距离为0 (因M中只有两种点)
5. 随机选两个点补充 (因K=4): 
   C = [[1,1], [2,2], [1,1], [2,2]]
6. 去重后核心库: C = [[1,1], [2,2]]

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.

预测阶段

测试数据

登录后复制

训练图像1 (正常)       训练图像2 (正常)       测试图像 (右下角异常)
┌───┬───┬───┐          ┌───┬───┬───┐          ┌───┬───┬───┐
│ 1 │ 1 │ 1 │          │ 2 │ 2 │ 2 │          │ 1 │ 1 │ 1 │
├───┼───┼───┤          ├───┼───┼───┤          ├───┼───┼───┤
│ 1 │ 1 │ 1 │          │ 2 │ 2 │ 2 │          │ 1 │ 1 │ 1 │
├───┼───┼───┤          ├───┼───┼───┤          ├───┼───┼───┤
│ 1 │ 1 │ 1 │          │ 2 │ 2 │ 2 │          │ 1 │ 1 │10 │
└───┴───┴───┘          └───┴───┴───┘          └───┴───┴───┘

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.

特征提取

登录后复制

测试图像：
[[1,1,1],
 [1,1,1],
 [1,1,10]]  # 右下角异常

Patch1 (左上): [[1,1],[1,1]] → [1.0, 1.0]
Patch2 (右上): [[1,1],[1,1]] → [1.0, 1.0]
Patch3 (左下): [[1,1],[1,1]] → [1.0, 1.0]
Patch4 (右下): [[1,1],[1,10]] → [mean=(1+1+1+10)/4=3.25, max=10] → [3.25, 10.0]

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.

计算最近邻距离(输出异常分数)

登录后复制

核心库 C = = [
  [1.0, 1.0],
  [2.0, 2.0]
]
测试特征 vs 核心库 C:
1. Patch1 [1.0, 1.0]:
   - 到 [1.0,1.0]距离 = 0
   - 到 [2.0,2.0]距离 = √[(1)²+(1)²] = √2 ≈ 1.41
   → 最近邻距离 = min(0, 1.41) = 0

2. Patch2 [1.0, 1.0]: 同上 → 0

3. Patch3 [1.0, 1.0]: 同上 → 0

4. Patch4 [3.25, 10.0]:
   - 到 [1.0,1.0]距离 = √[(3.25-1)² + (10-1)²] = √[5.0625 + 81] = √86.0625 ≈ 9.28
   - 到 [2.0,2.0]距离 = √[(3.25-2)² + (10-2)²] = √[1.5625 + 64] = √65.5625 ≈ 8.10
   → 最近邻距离 = min(9.28, 8.10) = 8.10

异常分数 = max([0.0, 0.0, 0.0, 8.10])=8.10

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.

异常分数图生成

登录后复制

块级异常分数：
[ [0.0, 0.0],   # 对应Patch1和Patch2
  [0.0, 8.10] ] # 对应Patch3和Patch4

上采样到像素级 (3×3):
每个像素值 = 覆盖该像素的所有块分数的平均值
最终热力图:
┌───────┬───────┬───────┐
│ 0.00  │ 0.00  │ 0.00  │
├───────┼───────┼───────┤
│ 0.00  │ 2.025 │ 4.05  │
├───────┼───────┼───────┤
│ 0.00  │ 4.05  │ 8.10  │
└───────┴───────┴───────┘

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.

参考文献

[1]  PatchCore 源代码地址：https://github.com/amazon-science/patchcore-inspection.git
[2]  PatchCore 论文地址：https://arxiv.org/abs/2106.08265
[3] https://link.springer.com/content/pdf/10.1007/s11263-020-01400-4.pdf
[4] https://www.mvtec.com/company/research/datasets/mvtec-ad/