连续邮资问题:
1.问题描述
假设国家发行了n种不同面值的邮票,并且规定每张信封上最多只允许贴m张邮票。连续邮资问题要求对于给定的n和m的值,给出邮票面值的最佳设计,在1张信封上可贴出从邮资1开始,增量为1的最大连续邮资区间。
例如,当n=2、m=3时,如果面值分别为1、4,则在l-6之间的每一个邮资值都能得到(当然还有8、9和12);如果面值分别为1、3,则在1-7之间的每一个邮资值都能得到。可以验证当n=2、m=3时,7就是可以得到连续的邮资最大值,面值为l、3。
当n=5和m=4时,面值为(1,3,11,15,32)的5种邮票可以贴出邮资的最大连续邮资区间是1到70。
2.问题分析
此问题为回溯和动态规划综合运用的问题:
基本思路:搜索所有可行解,找出最大连续邮资区间的方案
解向量:用n元组x[1:n]表示n种不同的邮票面值,并约定它们从小到大排列。x[1]=1是唯一的选择。
可行性约束函数:已选定x[1:i-1],最大连续邮资区间是1—r,接下来x[i]的可取值范围是x[i-1]+1—r+1。
如何确定r的值:计算X[1:i]的最大连续邮资区间在本算法中被频繁使用到,因此势必要找到一个高效的方法。考虑到直接递归的求解复杂度太高,
y[k]:不超过m张面值为x[1:i]的邮票贴出邮资k所需的最少邮票数。通过y[k]可以很快推出r的值。事实上,y[k]可以通过递推在O(n)时间内解决:
for (int j=0; j<= x[i-2]*(m-1);j++)
if (y[j]<m)
for (int k=1;k<=m-y[j];k++)
if (y[j]+k<y[j+x[i-1]*k]) y[j+x[i-1]*k]=y[j]+k;
while (y[r]<maxint) r++;
在函数Backtrack中,当i>n时,表示算法已搜索至一个叶结点,得到一个新的邮票面值设计方案x[1:n]。如果该方案能贴出的最大连续邮资区间大于当前已找到的最大连续邮资区间maxvalue,则更新当前最优值maxvalue和相应的最优解bestx。
当i<=n时,当前扩展结点Z是解空间中的一个内部结点。在该结点处x[1:i-1]能贴出的最大连续邮资区间为r-1。因此,在结点Z处,x[i]的可取值范围是[x[i-1]+1:r],从而,结点Z有r-x[i-1]个儿子结点。算法对当前扩展结点Z的每一个儿子结点,以深度优先的方式递归的对相应的子树进行搜索。
3.程序代码
#include <stdio.h> #include <string.h> int n, m;//n为邮票种类,m为一封信上最多贴的邮票个数 int Maxvalue;//最终最大邮资区间 int bestx[100];//最终最佳面值方案 //能否用t种邮票,面值在x数组中,最多贴m张,表示出sum(是个动态规划问题,方法是求出y[t][sum]看它是否小于m,状态转移方程y[i][j]=min(y[i-1][j-k*x[i]]+k) //其中y[i][j]表示用到第i种邮票,表示邮资为j的最少邮票数 int judge(int x[100], int t, int sum) { int i, j, k; int y[10][1000]; for (i = 0; i <= t; i++) y[i][0] = 0; for (i = 0; i <= sum; i++) y[1][i] = i; for (i = 2; i <= t; i++) for (j = 1; j <= sum; j++) { y[i][j] = 10000;//把k=0时的y值获取到 for (k = 0; k <= j / x[i]; k++)//要y取最小,所以应该尽可能的使用最大面值的x[i],最多能用j/x[i]张 if(y[i][j]>y[i - 1][j - x[i] * k] + k)//找最小的y y[i][j] = y[i - 1][j - x[i] * k] + k; } if (y[t][sum]>m) return 0; return 1; } void Backtrack(int x[100], int cur, int max) { int i, j, next; if (cur == n)//如果已经得出了n种邮票 { if (max>Maxvalue)//并且它的最大值已经大于当前最大邮资数 { Maxvalue = max; for (i = 1; i <= cur; i++) bestx[i] = x[i];//更新答案数组 } return; } for (next = x[cur] + 1; next <= max + 1; next++)//如果还没得到n种邮票,那么从x[cur]+1~max+1选一个作为下一个邮资,因为max+1没法表示,所以必定到max+1为止 { x[cur + 1] = next;//用种类为cur+1,数目分别为x[1..cur+1]的邮票,最多使用m张,能否表示出大于max的某个数 for (i = max + 1; i <= m * x[cur + 1]; i++)//i为加入新邮票之后能达到的最大值,这个数最少要为max+1,最多是x[cur+1]*m if (judge(x, cur + 1, i) == 0)//等于0说明超过了m,此时的i不成立,如果成立则返回1,i++ break; if (i>max + 1)//如果至少让最大值更新了一次(最大值有所更新,继续加入下一个邮票) Backtrack(x, cur + 1, i - 1);//上层for循环得到i之后又判断了i+1,所以i-1 } } int main() { int i, j, max, cur; int x[100];//中间传递的数组,存储当前的邮票值的解 printf("请输入发行邮票的种类:\n"); scanf("%d", &n); printf("请输入每张信封最多允许贴的邮票张数:\n"); scanf("%d", &m); Maxvalue = 0; max = m;//max表示到目前为止的最大可到达邮资 cur = 1; x[cur] = 1; Backtrack(x, cur, max);//x存储当前的解,cur表示当前传递到第几种邮票,max表示目前能表示到的最大值 printf("最佳设计方案:\n"); for (i = 1; i <= n; i++) printf("%d ", bestx[i]); printf("\n最大邮资区间为 %d\n", Maxvalue); system("pause"); return 0; }
4.输入输出示例
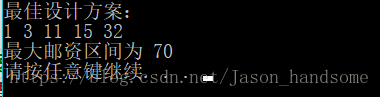





 本文介绍了连续邮资问题,探讨如何设计邮票面值以获得最大的连续邮资区间。通过回溯和动态规划的方法,分析问题并提供程序代码,展示如何在给定条件下找到最优解。
本文介绍了连续邮资问题,探讨如何设计邮票面值以获得最大的连续邮资区间。通过回溯和动态规划的方法,分析问题并提供程序代码,展示如何在给定条件下找到最优解。
















 2460
2460

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








