例题
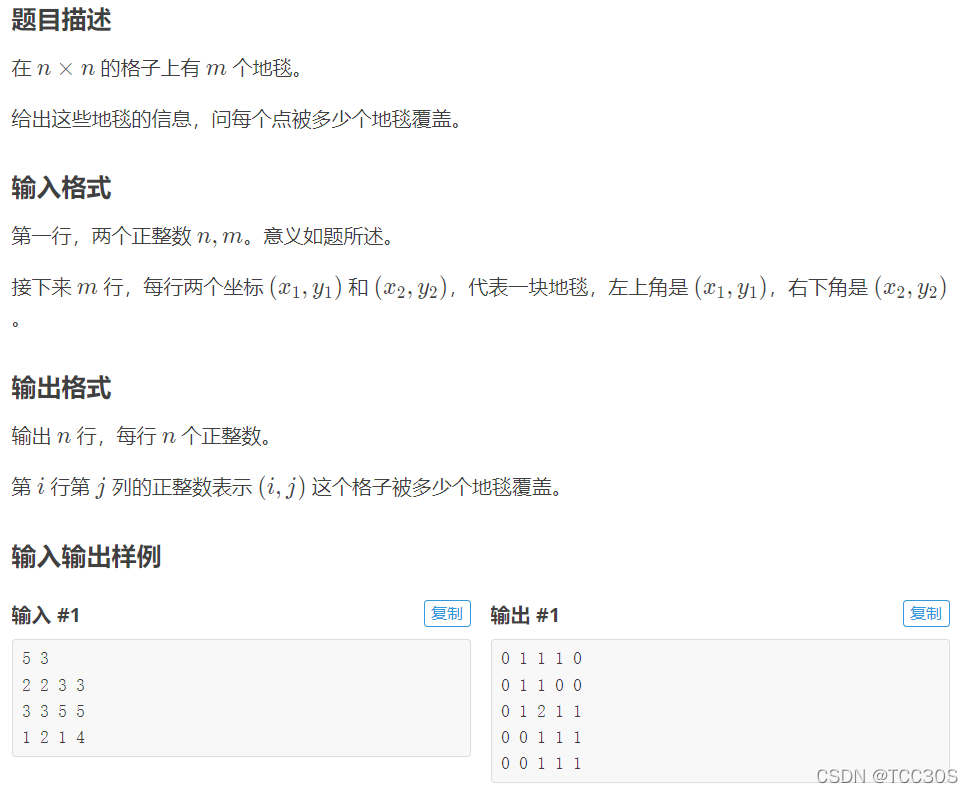
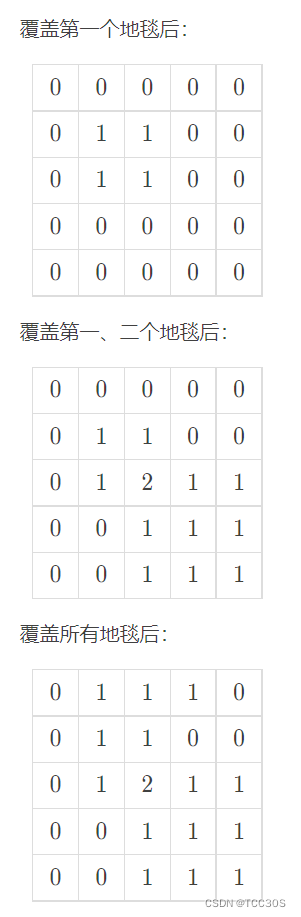
差分法介绍:
假设我们现在要给[2,5]这个区间加一。原来的序列是:
0 0 0 0 0 0 0 0
这时候我们在2上面打 +1 标记, 6 上面打 -1 标记。那么现在的序列是:
0 +1 0 0 0 -1 0
#include<iostream>
#include<math.h>
#include<algorithm>
using namespace std;
#define ll long long
int a[1002][1002]={0},flag[1002][1002]={0};
int main()
{
int n,m,x1,y1,x2,y2;
cin>>n>>m;
for(int k=0;k<m;k++)
{
cin>>x1>>y1>>x2>>y2;
for(int i=x1;i<=x2;i++)
{
flag[i][y1]+=1;
flag[i][y2+1]-=1;
}
}
int sum;
for(int i=1;i<=n+1;i++)
{
sum=0;
for(int j=1;j<=n+1;j++)
{
sum+=flag[i][j];
a[i][j]+=sum;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cout<<a[i][j]<<" ";
}
cout<<endl;
}
}




















 820
820

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








