蓝桥赛刷题记录DFS解题套路

DFS解决岛屿淹没问题与小朋友崇拜圈算法

原创已于 2024-05-17 16:09:03 修改 · 117 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#深度优先 #算法

于 2023-04-05 23:16:33 首次发布

刷题专栏收录该内容

4 篇文章

订阅专栏

文章介绍了使用DFS算法解决两个问题：1.全球变暖导致岛屿被淹没，计算完全淹没的岛屿数量；2.根据小朋友的崇拜关系，找出能形成圈的最大人数。代码示例展示了如何应用DFS进行深度优先搜索，并提供了相应的退出条件和状态标记。

DFS解题模板套路，菜鸟看不懂大佬们写的，自己总结的最简单容易理解的模板

1.全球变暖

你有一张某海域 NxNNxN 像素的照片，"."表示海洋、"#"表示陆地，如下所示：

.......

.##....

....##.

..####.

...###.

.......

其中"上下左右"四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

.......

....#..

.......

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入描述

第一行包含一个整数 N\ (1 \leq N \leq 1000)N (1≤N≤1000)。

以下 NN 行 NN 列代表一张海域照片。

照片保证第 1 行、第 1 列、第 NN 行、第 NN 列的像素都是海洋。、

输出一个整数表示答案。

输入输出样例

示例

输入

7
.......
.##....
.##....
....##.
..####.
...###.
.......

输出

解法：

#include <iostream>
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#include<string.h>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<algorithm>

using namespace std;

bool FLAG = 1;//是否被完全淹没

int countnumber(char** g, int n) {
    void dfs(char** g, int i, int j, int n);
    int sum = 0;
    if (n <= 0 || g == NULL) {
        return 0;
    }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            if (g[i][j] == '#') {
                FLAG = 1;//默认完全被淹没
                dfs(g, i, j, n);
                if (FLAG) sum++;
            }
        }
    }
    return sum;
}

void dfs(char** g, int i, int j, int n) {
    if (g == NULL || g[i][j] == '.' || i >= n || j >= n || i < 0 || j < 0|| g[i][j] == '0') {
        return;
    }
     g[i][j] = '0';//区分被淹没和之前就是海洋
     bool flag = 1;//默认不会被淹没
     if (g[i][j] == '.' || g[i + 1][j] == '.' || g[i - 1][j] == '.' || g[i][j + 1] == '.' || g[i][j - 1] == '.') {//只要用一边接触到了海洋就会被淹没
         flag = 0;
     }
     if (flag) FLAG = 0;//该岛没有完全被淹没
    dfs(g, i - 1, j, n);
    dfs(g, i + 1, j, n);
    dfs(g, i, j - 1, n);
    dfs(g, i, j + 1, n);
}



int main()
{
    int countnumber(char** g, int n);
    void dfs(char** g, int i, int j, int n);
    int n;
    cin >> n;
    char** g = new char* [n];
    for (int i = 0; i < n; i++)
        g[i] = new char[n];
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            cin >> g[i][j];
        }
    }

    cout << countnumber(g, n);

    return 0;
}

2.小朋友崇拜圈

题目描述

班里 NN 个小朋友，每个人都有自己最崇拜的一个小朋友（也可以是自己）。

在一个游戏中，需要小朋友坐一个圈，每个小朋友都有自己最崇拜的小朋友在他的右手边。

求满足条件的圈最大多少人？

小朋友编号为 1,2,3,\cdots N1,2,3,⋯N。

输入描述

输入第一行，一个整数 N（3<N<10^5）N（3<N<105）。

接下来一行 NN 个整数，由空格分开。

输出描述

要求输出一个整数，表示满足条件的最大圈的人数。

输入输出样例

示例

输入

9
3 4 2 5 3 8 4 6 9

输出

样例解释

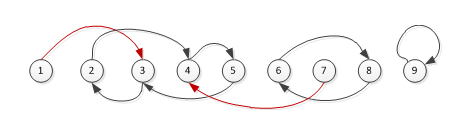
如下图所示，崇拜关系用箭头表示，红色表示不在圈中。

显然，最大圈是[2 4 5 3] 构成的圈。

dfs在这里的用法，肯定就是贪心，一直走一直走，关键是退出条件是，回到起始点。

//举个栗子，1->3->2->4->5->3,这里的回路是2,3,4,5组成，不包含1
//第一遍遍历是1,2,3,4,5的数组设置为-1，-1，-1，-1，-1，代表访问过
//重回3时，将3设置为0,代表这是第二遍访问3了
//不断回退，第二遍访问5,4,2，都设置为0，此时数组为-1,0,0,0,0
//又退回3，这时就是第三遍访问3，g[3]=0，设置flag=1，说明有回路
//不能再退，这时还剩1，直接退出dfs函数

#include <iostream>
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<math.h>
#include<string.h>
#include<vector>
#include<string>
#include<queue>
#include<stack>
#include<algorithm>

using namespace std;


int sum = 0;//成环元素总数
bool FLAG = 0;//是否能够成环，默认不能

int countnumber(int* g, int n) {
    void dfs(int* g, int i, int n);
    int max = 0;
    if (n <= 0 || g == NULL) {
        return 0;
    }
    for (int i = 1; i <= n; i++) {
        if (g[i] != -1 && g[i]!=0) {//0是成环元素，-1是已经访问过，但是没有成环的元素
            dfs(g, i, n);
             if (sum+1 > max) {//+1是因为环内最后一个元素没有进入计算
                max = sum+1;
             }
        }
        FLAG = 0;//当一个环结束后，重置
        sum = 0;
    }
    return max;
}

void dfs(int* g, int i, int n) {
    if (g == NULL || g[i] == i || i > n || i < 0 || g[i] == -1) {
        if (g[i] == -1) g[i] = 0; //相当于第二次访问该元素，说明有一条回路又回到该元素
        return;
    }
    int a = g[i];
    g[i] = -1;
     dfs(g, a, n);
     if (g[i] != 0 && FLAG==0) {//回退，退到最后一个元素则FLAG=1
         g[i] = 0;
         sum++;
     }
     else {
         FLAG = 1;
     }
}
//举个栗子，1->3->2->4->5->3,这里的回路是2,3,4,5组成，不包含1
//第一遍遍历是1,2,3,4,5的数组设置为-1，-1，-1，-1，-1
//重回3时，将3设置为0,代表这是第二遍访问3了
//不断回退，第二遍访问5,4,2，都设置为0，此时数组为-1,0,0,0,0
//又退回3，这时就是第三遍访问3，g[3]=0，设置flag=1，说明有回路
//不能再退，这时还剩1，直接退出dfs函数


int main()
{
    int n;
    cin >> n;
    int* g = new int[n+1];
    g[0] = -2;//方便起见，数组从下标1开始
    for (int i = 1; i <= n; i++) {
        cin >> g[i];
    }


    cout << countnumber(g, n);

    return 0;
}