课后自主练习（DP）1064. 计算多项式的系数 hard《编程思维与实践》个人学习笔记-优快云博客

这篇博客介绍了一个计算模10007的多项式系数的方法，利用了模运算的性质和杨辉三角的递推公式。通过递归填充杨辉三角矩阵，并在每一步都进行模运算，最终得到指定位置的系数。代码示例展示了如何实现这一过程。

题目

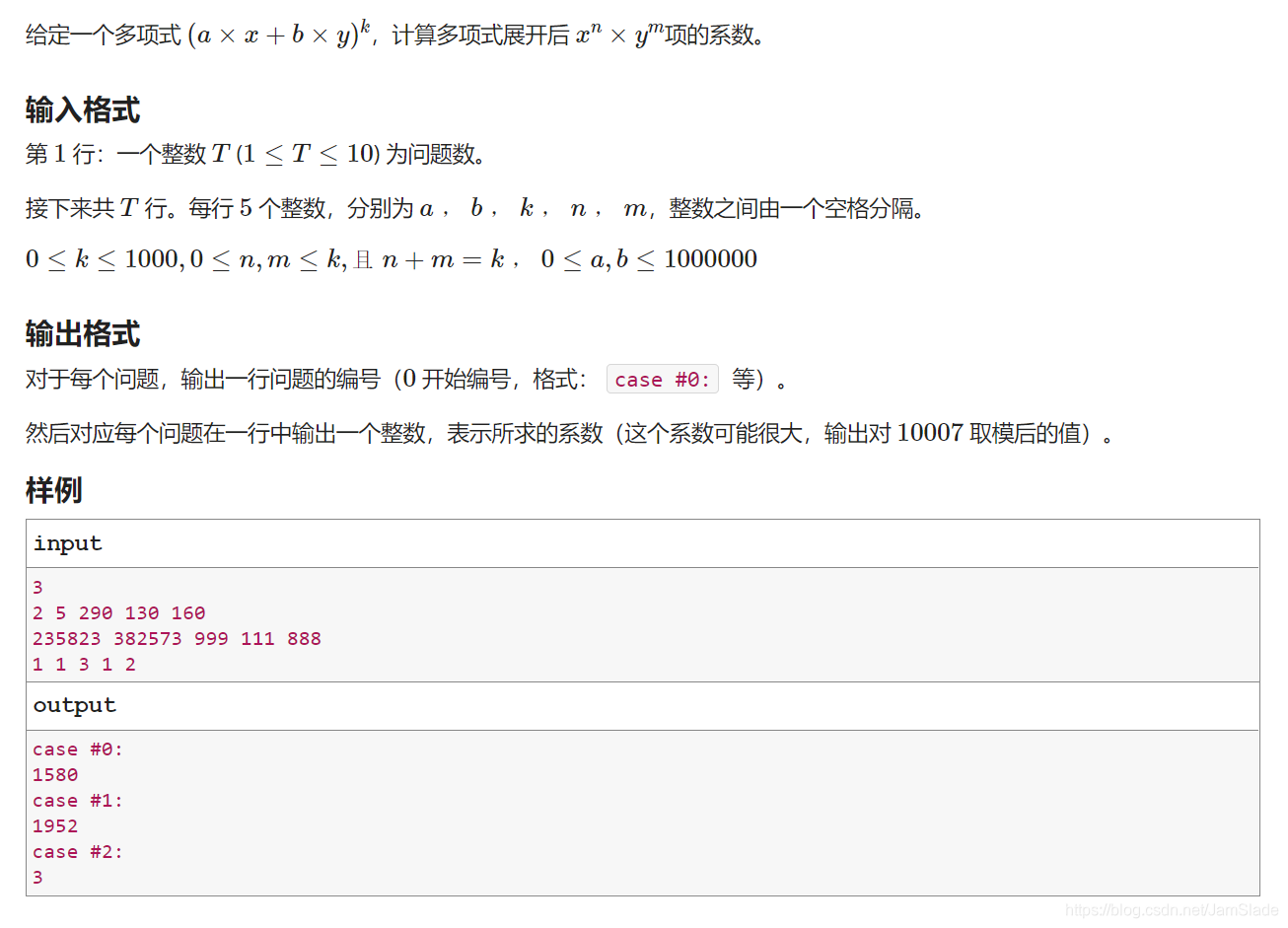
在这里插入图片描述
数据
3
2 5 290 130 160
235823 382573 999 111 888
1 1 3 1 2

思路

①这题目略坑，说要输出一个mod10007的数字
那么我们有一个mod的性质 $(a+b)%10007==(a%10007+b%10007)%10007(a+b)\%10007 == (a\%10007 +b\%10007)\% 10007$
$(a×b)%10007==(a%10007×b%10007)%10007(a×b)\%10007 == (a\%10007 ×b\%10007)\%10007$
所以在递推的时候注意每次都mod10007即可

②递推思路

在这里插入图片描述
不难发现，求多项式系数的本质就是杨辉三角
$f (n, m) = a \times f (n - 1, m) + b \times f (n, m - 1)$

或者用组合数递推也可以，这里不再赘述

代码

#include<iostream>
#define ll long long

using namespace std;

ll arr[2000][2000];


int main()
{
    ll t;
    cin >> t;
    for(ll i = 0; i < t; i++)
    {
        ll a,b,k,n,m;
        cin >> a >> b >> k >> n >> m;

        a %= 10007;
        b %= 10007;
        
        arr[0][0] = 1;
        for(ll i = 1; i <= k; i++)
        {
            arr[i][0] = arr[i - 1][0] * a % 10007;
        }
        for(ll i = 1; i <= k; i++)
        {
            arr[0][i] = arr[0][i - 1] * b % 10007;
        }

        for(ll i = 1; i <= k; i++)
        {
            for(ll j = 1; j <= k; j++)
            {
                arr[i][j] = (a * arr[i - 1][j] + b * arr[i][j - 1]) % 10007;
                //斜着看就是杨辉三角了
            }
        }
        cout << "case #" << i << ":"<<endl;
        cout << arr[n][m] << endl;
    }

    return 0;
}