排序专题(6)——堆排序

算法说明

堆排序与之前的排序算法不同，它建立在树结构的基础之上。

堆排序就是一个构建堆的过程(所谓堆就是一个二叉树)，当按照升序排序时，构建大根堆；降序排序时，构建小根堆。

堆类型	说明
大根堆	让当前数组中最大的元素在堆顶也就是作为根节点，对于每个有左右子节点的节点而言，其左右子节点的值也都小于其值。
小根堆	与大根堆相反。

以序列：50 10 90 30 70 40 80 60 20为例。其构建的初始堆如图，生成大根堆的过程，

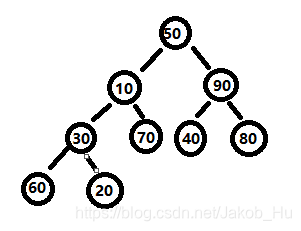
根据二叉树的性质，有n个节点的完全二叉树，其含有子节点的节点个数是n/2个。故从 9//2=4 的节点(也就是30对应的节点)开始，构建大顶堆。30的子节点是60和20，其中60>30，二者进行交换操作，堆结构变化为，

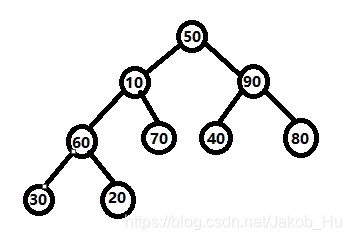
接第3个节点(即90对应的节点)，其值大于子节点的值，不发生改变。

之后是10对应的节点，10<60 && 10<70，选子节点中的大者进行交换，如下图，

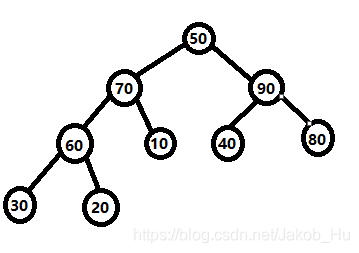
最后是根节点50，其小于左右子节点，调大者进行交换，

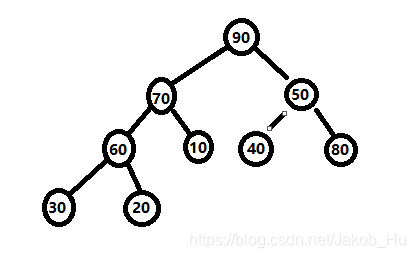
注意此时构建的堆中，最大值90位于根节点。符合小根堆的情况。

如果是升序排列，需要生成大根堆，则需要和堆末尾元素交换。得到如图，

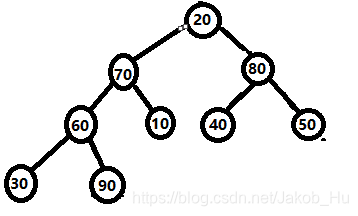
无论是大根堆还是小根堆，此后的排序完全可以忽略末尾元素，因为已经就位了，剩下的元素排序过程同上，也是先构建堆然后交换堆顶，直到剩下最后一个元素为止。

算法实现

实现序列的升序排列，

def heap_sort(alist):
	n = len(alist)
	i = n // 2
	# 进行 n-1次排序
	while i >= 0:
		heap_adjuest(alist, i, n-1)
		i -= 1
	for i in range(n-1, 0, -1):
		temp = alist[i]
		alist[0] = alist[i]
		alist[i] = temp
		heap_adjust(alist, i-1)

def heap_adjust(alist, start, end):
	"""构建大根堆"""
	temp = alist[start]
	i = 2 * start + 1
	while i < end:
		if i + 1 < m and alist[i] < alist[i+1]:
			i = (i + 1) * 2
		if temp >= alist[i]:
			break
		alist[start] = alist[i]
		s = i
	alist[start] = temp
	

算法时间复杂度和稳定性

堆排序最好和最坏的时间复杂度都是 O(nlogn)，不具稳定性。