一,随机试验与随机事件
1.随机试验的特点
(1)可重复性
(2)多结果性
(3)不确定性
2.样本空间:
(1)样本空间:随机试验的所可能的结果的集合,Ω
(2)样本点:每一种可能的结果,
3.事件
(1)基本事件:不能再细分的事件,只有单个样本点
(2)随机事件:样本空间的一个子集
(3)不可能事件:不含任何样本点,
(4)必然事件:含全部的样本点,Ω
4.事件的运算
(1)包含:A
B,A发生,则B必然发生
(2)并(和):A
B,A,B至少有一个发生,记为A+B
(3)交(积):A
B,A,B同时发生,记为AB
(4)差:A-B,A发生而B不发生
(5)互不相容(互斥):AB=
,多个事件
(6)对立:A+B=Ω,AB=
,A的对立事件B记作
,两个事件
(7)完备事件组A1,A2,A3,......,An,满足Ai∩Aj=
,且
Ai=Ω
5.
事件的运算律
(1)交换律:A∩B=B∩A,A∪B=B∪A
(2)结合律:(A∪B)∪C=A∪(B∪C),(A∩B)∩C=A∩(B∩C)
(3)分配律:(A∩B)∪C=(A∪C)∩(B∪C),(A∪B)∩C=(A∩C)∪(B∩C)
(4)对偶率:
二,频率与概率
1.概率的性质
(1)非负性
(2)规范性
(3)可列可加性
(4)概率为0的事件也可能发生
(5)有限可加性
2.概率公式
(1)加法公式
A,B互不相容,则P(A+B)=P(A)+P(B)
反之,P(A+B)=P(A)+P(B)-P(AB)
(2)减法公式
P(
)=1-P(A)
(3)减法公式
A
B,则P(A-B)=P(A)-P(B),且P(A)
P(B)
推论:对任意事件A,B有P(A-B)=P(A)-P(AB)
(4)P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
三,古典概型和几何概型
1.古典概型
(1)有限个样本点
(2)等可能性
2.几何概型
四,条件概率与乘法公式
1.条件概率
(1)条件概率的样本空间发生了改变
(2)A,B两事件,P(A)>0,在A已经发生的条件下,B发生的概率称为B对A的条件概率,记作P(B|A)
2.条件概率的公理
(1)非负性
(2)规范性
(3)可列可加性
3.乘法公式
(1)P(B|A)=P(AB)/P(A),P(A)>0
(2)P(A|B=P(AB)/P(B),P(B)>0
(3)P(ABC)=P(A)P(B|A)P(C|AB)








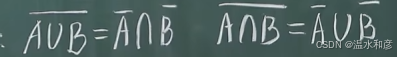

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








