Part2-Chapter8-预测数值型数据：回归-原理

回归的目的是通过计算来预测数值型数据，本章讨论的是线性回归和局部加权回归。这两种方法由三部分构成：数据矩阵X和结果矩阵Y：

回归系数矩阵：

结果矩阵：

对线性回归，找出w的方法是，找到一个w，使得预测结果u与真实结果y的差值最小。因为差值有正 有负，因此我们用平方和最小的方式：

用矩阵表示为：

求其最小值，则对其求导，并令结果为0，推出：

绘制结果为：

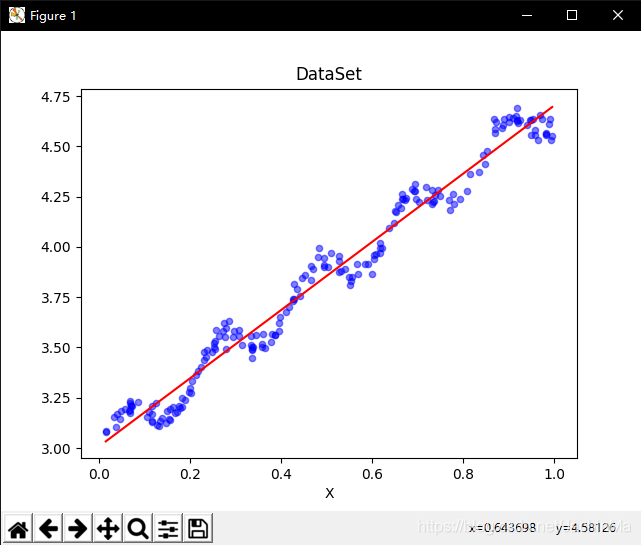
蓝色为数据点，红线为预测回归方程。

因为线性回归要求误差方差最小，因此当模型本身欠拟合时，预测结果将不能很好地符合实际。因此我们有时候允许估计有一定的误差，从而得到更好的预测结果。其中的一个方法是局部加权线性回归。在该方法中，我们给待预测点附近的每个点赋予一定的权重。与kNN一样，这种算法每次预测均需要事先选取出对应的数据子集。该算法解出回归系数W的形式如下：

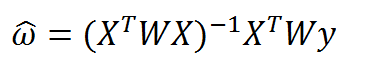
这里的W和w不同，是用来给待测点附近的点赋予权重。计算W的方法很多，但最常用的是高斯核，即：

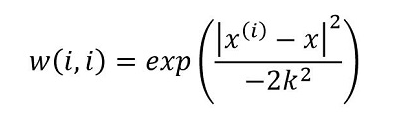
最终结果为：

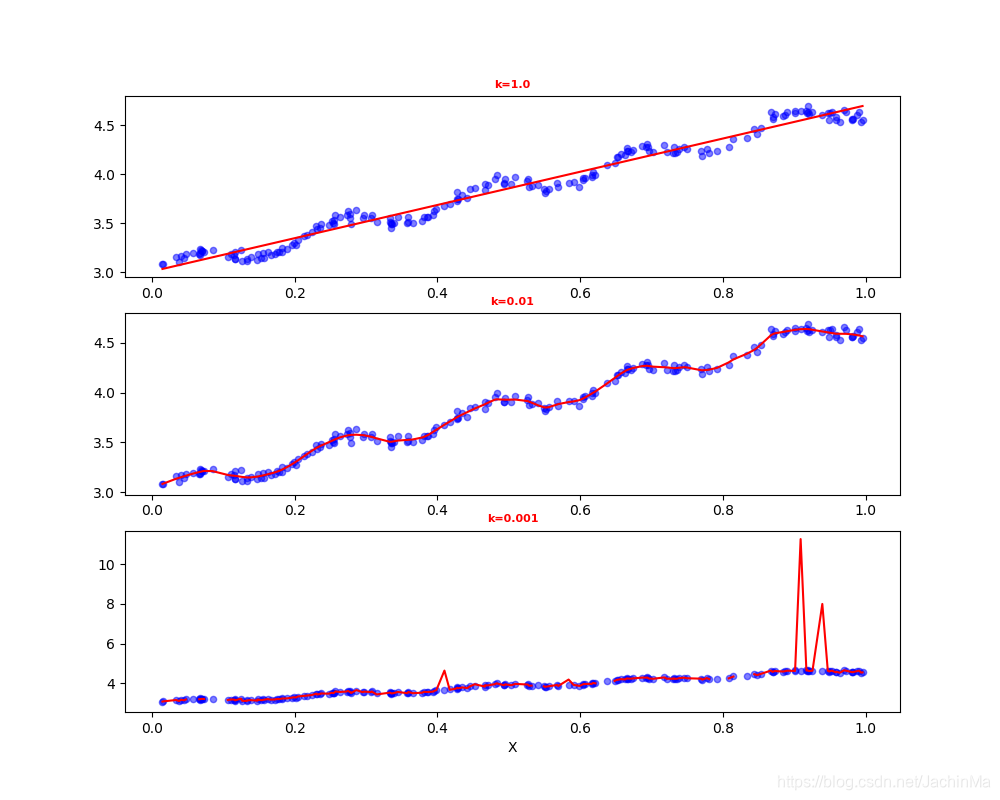
可以看出，k=1时和线性回归一致；k=0.01时有很好的拟合性；而k=0.001时则出现了严重的过拟合现象。