提示:从今天开始讲解数据结构 图相关的知识
图概念的引入
图是一种比线性表和树更加复杂的数据结构。
在线性表中,数据元素之间呈现一种线性关系,即每个元素只有一个直接前驱和一个直接后继;
在树结构中,结点之间是一种层次关系,即每个结点只有一个直接前驱,但可有多个直接后继;
在图结构中,每个结点既可以有多个直接前驱,也可以有多个直接后继。
图概念的实例
在实际生活中,有许多应用问题都可以归结为图的问题。那么什么是图呢?简单地说,图是一个由点及点之间的连线组成的集合。
示例:交通旅游中,城市和城市间距离的信息就可以使用一个图来描述
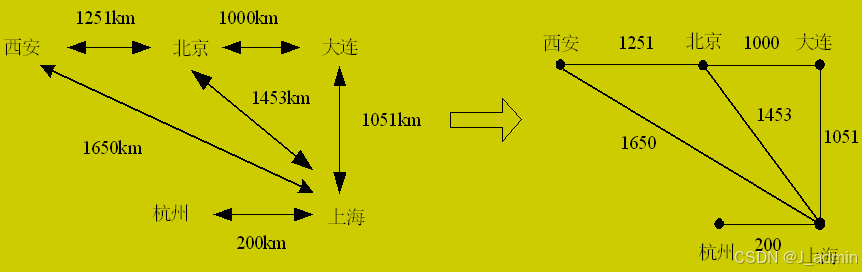
图的定义
图的定义
图(Graph)是由顶点和边组成的,记为G=(V,E),其中V是顶点的非空有穷集合,E是用顶点对表示的边的有穷集合。
无向图: 若图G中表示边的顶点对是无序的,则称G为无向图。
通常用(vi,vj)表示顶点vi和vj间相连的边。在无向图中,(vi,vj)和(vj ,vi)表示同一条边。
如图所示:
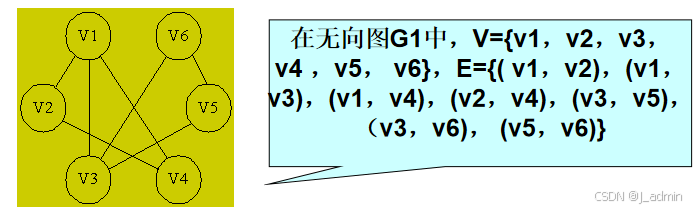
有向图:若图G中表示边的顶点对是有序的,则称G为有向图。有向边通常称为弧;
用<vi,vj>表示从顶点vi到顶点vj 的一条弧,并称vi为弧尾(或初始点),称vj为弧头(或终端点)。在有向图中,〈vi,vj〉和〈vj ,vi〉表示两条不同的弧。
如图所示:
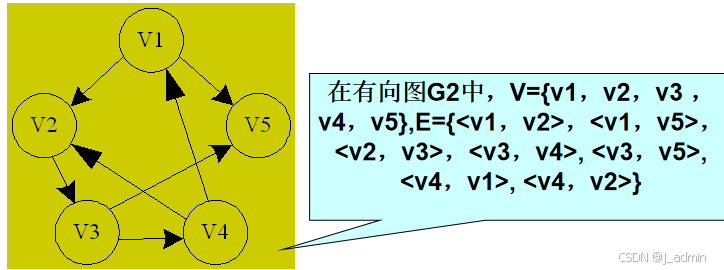
图的基本术语
邻接点、相关边
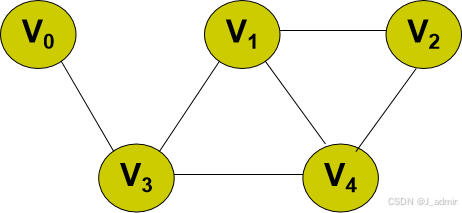
对于无向图G =(V,E),若边(vi,vj)∈E,则称vi和vj互为邻接点,即vi和vj相邻接,而边(vi,vj)则是与顶点vi和vj相关联的边。
例如: 下图中,与v2相关联的边有(v1,v2)和(v2,v4)。 v1,v2互为邻接点, v2,v4互为邻接点。
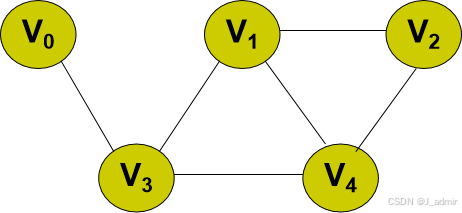
对于有向图G=(V,A),若弧〈vi,vj〉∈A,则称顶点vi邻接到顶点vj,顶点vj邻接顶点vi,而弧<vi,vj>和顶点vi、vj相关联。
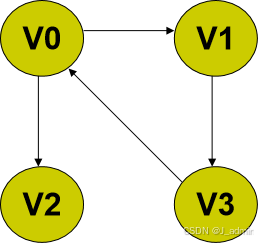
例如:在下图中,v3邻接到v0, v0邻接v3。而与v3相关联的弧有<v1,v3>和<v3,v0>。
完全图
在无向图中,若每对顶点之间都连有一条边,则称该图为无向完全图,因此有n个顶点的完全无向图的边数为n(n-1)/2。
同理可知,具有n(n-1)条弧的有向图称为有向完全图。
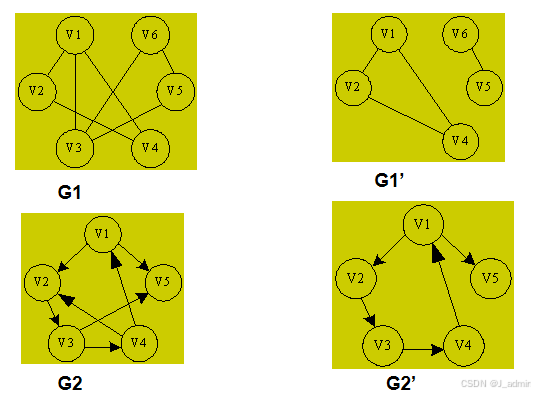
子图
对于图G=(V,E),G’=(V’,E’),若有V’∈V,E’∈E,则称图G’是G的子图。
顶点的度
顶点的度:是图中和vi相关联的边的数目,记为TD(vi)。
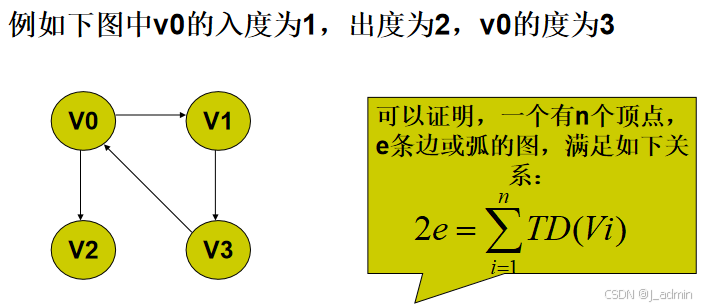
例如 无向图中v0的度为1,v3的度为3,V1的度为3。
在有向图 中,要区别顶点的入度和出度的概念。
顶点vi的入度:是指以vi为头的弧的数目;
顶点vi的出度:是指以vi 为尾的弧的数目,
所以顶点vi的度TD(vi)=入度(vi)+出度(vi)。
附赠练习题
在一个图中,所有顶点的度数之和等于所有边数的()倍。
(A)1/2(B)1(C)2(D)4
在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的()倍。
(A)1/2(B)1(C)2(D)4
路径、回路
无向图G=(V,E)中,从顶点v到顶点v‘间的路径是一个顶点序列(v= vi0,,vi1,vi2,...,vim =v’)
若是有向图,则路径也是有向的。路径上边或弧的数目称为 路径长度。如果路径的起点和终点相同(即v=v’),则称此路径为 回路或环。序列中顶点不重复出现的路径称为 简单路径。
连通的概念
若从顶点vi到顶点vj有路径,则称vi和vj是连通的。
如果无向图中任意两个顶点vi和vj(i≠j)都是连通的,则称该无向图是连通图。
无向图中极大连通子图 称为连通分量。
连通图中的极大连通子图就是其本身。非连通图中有多个。
对于非连通图:不连通的无向图又可以分为若干个连通子图,其中有这样的连通子图,它包含了图中尽可能多的顶点以及尽可能多的边,以至于它再加上一个点或者边之后它就不连通了,此时这个图就是极大连通子图。
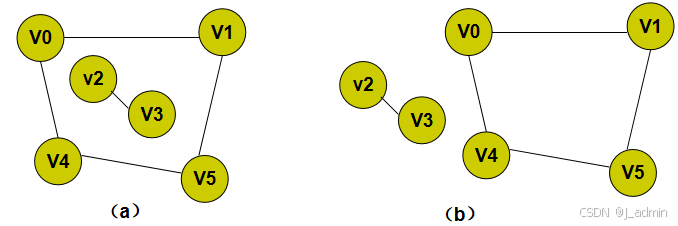
图(a)中的G3是一个非连通图,它有两个连通分量,见图 (b)。
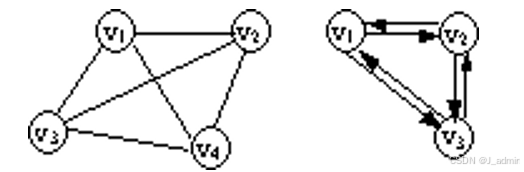
强连通
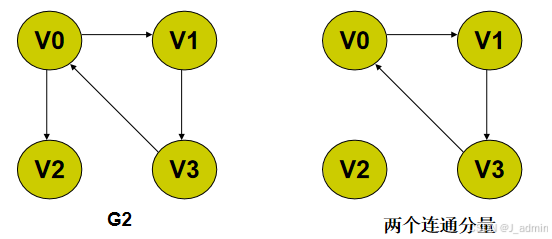
在有向图中,若任意两个顶点vi和vj都连通,即从vi到vj和从vj到vi都有路径,则称该有向图为强连通图。有向图中的极大强连通子图称为该有向图的强连通分量。图中的G2 不是强连通图,但它有两个强连通分量,见下图。
权、网
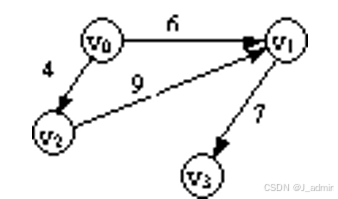
在一个图的每条边或弧上,有时可以标上具有某种含义的数值,这种与图的边相关的数值称为权(Weight)。这种边或弧上带权的图称为网(Network)。下图所示的就是一个网。
附赠练习题
一个有n个顶点的无向图最多有()条边。
(A)n
(B)n(n-1)
(C)n(n-1)/2
(D)2n
具有6个顶点的无向图至少应有()条边才能确保是一个连通图。
(A)5(B)6(C)7(D)8
在一个具有n个顶点的无向图中,要连通全部顶点至少需要()条边。
(A)n (B)n+1(C)n-1(D)n/2

(1) 该图是强连通的吗? 若不是,则给出其强连通分量。
(2)请给出每个顶点的度,入度和出度。





















 388
388

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








