密码学基础（一）——古典密码

保密是密码学的核心。密码学的基本目的是面对攻击者Oscar，在被称为Alice和Bob的通信双方之间应用不安全的信道进行通信时，设法保证通信安全。密码学研究对通信双方要传输的信息进行何种保密变换以防止未被授权的第三方对信息的窃取。此外，密码技术还可以用来进行信息鉴别、数据完整性检验、数字签名等。

首先介绍几个基础的定义：

M:明文消息空间，表示所有可能的明文组成的有限集。

C：密文消息空间，表示所有可能的密文组成的有限集。

K：密钥空间，表示所有可能的密钥组成的有限集。

E：加密算法集合。

D:解密算法集合。

需注意加密函数ekey必须是一个一一映射，否则在解密过程午饭准确确定密文y对应的明文x。

下面介绍几种古典密码体制：

 

 

 

• 棋盘密码

在网上找了个大概的图片，用横纵两个数字去表示一个英文的字母，例如明文hello，密文应为：23 15 31 31 34。同理根据密文结合棋盘对应横纵坐标可以知道所对应的英文字母进而进行解密。

 

• 移位密码（凯撒密码）

移位密码还有一个更耳熟能详的名字叫做凯撒密码，就是将26个英文字母进行移位组成密文。定义为：

ekey(x)=(x+key)mod26

dkey(x)=(y-key)mod26

 

• 代换密码

26个英文字母和Z26的元素之间可以建立一个一一对应关系。例如：a->q,b->w，则明文ab对应密文为qw。

前面介绍的密码为单表代换密码，下面介绍一种多表代换密码。

 

• 维吉尼亚密码

 

• 仿射密码

仿射密码的核心就是设置k1,k2,其中k1要和26互质，加密过程为e=（k1x+k2）mod26，解密为d=k1的互质元素*(y-k2)mod26，假设k==(11,3),密文为13，则y=(11*13+3)mod26=16，解密的公式为x=19*(16-3)mod26=13。（11与26的互素元素为19）

• 置换密码

置换密码其实说来简单，简言之就是明文是ab,密文可以讲第一个第二个字母互换，密文为ba，解密时按照加密规则再次置换回去即可。

• Hill密码

Hill密码同样体现的是“分组-置换”的规则。只是置换时按照矩阵的方式进行运算。

假设密钥为m*m的矩阵A,，则其对应的逆矩阵为Bmod26

设加密的明文为hill，则对应英文顺序组成的矩阵为C,加密算法为，，结果为D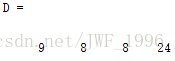，D即为密文，通过D于逆矩阵相乘mod26即可翻译出明文E，翻译结果为hill。