矩阵的平移及旋转--再论《求二个圆的交点》

其实，二个圆的交点问题的背景是：全站仪后方交汇法自动设站的原理。这里直接简化为：已知二个圆的圆心坐标和半径（x1,y1）r1 和（x2,y2）r2 ，求它们的交点。之前从圆的一般方程入手，联立两个圆的方程求解交点：详见之前的日志《求两个圆的交点-解析式推导及编程》，总觉表达式较复杂，有没有更简洁的办法。
最近考虑到矩阵的运算，矩阵左乘向量可以对向量进行旋转、平移及拉伸操作，可有具体的实例来演示这种变换？我想到了之前的求两圆交点的问题：若把两个圆心及它们的交点看成一个三角形，首先把这个三角形平移到坐标原点(0,0)，然后底边旋转至与x轴平齐，这时已知三角形的三条边a,b,c 再来求解交点就容易多了~，如下图所示：
图1 已知a,b,c求交点就容易多了

求出交点后再把这个坐标”旋转-平移“回去就好了，”先平移再旋转"可以归结为”旋转矩阵左乘平移矩阵“再乘待变换的点，而变换回去，就是相当于左乘它们的逆矩阵！“完美”~！
请看下面的推导过程。
T1为平移矩阵，a为x方同的平移，b为y方向的位移量，至于为什么多一个1，是为了适应矩阵的乘法需要，谓之这种形式为齐次形式。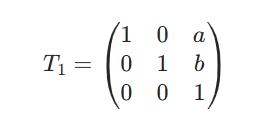
T2为旋转矩阵，同样二维扩展为三维形式，是为了和平移保持一致。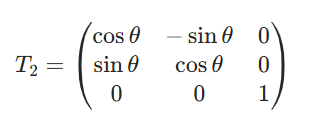
将二者相乘进行复合得到的矩阵M即表示“先平移再旋转”，注意：这个乘法是有顺序讲究的。矩阵的乘法只满足结合律，不满足交换律。

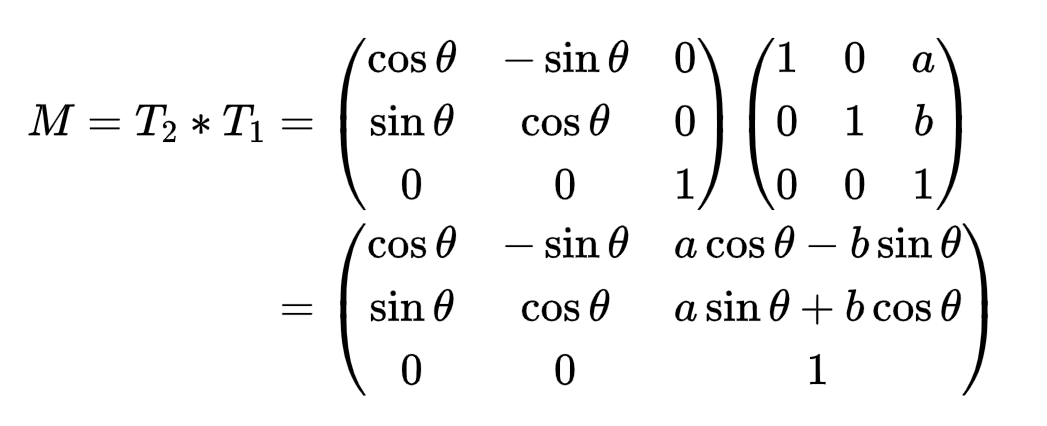
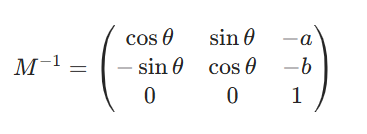
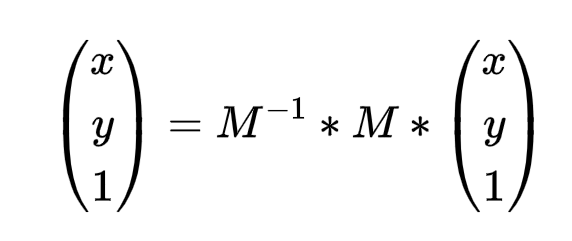
                        图2 平移与旋转矩阵的合成及其逆矩阵

若设平移矩阵为T1,旋转操作的矩阵为T2，则”先平移再旋转“可表达为 T2 * T1 ，注意T2,T1顺序是不能颠倒的，矩阵的乘法不满足交换律，但满足结合律。尤为神奇的是，先平移再旋转的两步操作可以合成一步完成！即事先计算出T=T2 * T1，然后用T乘以（x,y,1）即可。而T1*T2则表示“先旋转再平移”，考虑一下，它与“先平移再旋转“效果并不一样。
假设已经三角形已经平移旋转到位（图1），先计算出交点坐标，然后左乘T的逆矩阵即可旋转平移到原来的坐标！它的逆过程是相反的：先旋转再平移。然而，你不用太担心具体细节，因为这个过程已经自然地包含在T的逆矩阵里了。这就是数学的神奇之处。
下面通过python编程计算，与CAD绘图结果完全相符，证明方法可行，并且正确！

#解三角形,并用矩阵平移旋转2025-4

import math
import numpy as np

PI=math.pi

x1=3263.592;y1=2797.333;r1=152.360
x2=3638.300;y2=2922.089;r2=306.882

a=math.sqrt((x1-x2)**2+(y1-y2)**2)  #底边
b=r1
c=r2
# a,b,c 顺序：a为底边，b为左侧，c为右侧
def TRG(a,b,c)->list:
    if a+b>c and a+c>b and b+c>a and a>0 and b>0 and c>0:
        p=(a+b+c)/2
        s=math.sqrt(p*(p-a)*(p-b)*(p-c)) #海仑公式计算面积
        h=2*s/a                    # 由面积和底边求高h
        x=math.sqrt(b**2-h**2)        
        return [x,h]              # 返回顶点bc交点的 x,y 坐标
    else:
        return [-1,-1]  # 错误 的 三角形
    
JD=TRG(a,b,c)  # 对称交点之一

if JD[0]==-1 and JD[1]==-1:
    print("\n错误~没有交点！")
    exit(0)


#计算与x轴之间的夹角cita
if x2==x1 :
    if y2>y1:
        cita=PI/2
    else:
        cita=3/4*PI
else:
    cita=math.atan((y2-y1)/(x2-x1))
    if x2-x1<0:
        cita=PI+cita
# 下面求变换矩阵
cosa=math.cos(-cita)
sina=math.sin(-cita)
#已将(x1,y1)平移到原点并旋转了-cita角，现在将所求交点再变换回去
#逆变换矩阵中，-a=-1*-1*x1=x1,同理-b也可直接写为y1
M=np.array([[cosa,sina,x1],
            [-sina,cosa,y1],
            [0,0,1]]) 
print("\n")
for i in range(2):   
    XY=np.array([[JD[0]],
                [(-1)**i*JD[1]],  # 对称的2个坐标
                [1]])
    BH=M@XY   #version3.6直接支持矩阵乘法
    x=BH[0][0]
    y=BH[1][0]
    print(f"交点坐标{i+1}:x={x:.3f},y={y:.3f}")
```css

#输出结果：
交点坐标1:x=3331.636,y=2933.655
交点坐标2:x=3399.772,y=2729.006

完美的数学！矩阵的力量！