梯度下降法

1. 前言

无约束优化问题常用的求解算法有梯度下降法（基于迭代）、最小二乘法（基于解析解）、牛顿法&拟牛顿法（基于迭代）。今天先介绍最常用的梯度下降法。

2. 梯度的含义

2.1 导数

正式介绍梯度之前，我们可以先回想一下导数。函数在某一点的导数是指函数在这个点的变化率，几何意义为函数在这个点上的切线的斜率，这个概念大家一定不陌生！（在一元情况下，梯度就是导数）

2.2 偏导数

函数在某一点，关于某个自变量的变化率。

比如函数$f(x,y)$, 分别对$x$,$y$求偏导数为：$\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$。

2.4 梯度

对多元函数的参数求$\partial$偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

比如对于函数$f(x,y)$, 分别对$x$,$y$求偏导数为：$\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$，其梯度向量就是$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$，简称$gradf(x,y)$或者$▽f(x,y)$ 。

梯度的方向代表了函数增加最快的方向，比如对于函数$f(x,y)$来说，它在$(x_0,y_0)$处，沿着梯度方向$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial y_0})$移动就是使得$f(x,y)$增加最快的方向，因此就最快找到函数的最大值。反之，如果我们想找的是函数的最小值，只要沿着梯度相反的方向$(-\frac{\partial f}{\partial x_0},-\frac{\partial f}{\partial y_0})$移动就可以了。

3. 梯度下降法详解

3.1 直观理解

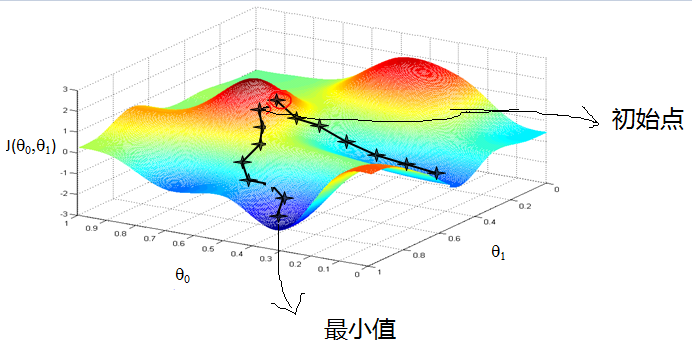
想象我们在一座大山上，由于我们不知道怎么下山，于是只能走一步看一步，也就是每走到一个位置的时候，求解当前位置的梯度，然后沿着负梯度的方向，也就是最陡峭的方向往下走。就这样一直走下去，直到我们觉得来到了山脚下。当然，按照这个方法我们不一定能到达真正的山脚，有可能只是到达了某一个局部的山峰低处。

3.2 基本概念

（1）步长/学习率：每次沿着梯度的方向走的距离，决定在一次学习中，应该学习多少，以及多大程度上更新参数；
（2）特征：样本的输入部分，比如一个单特征样本$(x_0,y_0)$，它的特征就是$x_0$，标签是$y_0$；
（3）假设函数：在监督学习中，为了拟合输入样本和输出值的关系，我们会设置一个假设函数$h_{\theta }(x)$，对于单个特征的$m$个样本$(x_0^i,y_0^i),i=\mathrm{1...}m$，我们可以采用的拟合函数是：$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$$
（4）损失函数：用于评估拟合值和真实label之间差距的效果函数，损失函数越小，则拟合的越好。

3.3 算法流程（代数理解）

（1）确定假设函数和损失函数；

比如对于线性回归，假设函数表示为$h_{\theta }(x_1,x_2,...,x_n)={\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n$，其中${\theta }_n$为模型参数；

损失函数可以表示为：
$$J({\theta }_1,{\theta }_2,...,{\theta }_n)=\frac{1}{2m}\sum _{j=1}^m(h_{\theta }(x_1^j,x_2^j,...,x_n^j)-y_j{)}^2$$

（2）初始化参数；

• 步长$\alpha$：比如1；
• ${\theta }_n$：比如0；
• 终止距离$ϵ$：比如10.

（3）梯度下降法迭代过程

step 1: 计算当前位置，对于${\theta }_i$，其梯度的表达式：

$$\frac{\partial J({\theta }_1,{\theta }_2,...,{\theta }_n)}{\partial {\theta }_i}=\frac{1}{m}\sum _{j=1}^m(h_{\theta }(x_1,x_2,...,x_n)-y_j)x_i$$

step 2: 用步长乘以损失函数的梯度，得到当前位置的下降距离；

即：$$\alpha \ast \frac{\partial J({\theta }_1,{\theta }_2,...,{\theta }_n)}{\partial {\theta }_i}$$

step 3: 判断是否停止迭代；

确认对于所有的${\theta }_i$，其梯度下降的距离是否小于停止距离$ϵ$，如果是，则当前所有的${\theta }_i$为最终参数，否则进入下一步；

step 4：更心所有的${\theta }_i$:
$${\theta }_i={\theta }_i-\alpha \ast \frac{\partial J({\theta }_1,{\theta }_2,...,{\theta }_n)}{\partial {\theta }_i}$$

4. 算法调优

（1）算法参数的调优：步长、终止距离、初始参数的选择；
（2）归一化：让样本数据的大小在同一个维度；常用的方法是对每个特征$x$，求出其期望$\bar{x}$和标准差$std(x)$，然后转化为：
$$\frac{x-\bar{x}}{std(x)}$$

5. 三个基本的梯度下降法

5.1 批量梯度下降法 (Batch Gradient Descent)

每次更新参数时，使用所有样本进行更新，假设我们一共有$m$个样本，则更新公式为：
$$\begin{gathered} {\theta }_i={\theta }_i-\alpha \ast \frac{\partial J({\theta }_1,{\theta }_2,...,{\theta }_n)}{\partial {\theta }_i} \\ ={\theta }_i-\alpha \ast \frac{1}{m}\sum _{j=1}^m(h_{\theta }(x_1^j,x_2^j,...,x_n^j)-y_j)x_i^j \end{gathered}$$

5.2 随机梯度下降法 (Stochastic Gradient Descent)

每次更新参数时，使用单个样本进行更新，假设我们选择第$j$个样本进行更新：
$${\theta }_i={\theta }_i-\alpha \ast (h_{\theta }(x_1^j,x_2^j,...,x_n^j)-y_j)x_i^j$$

随机梯度下降法训练速度更快，但是由于它只是用一个样本决定梯度的方向，很有可能不是朝最优的方向在走，因此不能很快的收敛性。

5.3 小批量梯度下降法 (Mini-batch Gradient Descent)

前面的批量梯度下降法和随机梯度下降法有点像是两个极端，一个用所有的样本来更心参数，一个只随机挑选一个来更新参数，小批量梯度下降法则类似于两者的折中，每次采样选择$n$个样本来迭代，因此，更新的公式为：

$${\theta }_i={\theta }_i-\alpha \ast \frac{1}{n}\sum _{j=1}^n(h_{\theta }(x_1^j,x_2^j,...,x_n^j)-y_j)x_i^j$$

6. 梯度下降法的改进算法

原始的梯度下降法可能存在：在梯度平缓的维度下降缓慢、在梯度险峻的位置抖动很大，容易陷入局部最优等缺点。因此出现了很多改进的梯度下降算法，包括：冲量梯度下降法、 NAG: Nesterov Accelerated Gradient、 AdaGrad、AdaDelta等等。

等后面用到的时候再补充吧！

参考文献

1. 梯度下降小结
2. 梯度下降法的工作原理
3. 机器学习-梯度下降算法原理及公式推导
   
4. 如何直观形象地理解方向导数与梯度以及它们之间的关系？