软件测试——功能测试:边界值测试
边界值分析法是对等价类分析方法的补充,其理论基础是假定大多数的错误是发生在各种输入条件的边界上,如果边界附近的取值不会导致程序出错,那么其他的取值导致程序出错的可能性很小。
边界值分析法的使用条件:
- 输入条件规定了一个值的取值范围或规定了值的个数。
- 输入条件规定了一个有序集合。
边界是指,相当于输入等价类和输出等价类而言,稍高于其边界值及稍低于其边界值的特定情况,如图一个例子:

如:两个变量x1和x2的函数F,若F为实现一个程序,要输入x1和x2就可能存在边界:
比如,在做三角形计算时,要输入三角形的三个边长:A、B和C。 我们应注意到这三个数值应当满足: A>0、B>0、C>0、 A+B>C、A+C>B、B+C>A,才能构成三角形。但如果把六个不等式中的任何一个大于号“>”错写成大于等于号“≥”,那就不能构成三角形。问题常出现在容易被疏忽的边界附近。
边界值的例子:
- 对16-bit 的整数而言32767 和-32768是边界
- 屏幕上光标在最左上、最右下位置
- 报表的第一和最后一行
- 数组元素的第一个和最后一个
- 循环的第0次、第1次和倒数第2次、最后1次
上点:边界上的点。若边界是封闭的,上点就在域内。若边界是开放的,上点就在域外。
离点:离上点最近的一个点。若边界是封闭的,离点就在域外。若边界是开放的,离点就在域内。(上点和离点总有一个在域内,一个在域外)。
内点:域内的任意一个点。

对于这个图来说,上点和内点都是测试内点,离点是测试外点。
边界值分析的操作:
- 边界值分析的基本思想是:使用在最小值、略高于最小值、正常值、略低于最大值和最大值处取输入变量值
- 边界值分析的假设:“单缺陷”假设,即失效极少是由两个(或多个)缺陷的同时发生引起的
- 边界值分析测试用例的获得:只使一个变量取极值,其余变量取正常值
- 对于一个n变量的函数,边界值分析会产生4n+1个测试用例
- 边界值分析也是一种黑盒测试
边界值分析是考虑边界条件而选取的一种功能测试的方法,边界值分析的关注点在于输入空间的边界,以标识测试用例,因为软件错误更可能出现在输入变量的极值附近。
人们长期的测试工作经验得知,大量的错误是发生在输入或输出范围的边界上,而不是在输入范围内部。
因此针对各种边界情况设计测试用例,可以查出更多的错误。
推导:边界值分析的假设:“单缺陷”假设。
方法:如一个n变量函数,使除一个以外的所有变量取正常值,使剩余的那个变量分别取最小值、略高于最小值、正常值、略低于最大值和最大值,对于每个变量都重复进行。
- 一个变量取边界值,其他变量取正常值 即:{a1边界集合} X {a2一个正常值} X {a3一个正常值} X {a4一个正常值}…….共n 个集合。
- | {边界集合} |=4 ,| {一个正常值} |=1, |{a1边界集合} X {a2一个正常值} X {a3一个正常值} X {a4一个正常值}…….|=4 ,共4*n个输入值。
- 最后补上一正常值,所有变量都取正常值 。
- 所以共计4*n+1。
如下图:
- 使用边界值分析方法设计测试用例,首先应确定边界情况。
- 根据边界值集合完成迪卡尔积( “单缺陷”假设)。
强调:边界值分析的假设:“单缺陷”假设。
如两个变量函数F的边界分析测试用例是:
{ <x1nom,x2min>, <x1nom,x2min+>, <x1nom,x2max->, <x1nom,x2max>, <x1min,x2nom>,
<x1min+,x2nom>, <x1max-,x2nom>, <x1max,x2nom>,<x1nom,x2nom> }

注意:
(1) 每个边界都要作为测试条件,边界值分析不是从某等价类中随便挑一个作为代表,而是使这个等价类的每个边界都要作为测试条件。
(2)边界值分析不仅考虑输入条件,还要考虑输出空间产生的测试情况,即从输出空间产生边界值的测试情况来考虑条件。
边界确定的方法:测试临近边界的合法数据,以及刚超过边界的非法数据。
越界测试
(对于最大值)通常简单地加1或很小的数
(对于最小值)通常简单地减1或很小的数
- 测试用例不充分
- 不能发现测试变量之间的依赖关系
- 不考虑含义和性质,没有利用理解和想象
- 只能作为初步测试用例使用
- 边界值测试分析采用了可靠性理论的单缺陷假设,如果被测试程序是多个独立变量的函数,这些变量受物理量的限制。
- 健壮性是指在异常情况下,软件还能正常运行的能力。
- 健壮性有两层含义:
- 容错能力
- 输入错误的数据类型。
- 输入定义域之外的数值。
- 恢复能力
- 系统能否重新运行;
- 有无重要的数据丢失;
- 是否毁坏了其它相关的软件硬件。
- 容错能力
- 对于一个n变量的函数,健壮性分析会产生6n+1个测试用例。
容错性测试通常构造一些不合理的输入来引诱软件出错,例如:
(1)输入错误的数据类型。
(2)输入定义域之外的数值。
恢复测试重点考察一下几项:
(1)系统能否重新运行;
(2)有无重要的数据丢失;
(3)是否毁坏了其它相关的软件硬件。
除了变量的5个边界分析取值还要考虑略超过最大值(max)和略小于最小值(min)时的情况,以两个函数变量为例,如图:

健壮性测试是边界值分析的一种简单扩展。
方法:如一个n变量函数,使除一个以外的所有变量取正常值,使剩余的那个变量取最小值、略高于最小值、正常值、略低于最大值和最大值,超过最大值,略小于最小值,对于每个变量都重复进行。
{min-,min,min+ ,nom,max-,max,max+}
- 健壮性考虑的主要部分是预期输出,而不是输入;
- 健壮性测试的主要价值是观察例外情况的处理;
- 如果采用例外处理选择,则必须进行健壮性测试;
- 边界值分析测试用例是最坏情况测试用例的真子集
- n变量函数的最坏情况测试会产生5的n次方个测试用例
以两个变量函数为例,如图:

最坏情况测试将意味着更大工作量
推导:
- n变量函数的最坏情况测试会产生5的n次方个测试用例
- 定义域的边界 |{边界集合}|=5 { min,min+ ,nom,max-,max }
- 所有变量取边界值集合的迪卡尔积
- | {边界集合} |=5 ,故产生5^n个测试用例
- 而边界值分析只产生4n+1个测试用例
n变量函数的最坏情况测试会产生7的n次方个测试用例

健壮最坏情况测试将意味着更大工作量
推导:
- 定义域的边界 |{边界集合}|=7 {min-,min,min+ ,nom,max-,max,max+}
- 所有变量取边界值集合的迪卡尔积
- | {边界集合} |=7 ,7^n
最坏情况测试用例的归纳模式与边界分析的归纳模式一样,有相同的局限性:
- 测试用例不充分
- 不能发现测试变量之间的依赖关系
- 不考虑含义和性质,没有利用理解和想象
- 只能作为初步测试用例使用
特点:
- 最直观、最不一致、具有高度主观性
- 特殊值测试特别依赖测试人员的能力
- 特殊值测试大概是运用最广泛的一种功能测试,虽然特殊值测试是高度主观性的,但是能更有效地发现缺陷
- 随机测试的基本思想:
- 使用随机数生成器选出测试用例值
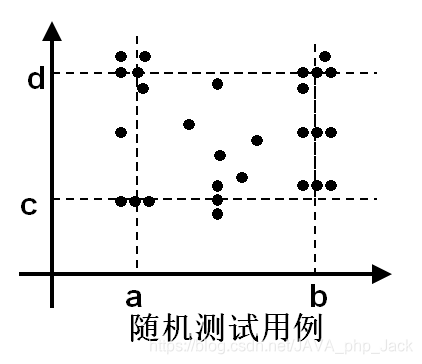
- 使用随机数生成器选出测试用例值
这类测试方法都有一种假设:输入变量的真正独立性(必须保证)
以上介绍的测试方法的区别:
- 正常值与健壮值
- 单缺陷与多缺陷设计
运用好这些差别就能产生较好的测试。

- 如果输入条件规定了值的范围,则应该取刚达到这个范围的边界值,以及刚刚超过这个范围边界的值作为测试输入数据;
- 如果输入条件规定了值的个数,则用最大个数、最小个数、比最大个数多1、比最小个数少1的数做为测试数据;
- 如果程序的规格说明给出的输入域或输出域是有序集合(如有序表、顺序文件等),则应选取集合的第一个和最后一个元素作为测试用例;
- 如果程序用了一个内部结构,应该选取这个内部数据结构的边界值作为测试用例;
- 分析规格说明,找出其他可能的边界条件。





 本文深入探讨边界值分析法,一种补充等价类分析的软件测试方法。通过关注输入条件的边界,该方法能有效发现软件错误,特别是在边界附近。文章详细介绍了边界值分析的原理、操作步骤、假设前提及与其他测试方法的区别。
本文深入探讨边界值分析法,一种补充等价类分析的软件测试方法。通过关注输入条件的边界,该方法能有效发现软件错误,特别是在边界附近。文章详细介绍了边界值分析的原理、操作步骤、假设前提及与其他测试方法的区别。






























 1958
1958

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








