贪心

练习一:加勒比海盗
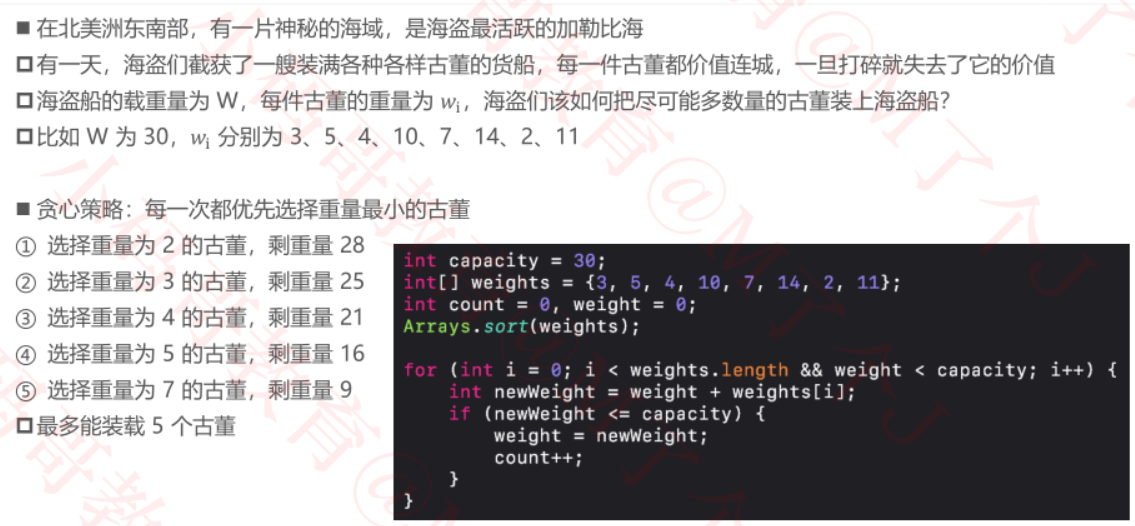
练习二:零钱兑换
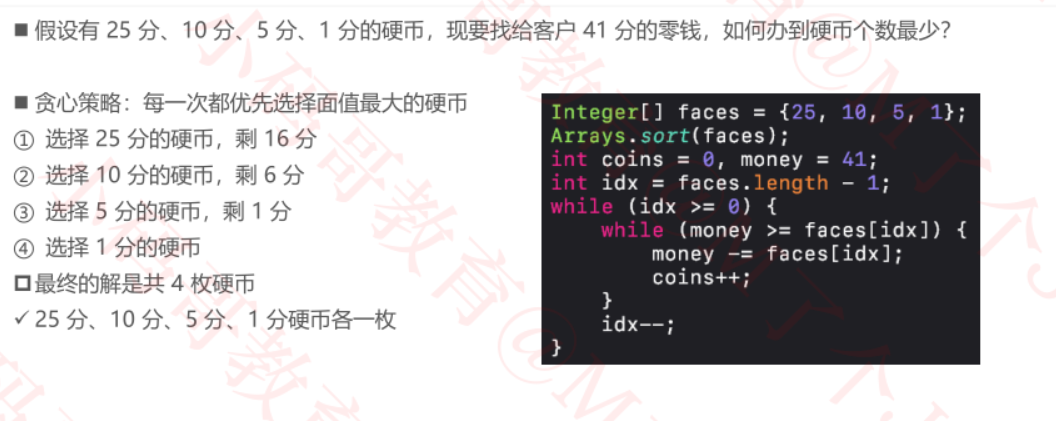

注意

练习三:0-1背包问题

分治
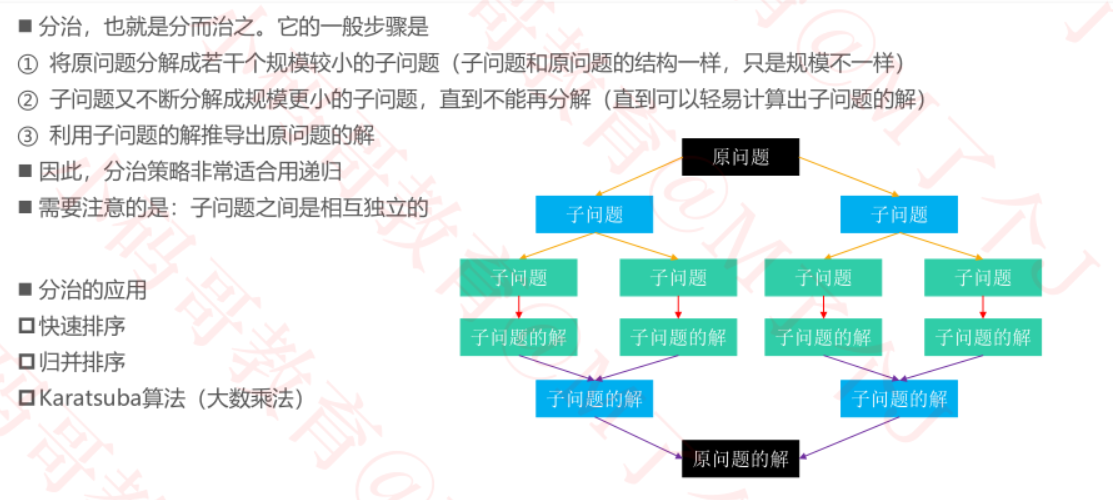
主定理

主定理求时间复杂度,依然利用递归树来推(加点估算),只是还得用对数的一个定理,不是换底公式!
换底公式:

主定理涉及的对数定理:

思考

因为针对具体算法实现时,减少数据量可以使最终操作次数减少。
如:假设对n个数据排序时间复杂度为O(n2),而将n个数据拆成两份,两份各自进行排序,最终时间复杂度为
O(n2 /4) + O(n2 /4) + O(合并消耗的时间)
上述是分治策略最重要的核心,这也是我觉得它与普通递归最大的区别,合并消耗的时间过大的话,分治反而增大了时间复杂度
练习-最大连续子序列和

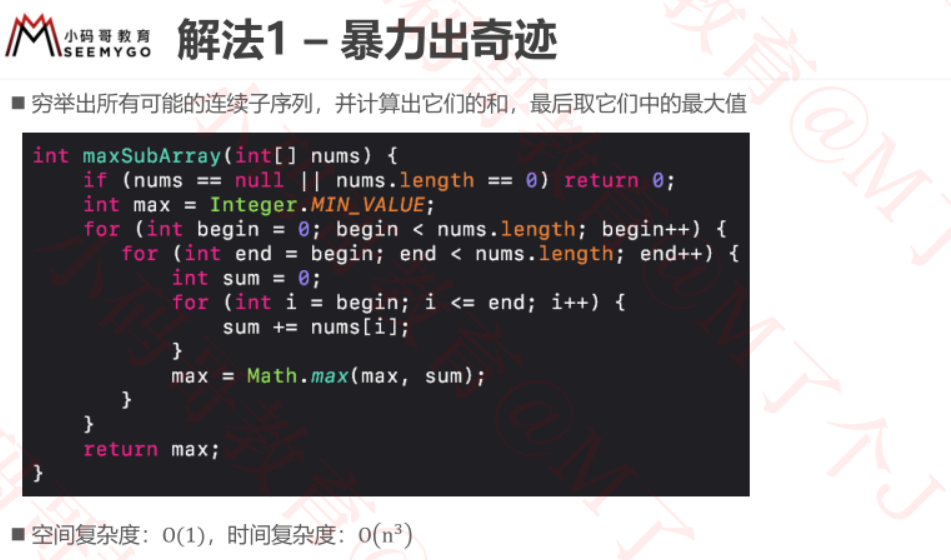


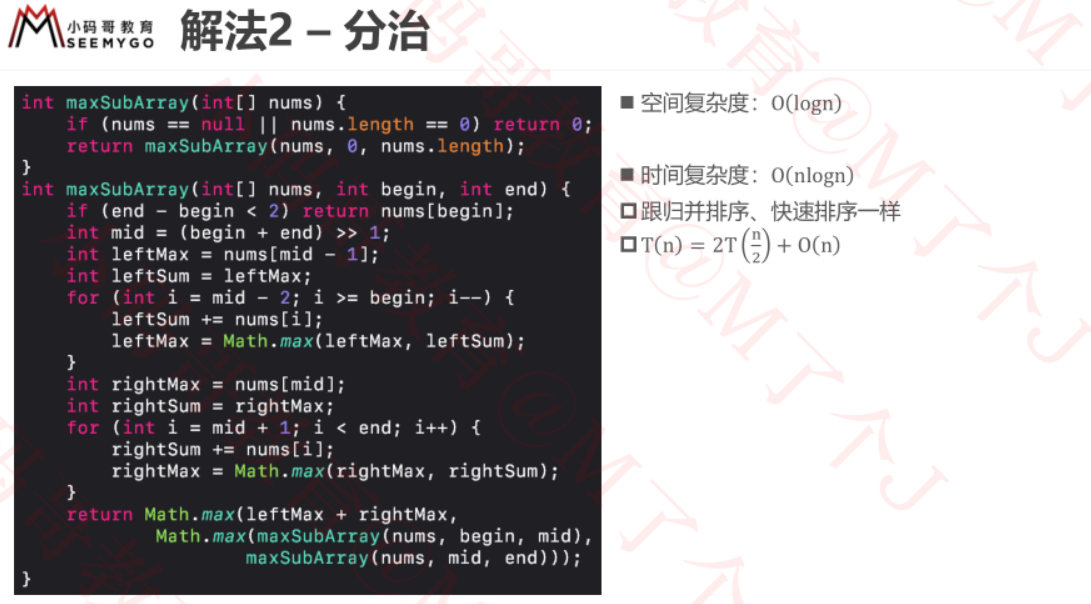
上面那道leetcode题现在如下图:
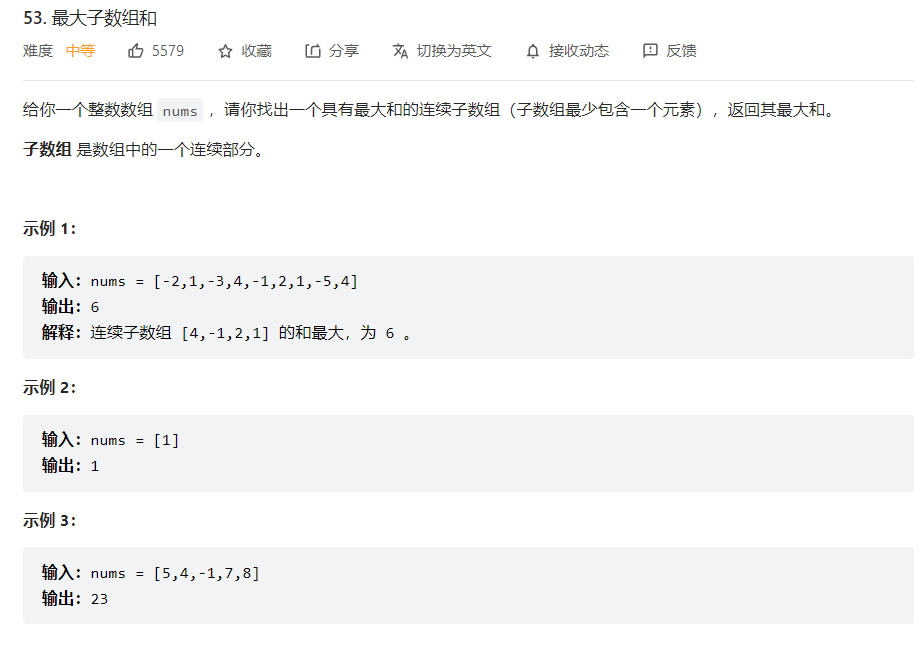
提交的答案:
class Solution {
public class Status{
public int lsum, rsum, isum, msum;
public Status(int lsum, int rsum, int isum, int msum){
this.lsum = lsum;
this.rsum = rsum;
this.msum = msum;
this.isum = isum;
}
}
public int maxSubArray(int[] nums) {
return getInfo(nums, 0, nums.length-1).msum;
}
public Status getInfo(int[] nums, int l, int r){
if(l == r){
return new Status(nums[l], nums[r], nums[l], nums[l]);
}
int m = (l+r)/2;
Status lsub = getInfo(nums, l, m);
Status rsub = getInfo(nums, m+1, r);
return pushUp(lsub, rsub);
}
public Status pushUp(Status l, Status r){
int isum = l.isum + r.isum;
int lsum = Math.max(l.lsum, l.isum + r.lsum);
int rsum = Math.max(r.rsum, r.isum + l.rsum);
int msum = Math.max(Math.max(l.msum, r.msum), l.rsum+r.lsum);
return new Status(lsum, rsum, isum, msum);
}
}
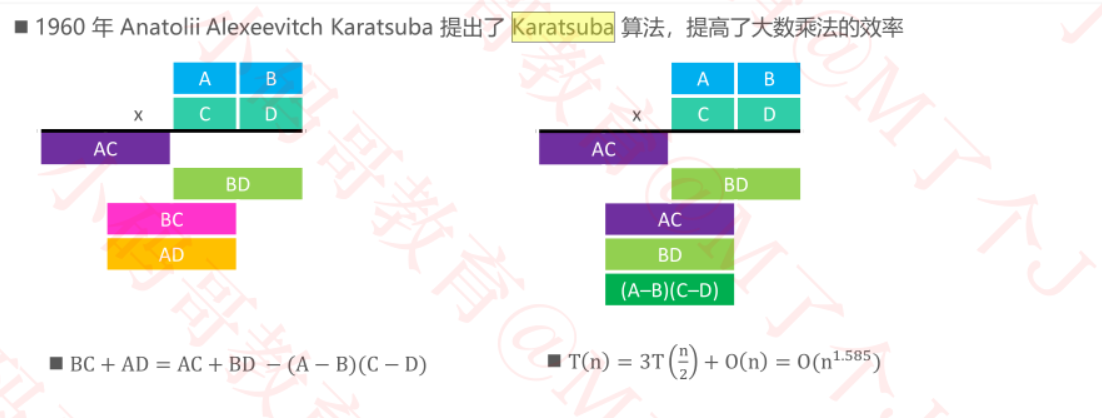
大数乘法 - karatsuba算法

未进行优化时,使用分治法进行大数乘法时间复杂度一样是O(n)
karatsuba算法





 文章探讨了在计算机科学中,如何运用贪心算法解决加勒比海盗和零钱兑换等问题,同时深入讲解了0-1背包问题的分治策略。文中提到了主定理在计算时间复杂度中的应用,并对比了分治与普通递归的区别。此外,还介绍了Karatsuba算法在优化大数乘法过程中的作用,以及未优化时的时间复杂度。
文章探讨了在计算机科学中,如何运用贪心算法解决加勒比海盗和零钱兑换等问题,同时深入讲解了0-1背包问题的分治策略。文中提到了主定理在计算时间复杂度中的应用,并对比了分治与普通递归的区别。此外,还介绍了Karatsuba算法在优化大数乘法过程中的作用,以及未优化时的时间复杂度。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










