Optuna超参数调优图例解读之超参数重要性图

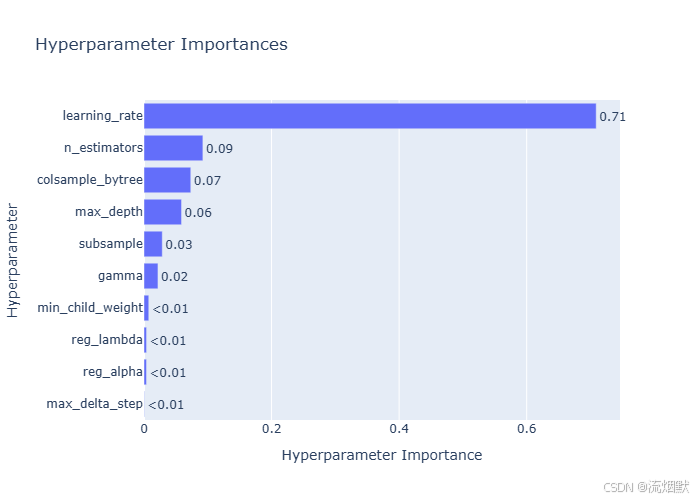
这张图是 超参数重要性图（Hyperparameter Importances），它展示了在你使用 Optuna 或类似工具进行超参数调优时，各个超参数对模型性能的影响程度。

我们来逐项解读：

---

图像概览

• 横轴：Hyperparameter Importance → 超参数的重要性得分（0~1）
• 纵轴：Hyperparameter → 各个超参数名称
• 条形长度表示该参数对最终目标值（如 AUC、准确率等）的影响大小

💡 这些数值通常来自 基于树模型的特征重要性方法（如 XGBoost 的 feature_importance），或者通过 SHAP 值、Permutation Importance 计算得出。

---

逐个分析每个超参数的重要性

超参数	重要性	解读
learning_rate	0.71	最关键！ 学习率决定了每次更新步长，直接影响收敛速度和稳定性。高重要性说明你的模型对学习率非常敏感 —— 太大容易震荡，太小训练慢。
n_estimators	0.09	次要但不可忽视。控制树的数量。虽然不是最核心，但如果设置太少会导致欠拟合，太多可能过拟合。
colsample_bytree	0.07	控制每棵树使用的特征比例。有助于防止过拟合，尤其在特征多时有效。
max_depth	0.06	决定单棵树的最大深度。深度越大越复杂，但也更容易过拟合。
subsample	0.03	控制每棵树使用的样本比例。用于减少方差，提升泛化能力。
gamma	0.02	分割节点所需的最小损失减少量。越大越保守，越不容易分裂。
min_child_weight	<0.01	几乎无影响。控制叶子节点中最小样本权重和。一般用于防止过拟合，但在当前任务中作用很小。
reg_lambda	<0.01	L2 正则化系数。惩罚叶节点权重的平方和。在这里影响极小。
reg_alpha	<0.01	L1 正则化系数。惩罚叶节点权重的绝对值。同样几乎不起作用。
max_delta_step	<0.01	限制叶节点权重变化的最大步长。极少用到，在这里无关紧要。

---

核心结论

最重要的两个超参数是：

1. learning_rate（占比 71%）→ 必须精细调优
2. n_estimators（占比 9%）→ 也需关注

💡 建议：

• 在 Optuna 中优先搜索 learning_rate 的范围（如 0.01~0.3）
• 设置 n_estimators 较大（如 500~1000），然后配合早停机制自动确定最优数量

次要但有用的参数：

• colsample_bytree
• max_depth
• subsample

可以适当调整，但不必过度优化。

几乎可以忽略的参数：

• min_child_weight, reg_lambda, reg_alpha, max_delta_step

这些参数在当前任务中贡献极低，可固定为默认值（如 min_child_weight=1, reg_lambda=0, reg_alpha=0）

---

为什么 learning_rate 如此重要？

因为：

• 它直接控制模型的学习“步幅”
• 如果太大：模型会跳过最优解（震荡不收敛）
• 如果太小：训练太慢，可能陷入局部最优
• 对于梯度提升算法（如 XGBoost），学习率是最关键的“全局调节器”

类比：就像开车时油门踏板 —— 你踩多少，车就走多远。

---

🛠️ 实际建议：如何利用这个结果？

1. 优化策略调整

# 优先搜索 learning_rate
study = optuna.create_study()
study.optimize(objective, n_trials=100)

# 先让 learning_rate 找到好值，再微调其他参数

2. 固定次要参数

# 固定一些影响小的参数
params = {
    'learning_rate': trial.suggest_float('learning_rate', 0.01, 0.3),
    'n_estimators': 1000,
    'max_depth': 6,
    'subsample': 0.8,
    'colsample_bytree': 0.8,
    'min_child_weight': 1,
    'reg_lambda': 0,
    'reg_alpha': 0,
    'max_delta_step': 0
}

3. 简化模型配置

• 不必为每个参数都做网格搜索
• 集中精力调几个关键参数即可

---

总结一句话：

你的模型性能主要由 learning_rate 决定，其次是 n_estimators 和 colsample_bytree；其余参数基本可以忽略。