洛谷P1841 [JSOI2007]重要的城市(Floyd)

题意：

给出n个点(N<=200),m条边的无向图,按从小到大的顺序输出出该图能进行松弛操作的点。

思路：

第一眼看到直接来Floyd暴力，先全部做完，找到松弛完后的最小路径。然后再枚举每一个点，把每一个点依次去掉。如果去掉该点后最短路径长度有变化，那么这一个点就是能进行松弛操作的点(即最重要的城市)。

代码如下(收到大佬Parabola的启发)：

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int e[205][205],d[205][205],m,n,map[205][205];
priority_queue<int> q;
bool check(int x)//判断该点是否为重要的节点
{
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        	map[i][j]=e[i][j];
    for(int k=1;k<=n;k++)
	{
        if(k==x)			continue;//去掉该点
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
	}
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
                if(map[i][j]>d[i][j])
                    return true;
    return false;
}
int main()
{
	scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i!=j)
                e[i][j]=d[i][j]=0x3f;
    for(int i=1,x,y,u;i<=m;i++)		scanf("%d%d%d",&x,&y,&u),e[x][y]=e[y][x]=d[x][y]=d[y][x]=u;
    for(int k=1;k<=n;k++)//先用Floyd做一遍
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
    for(int i=1;i<=n;i++)//枚举每个点
        if(check(i))
            q.push(-i);//用优先队列(但题目要求为从小到大,所以可直接加入它的相反数来解决)
    if(q.empty())					printf("No important cities.");
    else
        while(!q.empty())
            printf("%d ",-q.top()),q.pop();
    return 0;
}

好了，该代码能拿50分。

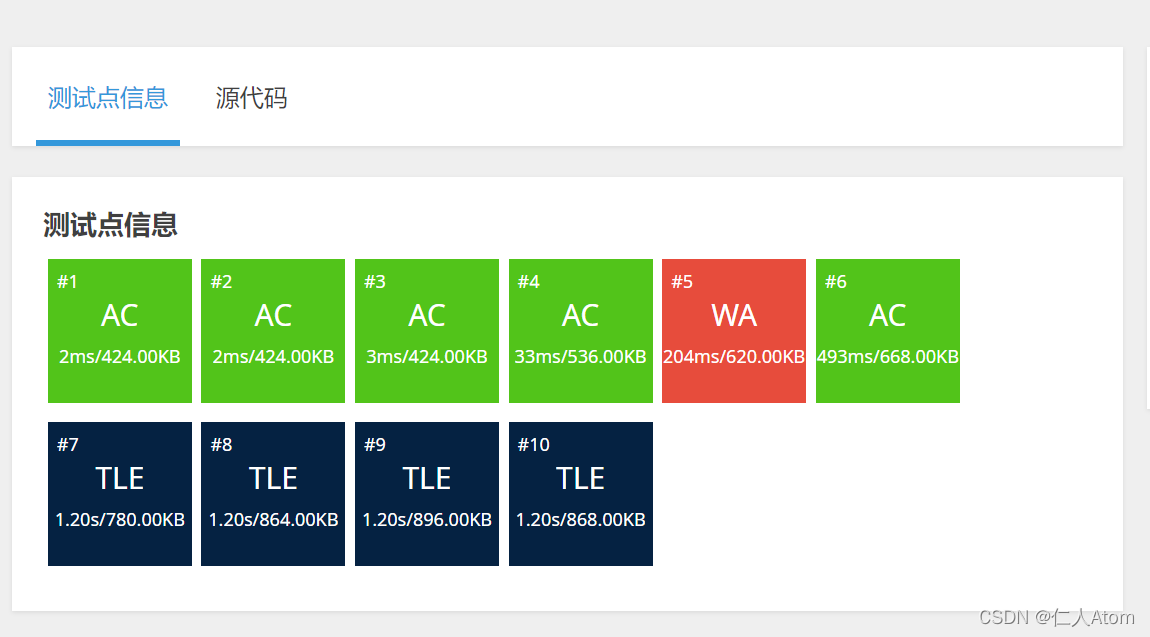
(开了O2可以拿70分)

分析一下程序，大概是O(n^4),但题目中n≤200,爆掉是必然的。

---

能再快一点吗？

好像可以。

把Floyd中不能走的点(即d[i][k]或map[i][k]=∞时)在第二个for循环的时候给剪掉就行了(应该能快一点，但不会太快。期望分70分)

(注意上面的check函数和下面的第一遍Floyd都要剪掉)

代码如下：

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int e[205][205],d[205][205],m,n,map[205][205];priority_queue<int> q;
bool check(int x)
{
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        	map[i][j]=e[i][j];
    for(int k=1;k<=n;k++)
	{
        if(k==x)			continue;
        for(int i=1;i<=n;i++)
    	    if(map[i][k]<0x3f)//剪枝
	            for(int j=1;j<=n;j++)
   					map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
	}
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
                if(map[i][j]>d[i][j])
                    return true;
    return false;
}
int main()
{
	scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(i!=j)
                e[i][j]=d[i][j]=0x3f;
    for(int i=1,x,y,u;i<=m;i++)		scanf("%d%d%d",&x,&y,&u),e[x][y]=e[y][x]=d[x][y]=d[y][x]=u;
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
        	if(d[i][k]<0x3f)//剪枝
            	for(int j=1;j<=n;j++)
                	d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
    for(int i=1;i<=n;i++)
        if(check(i))
            q.push(-i);
    if(q.empty())					printf("No important cities.");
    else
        while(!q.empty())
            printf("%d ",-q.top()),q.pop();
    return 0;
}

 效果不太明显，只多了一个点

---

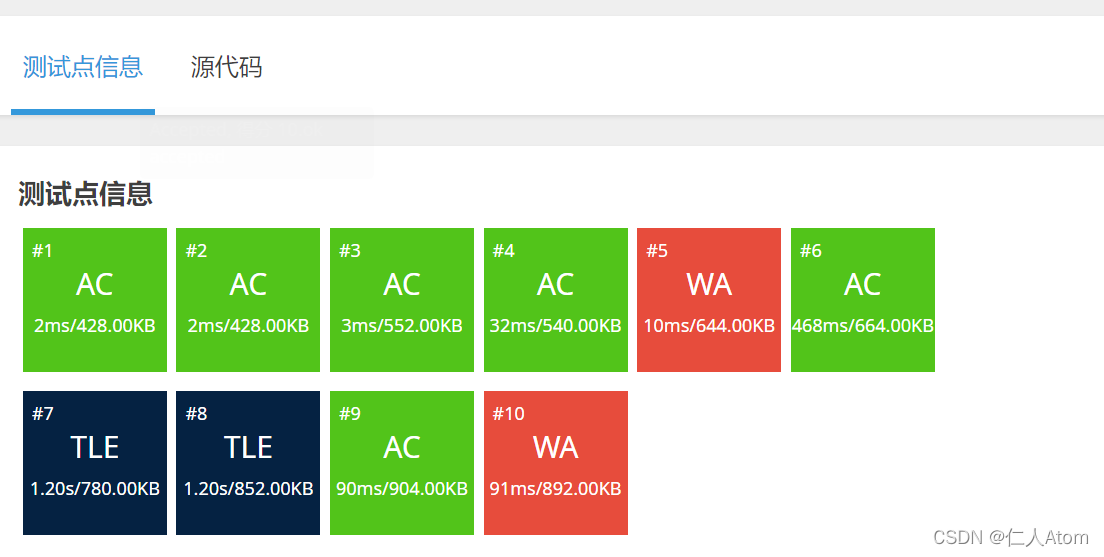
还能再快一点吗？ 

(实在想不出如何改了，换了一下思路)

可以只做一遍Floyd，每一次把松弛的节点记下，最后只做一遍寻找可以松弛的点就好了

见代码

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;
int e[205][205],m,n,map[205][205],p[100001];
bool flag;
//p数组只是为输出服务
//map[i][j]表示为从i走到j可以再走中转站k后路径和能最小(只存中转站k)
//flag为检查有无中转站
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<i;j++)	e[i][j]=0x3fffff;
		for(int j=i+1;j<=n;j++)	e[i][j]=0x3fffff;
	}
    for(int i=1,x,y,z;i<=m;i++)		scanf("%d%d%d",&x,&y,&z),e[x][y]=e[y][x]=z;
	for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
        	if(i!=k)
	            for(int j=1;j<=n;j++)
	                if(j!=i && j!=k)
						if(e[i][k]+e[k][j]<e[i][j])			map[i][j]=k,e[i][j]=e[i][k]+e[k][j];
						else if(e[i][k]+e[k][j]==e[i][j])	map[i][j]=-1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if(e[i][j]!=0x3fffff && i!=j)
				if(map[i][j]!=-1)
					p[map[i][j]]=1;
	for(int i=1;i<=n;i++)
		if(p[i]==1)
			printf("%d ",i),flag=true;
	if(flag==false)											printf("No important cities.");
    return 0;
}

 

---

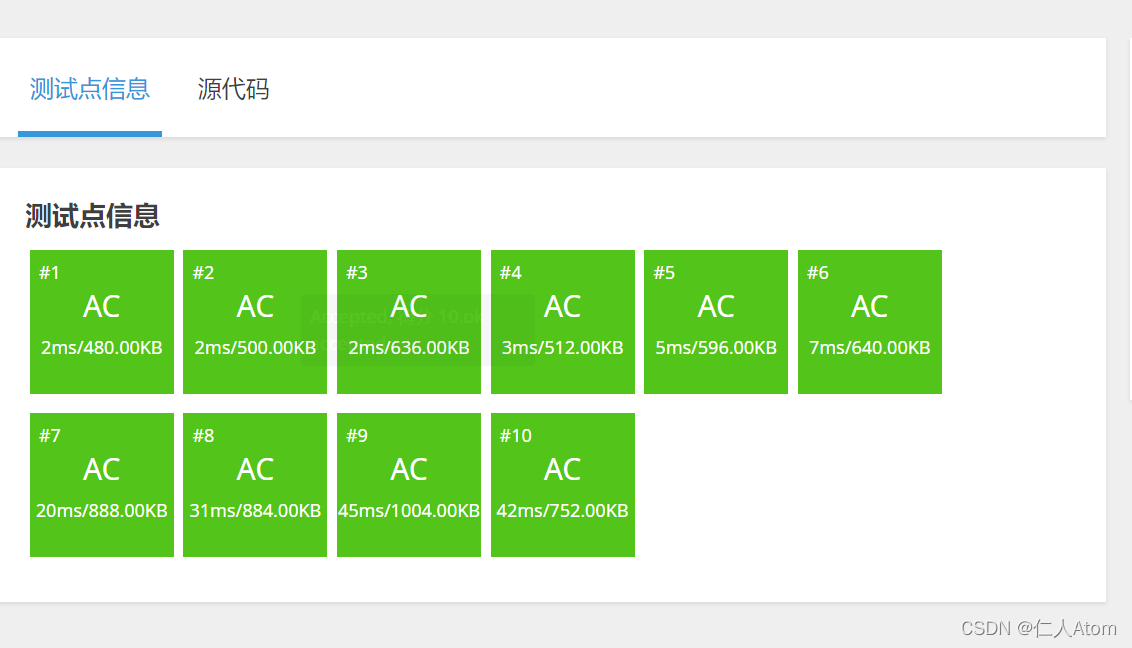
The end