03-树3 Tree Traversals Again

最新推荐文章于 2022-07-26 19:12:27 发布

大鲨鱼冲鸭

最新推荐文章于 2022-07-26 19:12:27 发布

阅读量394

点赞数 1

分类专栏： PTA 文章标签： PTA

本文链接：https://blog.youkuaiyun.com/Invokar/article/details/79979036

版权

PTA 专栏收录该内容

20 篇文章

订阅专栏

本文介绍了一种通过栈操作实现二叉树中序非递归遍历的方法，并利用给定的栈操作序列生成唯一的二叉树。文章提供了一个具体的样例分析及对应的程序代码，展示了如何从栈操作中获取前序、中序遍历序列，并进一步得到后序遍历序列。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

03-树3 Tree Traversals Again（25 分）

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

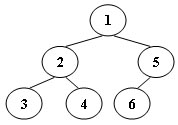
Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer $N$ ( $\leq 30$ ) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to $N$ ). Then $2 N$ lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1

解题过程：

通过Push操作，我们可以得到先序遍历的结果，通过Pop操作可以得到中续遍历的结果。这一题，可以通过不构造树，单纯用数组实现(本文参考自MOOC)。

核心算法采用的分治递归的方式。由于根节点在后续遍历中是最后访问的，先序遍历最先访问，中序遍历中间时候访问，因此可以通过根节点来分成左右两颗子树，继续调用上面的方法，即可，详细步骤在程序中已经给出注释。

可以边读程序边对本文这个例子分析，帮助理解

Pre 1 2 3 4 5 6

In 3 2 4 1 6 5

Post 3 4 2 6 5 1

程序：

#include <iostream>
#include <string>
using namespace std;

int pre[31], in[31], post[31], tempPre[31];		// 建立前序、中续、后续、存放前序遍历结果的数组

void solve(int preL, int inL, int postL, int n)        // 前序、中序、后序数组下标和结点个数
{
	if (n == 0)        // 如果没有结点，这种情况在在左右子树缺少时出现
		return;
	if (n == 1)        // 如果只剩一个结点
	{
		post[postL] = pre[preL];
		return;
	}
	int root = pre[preL], i;
	post[postL + n - 1] = root;		// 把根节点放入后续数组的尾巴上
	for (i = 0; i < n; i++)
	{
		if (in[inL + i] == root)
			break;
	}
	int L = i;			// 左分支的结点数
	int R = n - L - 1;	// 右分支的结点数，这里还要再减1是把中序遍历的根结点去掉	
	solve(preL+1, inL, postL, L);	// 递归调用左分支
	solve(preL+L+1, inL+L+1, postL+L, R); // 递归调用右分支
}

int main(int argc, char const *argv[])
{
	int N, x, idxPop = 0, idxPre = 0, tempIdxPre = 0;
	string operation;				// 表示操作
	cin >> N;
	while (idxPop < N)				// 当Pop操作达到N次说明以结束
	{
		cin >> operation;
		if (operation == "Push")
		{
			cin >> x;
			pre[idxPre++] = x;
			tempPre[tempIdxPre++] = x;
		}
		else{
			in[idxPop++] = tempPre[--tempIdxPre];	//	把tempPre数组的"栈顶"弹出放入in
		}
	}
	solve(0, 0, 0, N);
	for (int i = 0; i < N; i++)		// 输出格式
	{
		if (i != 0)
			cout << " ";
		cout << post[i];
	}
	return 0;
}

如果对您有帮助，请点个赞哦~