【WY】数据处理 — Python 阶段一：基础语法九 —— 分类分析：聚类分析

本文介绍了Python中的PCA主成分分析和K-means聚类算法。PCA作为数据降维的方法，通过线性变换降低高维数据到低维空间，而K-means是一种基于距离的聚类算法，用于将数据点分成多个簇。文章涵盖了PCA的基本理论、降维应用以及K-means的实现逻辑和注意事项。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、基础理论

1.1 聚类分析

1.1.1 介绍

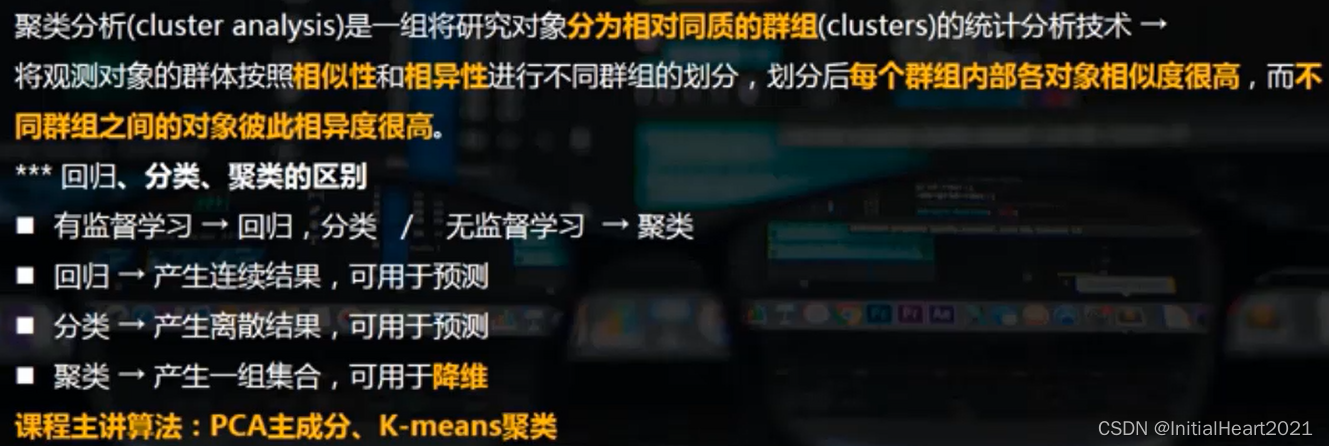
在这里插入图片描述

1.1.2 分类

1.2 矩阵分解

1.2.1 分类

1.2.1.1 PCA主成分分析

1.2.1.1.1 介绍

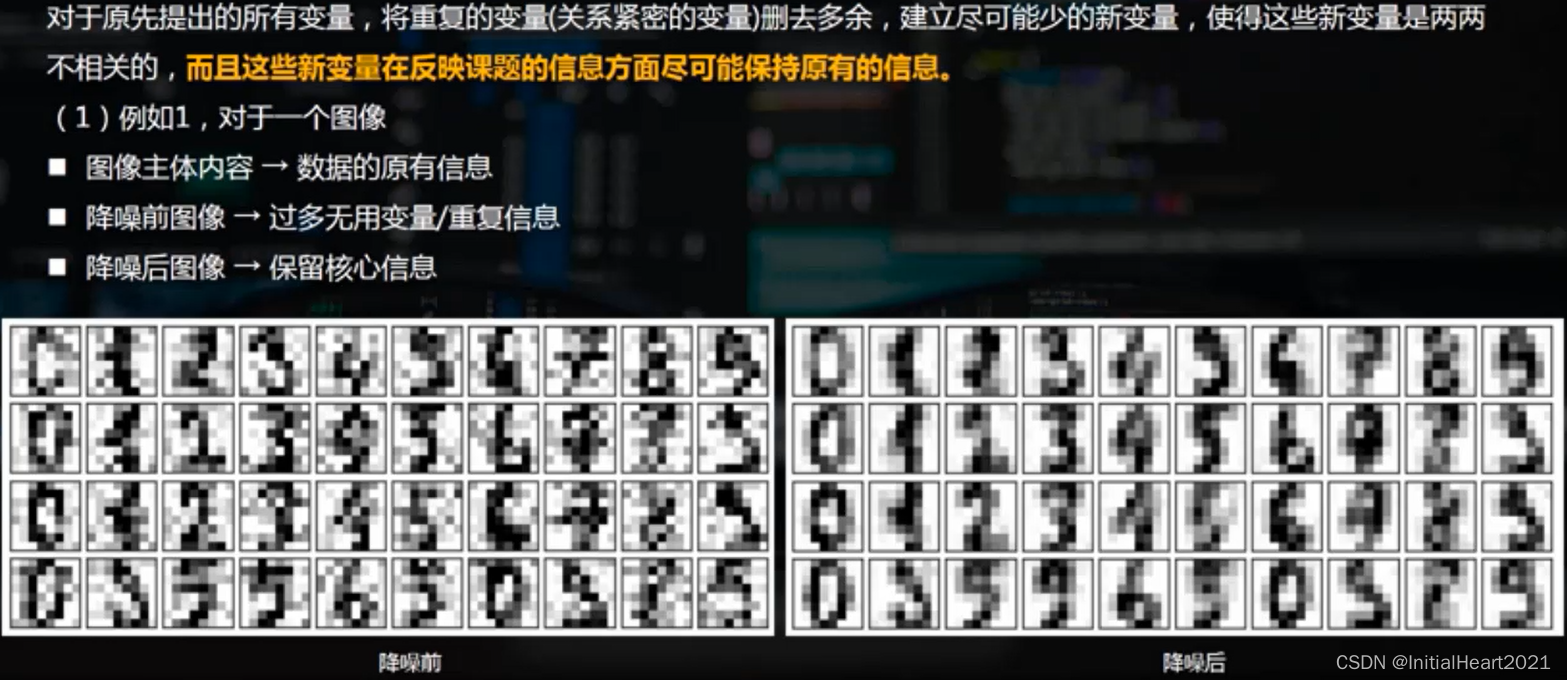
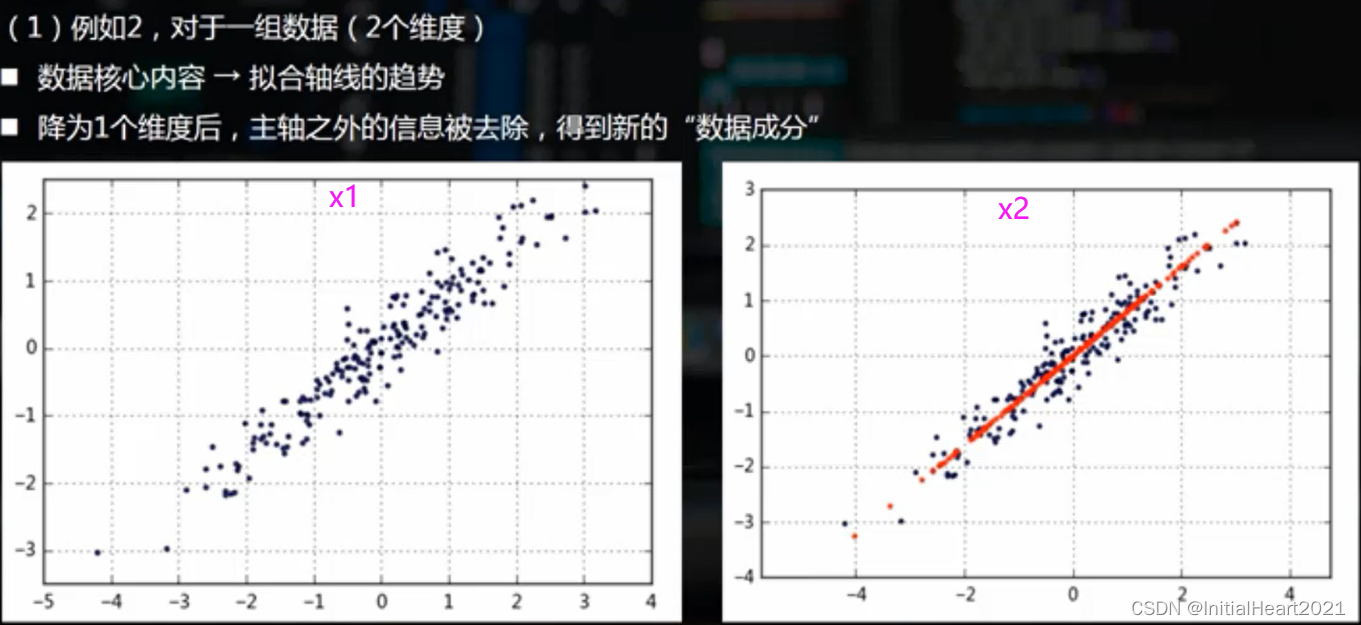
在这里插入图片描述

1.2.1.1.2 目的

在这里插入图片描述

1.2.1.1.3 降维

在这里插入图片描述

1.2.1.1.4 主成分的筛选

降维
主成分
累计贡献率

在这里插入图片描述

1.2.1.1.4 主成分的含义及用法

在这里插入图片描述

1.3 K-means聚类

在这里插入图片描述

1.3.1 K均值算法实现逻辑

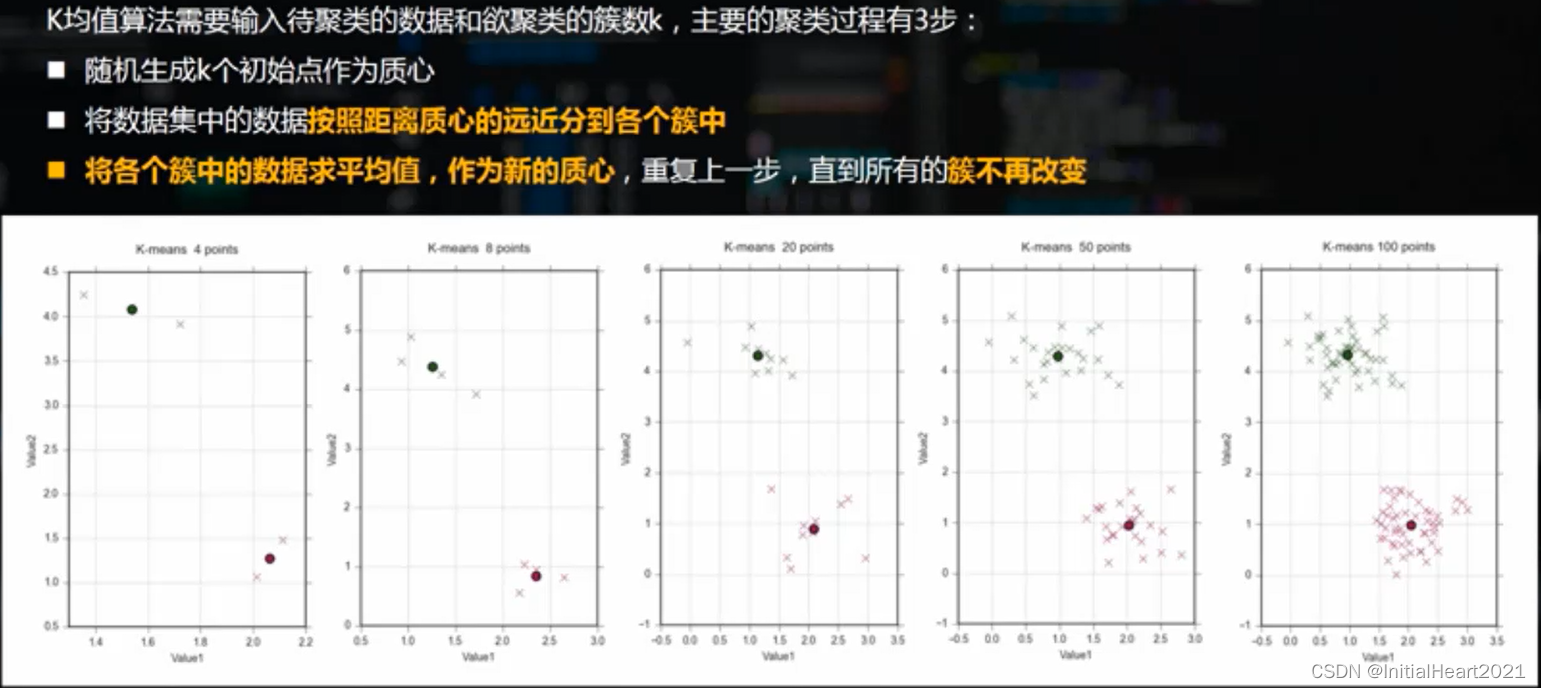
在这里插入图片描述

1.3.2 K均值聚类的注意事项

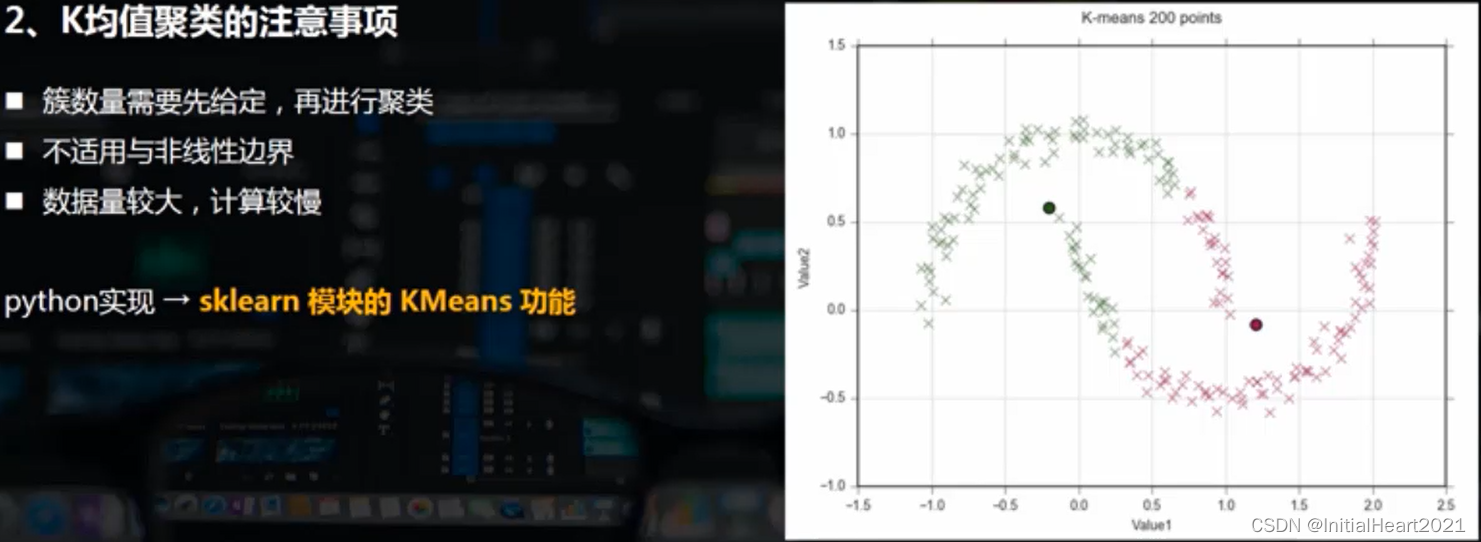
在这里插入图片描述

二、代码实现

2.1 PCA主成分分析

最广泛无监督算法 + 基础的降维算法
PCA（Principal Component Analysis）是一种常用的数据分析方法。PCA通过线性变换将原始数据变换为一组各维度线性无关的表示，可用于提取数据的主要特征分量，常用于高维数据的降维。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

# 步骤一（替换sans-serif字体）
plt.rcParams['font.sans-serif'] = ['SimHei']

# 步骤二（解决坐标轴负数的负号显示问题
plt.rcParams['axes.unicode_minus'] = False

2.1.1 二维数据降维

# 创建数据

rng = np.random.RandomState(2)

# 矩阵相乘
data = np.dot(rng.rand(2,2), rng.randn(2, 200)).T
df = pd.DataFrame({
    'X1': data[:, 0],
    'X2': data[:, 1]
})

# 散点图
plt.scatter(df['X1'], df['X2'], alpha = 0.8, marker = '.')

# 坐标轴每个单位表示的刻度相同
plt.axis('equal')
plt.grid()

2.1.1.1 2 维 ——> 1 维

sklearn.decomposition.PCA( 
	n_components=None, 
	copy=True, 
	whiten=False, 
	svd_solver='auto', 
	tol=0.0, 
	iterated_power='auto', 
	random_state=None, 
)

n_components：PCA 算法中所要保留的主成分个数 n，即保留下来的特征个数

copy：True or False，表示是否在运行算法时，将原始训练数据赋值一份

fit(X, y=None)：调用 fit方法的对象本身，如：pca.fit(X),表示用 X 对pca这个对象进行训练

# 二维数据降维：构建模型，主成分分析

# 加载主成分分析模型 PCA
from sklearn.decomposition import PCA

# 降为 1维
pca = PCA(n_components = 1)

# 构建模型
pca.fit(df)

运行结果

PCA(copy=True, iterated_power='auto', n_components=1, random_state=None,svd_solver='auto', tol=0.0, whiten=False)

# 特征值
print(pca.explained_variance_)

# 返回具有最大方差的成分，即特征向量
print(pca.components_)

# 0.68 * ((0.51 * x1) + (0.85 * x2))

运行结果

[0.67663501]

[[0.51517079 0.85708754]]

# 返回保留的成分个数
print(pca.n_components_)
print(pca.n_components)

# 结果降为几个维度，就有几个特征值；原始数据有几个维度，就有几个特征向量
print(pca.explained_variance_ratio_)

运行结果

1
1
[0.92716656]

# 这里是shape(200,2)降为shape(200,1)，只有1个特征值，对应2个特征向量
# 降维后主成分 A1 = 0.52 * X1 + 0.86 * X2
# 成分的结果值 = 0.68 * （-0.77*x1 -0.62 * x2） #通过这个来筛选它的主成分


# 数据转换，将原始二维数据转换为降维后的一维数据
df_pca = pca.transform(df)

# 数据转换，将降维后的一维数据转换成原始的二维数据
df_inverse = pca.inverse_transform(df_pca)

print('original shape：', df.shape)
print('transformed shape：', df_pca.shape)

运行结果

original shape： (200, 2)
transformed shape： (200, 1)

# 原始数据
print(df.head(10))

# 降维数据
print(df_pca[:10])

# 反算数据
print(df_inverse[:10])

运行结果

         X1        X2
0 -0.759383 -0.607229
1 -0.395182 -0.935912
2  0.236474  0.565566
3 -0.523886 -0.364576
4 -0.488779 -1.043553
5 -0.399136 -0.546887
6  0.192457 -0.502409
7  1.007959  1.403810
8  0.009926 -0.114596
9 -0.522410 -1.202168
————————————————————————————————————————————————
[[-0.9337832 ]
 [-1.02786737]
 [ 0.58444096]
 [-0.60448782]
 [-1.16834379]
 [-0.69647639]
 [-0.35358286]
 [ 1.70033598]
 [-0.11522776]
 [-1.3216165 ]]
 ————————————————————————————————————————————————
[[-0.47335483 -0.77915224]
 [-0.52182425 -0.85979061]
 [ 0.30878991  0.52209877]
 [-0.30371147 -0.49691727]
 [-0.5941936  -0.98019121]
 [-0.3511013  -0.57575954]
 [-0.17445257 -0.28186976]
 [ 0.88366643  1.47851849]
 [-0.05165898 -0.07757857]
 [-0.67315522 -1.11155934]]

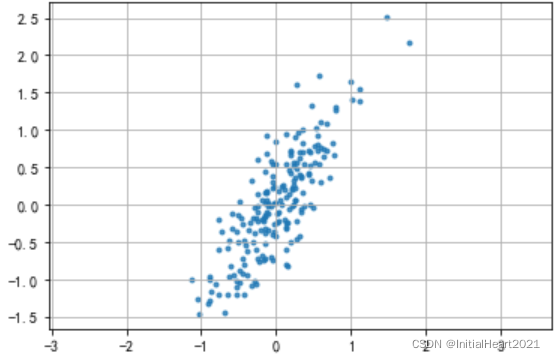
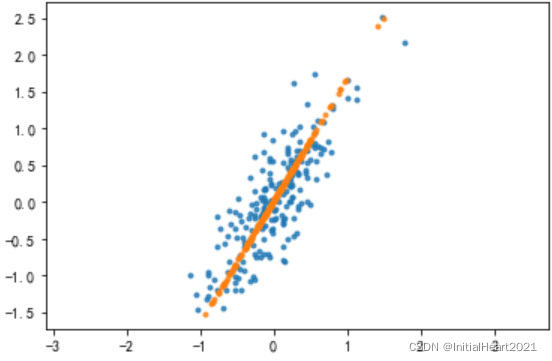
# 原始数据散点图
plt.scatter(df['X1'], df['X2'], alpha = 0.8, marker = '.')

# 转换之后的散点，红色的就是最后的特征数据
plt.scatter(df_inverse[:, 0], df_inverse[:, 1], alpha = 0.8, marker = '.')

plt.axis('equal')

2.1.2 多维数据降维

# 多维数据降维，使用自带的图像数据进行测试

from sklearn.datasets import load_digits

digits = load_digits()

print(type(digits))
print(digits.data[: 2])

# 总共1797条数据
print('数据长度为：%i 条' % len(digits['data']))

# 每条数据有 64 个变量
print('数据形状为：', digits['data'].shape)

print('字段：', digits.keys())

print('分类（数值）：', digits.target)

print('分类（名称）：', digits.target_names)

运行结果

<class 'sklearn.utils.Bunch'>

[[ 0.  0.  5. 13.  9.  1.  0.  0.  0.  0. 13. 15. 10. 15.  5.  0.  0.  3.
  15.  2.  0. 11.  8.  0.  0.  4. 12.  0.  0.  8.  8.  0.  0.  5.  8.  0.
   0.  9.  8.  0.  0.  4. 11.  0.  1. 12.  7.  0.  0.  2. 14.  5. 10. 12.
   0.  0.  0.  0.  6. 13. 10.  0.  0.  0.]
 [ 0.  0.  0. 12. 13.  5.  0.  0.  0.  0.  0. 11. 16.  9.  0.  0.  0.  0.
   3. 15. 16.  6.  0.  0.  0.  7. 15. 16. 16.  2.  0.  0.  0.  0.  1. 16.
  16.  3.  0.  0.  0.  0.  1. 16. 16.  6.  0.  0.  0.  0.  1. 16. 16.  6.
   0.  0.  0.  0.  0. 11. 16. 10.  0.  0.]]

数据长度为：1797 条

数据形状为： (1797, 64)

字段： dict_keys(['data', 'target', 'target_names', 'images', 'DESCR'])

分类（数值）： [0 1 2 ... 8 9 8]

分类（名称）： [0 1 2 3 4 5 6 7 8 9]

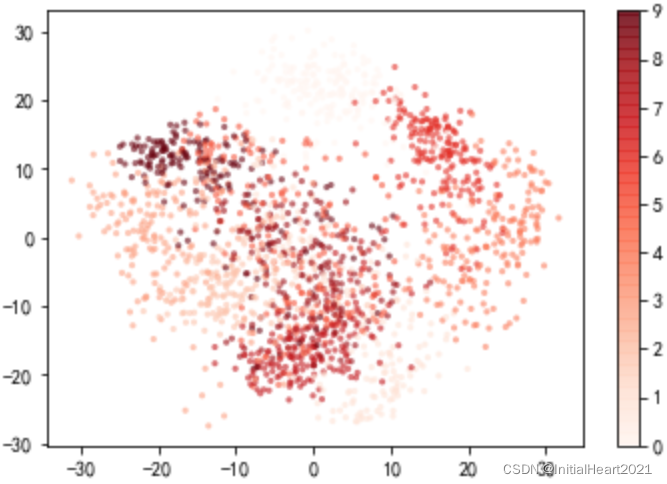
2.1.2.1 64维 ——> 2维

# 将上述数据由 64 维降为 2维，降维后的 2个维度肯定都是主成分

# 降为 2 维
pca = PCA(n_components = 2)

# 相当于先 fit 构建模型，再 transform 进行转换
projected = pca.fit_transform(digits['data'])

print('original shape：', digits['data'].shape)

print('transformed shape：', projected.shape)

# 2个 特征值
print('特征值：', pca.explained_variance_)

# 2个成分，每个成分都有64个特征向量
print('特征向量：', pca.components_.shape)

运行结果

original shape： (1797, 64)

transformed shape： (1797, 2)

特征值： [179.0069301  163.71774688]

特征向量： (2, 64)

plt.scatter(
    projected[:, 0], 
    projected[:, 1], 
    s = 10,
    c = digits.target,
    cmap = 'Reds',
    edgecolor = 'none',
    alpha = 0.6
)
plt.colorbar()

2.1.2.2 64维 ——> 10维

# 将上述数据降为10维，并求主要成分

from sklearn.datasets import load_digits

digits = load_digits()


# 降为10维
pca = PCA(n_components= 10)

# 相当于先 fit 构建模型，再 transform 进行转换
projecteds = pca.fit_transform(digits['data'])

print('original shape：', digits['data'].shape)

print('transformed shape：', projecteds.shape)

# 输出特征值 ；10个特征值
print(pca.explained_variance_)

# 输出特征向量形状
print(pca.components_.shape)

s = pca.explained_variance_

c_s = pd.DataFrame({
    'x': s,
    'x_cumsum': s.cumsum()/s.sum()
})

print(c_s)

c_s['x_cumsum'].plot(style = '--ko', linestyle = '--', figsize = (10,4))
plt.axhline(0.85, color= 'r', linestyle = '--',alpha = 0.8)
plt.text(6, c_s['x_cumsum'].iloc[6]-0.1, '第7个成分累计贡献率超过85%', color = 'r')
plt.grid()

运行结果

original shape： (1797, 64)
transformed shape： (1797, 10)
[179.0069301  163.71774688 141.78843907 101.10037264  69.51316432
  59.10849447  51.88383863  44.01507618  40.30814729  37.01123765]
(10, 64)
            x  x_cumsum
0  179.006930  0.201709
1  163.717747  0.386189
2  141.788439  0.545959
3  101.100373  0.659881
4   69.513164  0.738210
5   59.108494  0.804814
6   51.883839  0.863278
7   44.015076  0.912875
8   40.308147  0.958295
9   37.011238  1.000000

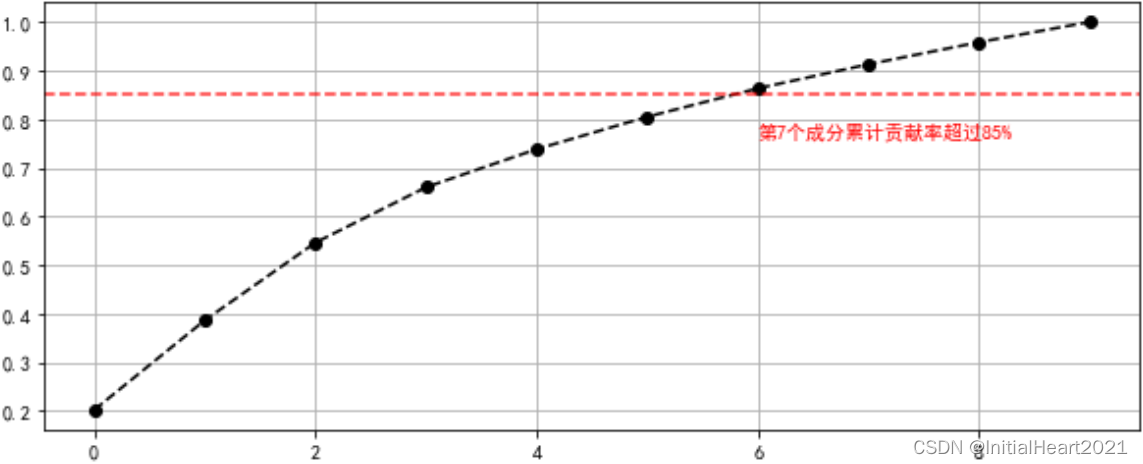
在这里插入图片描述

2.1.3 K-means聚类

K-means聚类是最常用的机器学习聚类算法，且为典型的基于距离的聚类算法。主要步骤为：

# 创建模型
kmeans = KMeans(n_clusters=4) 

# 导入数据
kmeans.fit(x) 

# 预测每个数据属于哪个类
y_kmeans = kmeans.predict(x) 

# 每个类的中心点
centroids = kmeans.cluster_centers_

1.先使用 sklearn 自带的生成器生成数据

make_blobs(
    n_samples=100,
    n_features=2,
    centers=3,
    cluster_std=1.0,
    center_box=(-10.0, 10.0),
    shuffle=True,
    random_state=None,
)

n_samples：生成的样本总数
centers：类别数
cluster_std：每个类别的方差，如果多类数据不同方差可设置为[std1,std2,...stdn]
random_state：随机数种子
x 生成的数据
y 数据对应的类别
n_features：每个样本的特征数

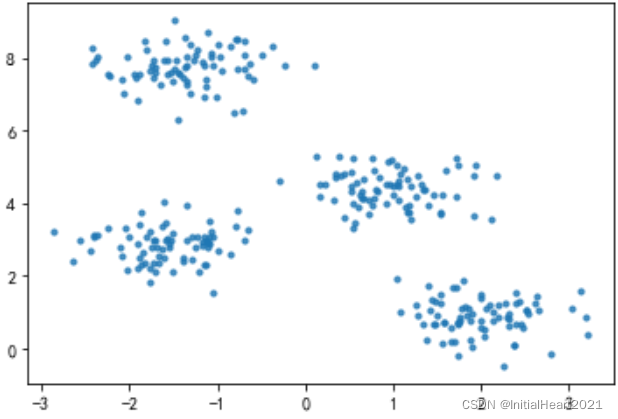
# make_blobs聚类数据生成器
from sklearn.datasets.samples_generator import make_blobs

x, y_true = make_blobs(
	n_samples=300,     # 生成300条数据
	centers=4,         # 四类数据
	cluster_std=0.5,   # 方差一致
	random_state = 0
)

plt.scatter(x[:, 0], x[:, 1], s = 10, alpha = 0.8)

# 通过sklearn的 KMeans 进行聚类分析

from sklearn.cluster import KMeans

# 创建模型
kmeans = KMeans(n_clusters=4)

# 导入数据
kmeans.fit(x)

# 预测每个数据属于哪个类
y_kmeans = kmeans.predict(x)

# 每个类的中心点
centroids = kmeans.cluster_centers_

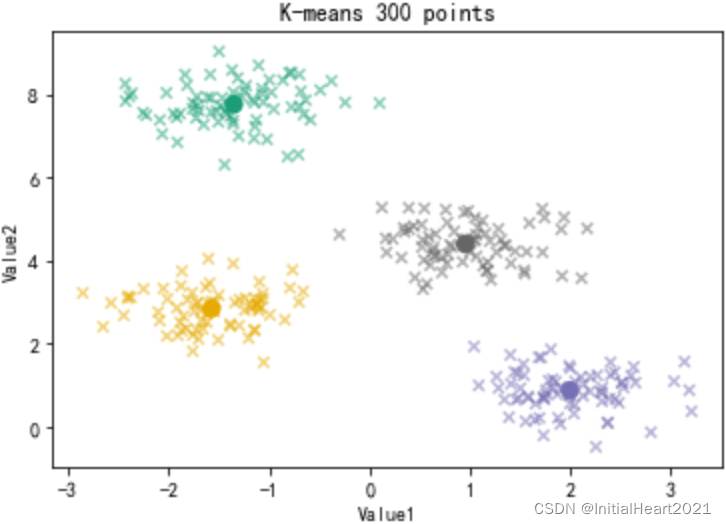
plt.scatter(x[:, 0], x[:, 1], s = 30, c = y_kmeans, cmap='Dark2', alpha = 0.5, marker='x')

plt.scatter(centroids[:, 0], centroids[:, 1], s = 70, c = [0,1,2,3], cmap = 'Dark2', marker = 'o')

plt.title('K-means 300 points')

plt.xlabel('Value1')

plt.ylabel('Value2')