蒙特卡洛树 2017 EC-Final L.SOS

蒙特卡洛树 2017 EC-Final L.SOS

最近看AlphaZero论文学习了蒙特卡洛树，隐约记得很久以前EC-Final上有人说可以利用MTC打表，决定练练手。从构建到完成耗时两天。

蒙特卡洛树的学习可以参考：https://blog.youkuaiyun.com/ljyt2/article/details/78332802

题目可以参考： https://vjudge.net/problem/1500546/origin

蒙特卡洛树主要分为tree_travelsal， node_expand,  rollout，backpropogation 四个步骤. 在本例中分别对应choose，expand， rollout， update四个函数or代码段， rollout调用wander函数来随机选取局面。

Choose Node

引入UCB函数来评判

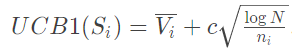
当UCB函数只根据平均值来选择node的时候很容易陷入局部最优导致局面趋于平局，这是由于每一步只有少量的选择能到达必胜态，随机漫步难以发现这种必胜态，故需要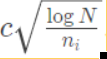使得树发现更多的新节点。

UCB函数中UCB_C值越大，越注重探索， UCB_C值越小越注重原来的选择。而C值大就意味着需要更多的迭代才能期望结果更接近最优。C值小就更可能陷入局部最优。这与过拟合非常相似。

 

PS：不同于普通的DP算法和枚举算法，蒙特卡洛树的优点是可以控制迭代次数或者迭代时间，可以以此来获得当前的最优解。

代码不足之处：MCT没有函数来清空节点内存， ans（）对最优节点的选取应该不利用UCB附加值（可以对其重写），也许可以参照AlphaZero对MCT的变体来加速

 

代码如下：

/*
author: InFiNiTeemo
substract: This program is used for solving 2017 EC-Final Problem L with low effciency for subtle computer 
to table. many program segments can be optimized as well. It's a tutoral for greenhand to understand MTC 
*/

#include<bits/stdc++.h>
#include<random>
#include<windows.h>
using namespace std;

mt19937 generator((unsigned)time(NULL));
//#define DEBUG
int sum = 0;

class Node {
private:
	const int INF = 1e8;
	const int choose[2] = { 'S', 'O' };
	const int UCT_C = 4;
	//evaluation
	double q, avg_q;
	int c;
	//transformation
	vector<Node*> son;
	//state
	vector<int> G;
	int size;
	Node* father;
	int turn; // turn & 1 enlarge the value, else ensmall the value
	bool leaf;
	int end = -2; //-2 unjudged, -1 lose, 0 don't know/ draw, 1 win
public:
	Node(int sz) :q(INF), c(0), size(sz), G(vector<int>(sz,0)), leaf(true), turn(0){}
	Node(vector<int> previous,int f_turn, int place, int kind) : c(0), size(previous.size()),G(previous), turn(f_turn+1), leaf(true){
		G[place] = kind;
		avg_q = turn & 1 ? INF : -INF;
	}
	void update(double value) {
		q += value;
		c++;
		avg_q = q / c;
	}
	double UCT() {
		if (c == 0) return avg_q;
		return avg_q + (turn&1?1:-1)* pow(UCT_C*log(sum*1.0)/c,0.5);
	}
	void add_edge(Node* son_nd) {
		son.emplace_back(son_nd);
	}
	bool is_leaf() {
		return leaf;
	}
	bool is_full() {
		return size - turn == 0;
	}
	//输出只可能是1和-1
	int is_end() {
		if (end!=-2) return abs(end);
		else return abs(end = evaluate());
	} 

	/*@The player on the offensive always choose the high score node, whereas the defensive choose the low score node, the score is based on the UCT()*/
	Node* choose_node() {
		try {
			if (turn - size == 0) {
				throw "Node.Choose Node: no left grid for node choosing.";
			}
		}
		catch(const char* msg){
			cerr << msg << endl;
		}
#ifdef DEBUG
		cout << "--------CHOOSE_NODE---------" << endl;
		show();
		cout << "----------------------------" << endl;
		Sleep(300);
#endif // DEBUG
		Node* t = NULL;
		for (auto candidate : son) {
#ifdef DEBUG
			cout << "---------------------" << endl;
			candidate->show();
			cout << "-----------------------" << endl;
			Sleep(300);
#endif // DEBUG

			if (t == NULL) t = candidate;
			else {
				//check
				double delta = candidate->UCT() - t->UCT();
				int _turn = (turn & 1 ? -1 : 1);
				if (_turn*delta > 0) {
					t = candidate;
				}
			}
		}
		return t;
	}

	Node* wander() {
		try {
			if (turn - size == 0) {
				throw "Node.Wander Node: no left grid for wandering.";
			}
		}
		catch (const char* msg) {
			cerr << msg << endl;
		}
		int left = size - turn;
		int nxt = generator()%left+1, kind = generator()%2;
		for (int i = 0; i < size; i++) {
			if (G[i] == 0) {
				nxt--;
			}
			if (nxt == 0) return new Node(G, turn, i, choose[kind]);
		}
	}
	void expand_node() {
		try {
			if (turn - size == 0) {
				throw "Node.Expand_Node: no left grid for node expanding.";
			}
		}
		catch (const char* msg) {
			cerr << msg << endl;
		}
		leaf = false;
		for (int i = 0; i < size; i++) {
			if (G[i] == 0) {
				for (int j = 0; j < 2; j++) {
					Node* son = new Node(G, turn, i, choose[j]);
#ifdef DEBUG
					cout << "-------EXPAND------------" << endl;
					son->show();
					cout << "-----------------------------" << endl;
					Sleep(300);	
#endif

					add_edge(son);
				}
			}
		}
	}
	int visit_count() {
		return c;
	}
	int evaluate() {
		for (int i = 0; i < size - 2; i++) if (G[i] == 'S'&&G[i + 1] == 'O'&&G[i + 2] == 'S') {
			return (turn & 1 ? 1 : -1);
		}
		return 0;
	}
	void show() {
		cout << "Turn: " << turn << endl;
		for (auto x : G) {
			if (x == 0) x = '-';
			cout << setw(4) << char(x);
		}
		cout << endl;
		cout << "value:  " <<UCT() << endl;
	}
};





class MTC_TREE {
private:
	Node* root;
	//size of chessboard size
	int size;
	const int iter = 1e7;

	//debug
	queue<Node*> Rollout_que;

public:
	MTC_TREE(int sz=0):size(sz) {
		root = new Node(sz);
		root->expand_node();
	}

	void game() {
		//loop
		sum = 0;
		for (int i = 0; i < iter; i++) {
			single_game();
			sum++;
		}
		//ans
		ans();
	}
	void single_game(){
		//init

		//choose
		Node* p = root;
		queue<Node*> que;
		while (!p->is_leaf()) {
			p = p->choose_node();
			Node* q = p;
			que.push(q);
		}
		//rollout
		Node* q = roll_out(p);
		//q->show();
		int x = q->evaluate();
		while(!Rollout_que.empty()) {
			Node* t = Rollout_que.front(); Rollout_que.pop();
			delete t;
		}
		//update
		while (!que.empty()) {
			Node* t = que.front(); que.pop();
			if (t->visit_count() == 0 && t->is_leaf() && !t->is_full()) {
				t->expand_node();
			}
			t->update(x);
		}
	}
	Node* roll_out(Node* p) {
		while (!(p->is_full() || p->is_end())) {
			p = p->wander();
			Rollout_que.push(p);
		}
		return p;
	}
	void ans() {
		Node* p = root;
		while (!p->is_leaf()) {
			p = p->choose_node();
		}
		//cout << (p->is_leaf()?"true":"false") << endl;
		p->show();
		string result[] = { "B win", "Draw", "A win" };
		cout << result[p->evaluate()+1] << endl;	
	}
};

int main() {
	for (int i = 3; i <= 100; i++) {
		MTC_TREE tree(i);
		cout << i << ":  ";
		tree.game();
	}
	system("pause");
}