C语言学习（8）-- 函数（2）

2. 函数递归

什么是递归？

• 函数自己调用自己就叫递归。
• 通常是把一个大型复杂的问题转化成与原问题相似的规模较小的问题
• 主要思考方式：把大事化小。

#include<stdio.h>
int main()
{
    //函数递归
    printf("hehe\n");
    main();
    return 0;
}

这就是个简单的递归例子，但是我们能发现在运行的过程中，hehe理论上来说是要持续打印的，但是实际上是会突然停止，并且会提示栈溢出的ERRO（stack overflow），这是使用递归很常见的错误。

栈溢出：在我们每次函数调用的时候都会对内存申请空间，一直到内存空间被申请完，就会出现栈溢出的现象。如下图所示。

• 有一个网站就叫做stackoverflow，相当于是程序员的知乎，知名程度类似于github
• Stack Overflow - Where Developers Learn, Share, & Build Careershttps://stackoverflow.com/

练习1：接受一个整型值（无符号）按照顺序打印它的每一位。例如：输入：1234，输出：1 2 3 4

分析：要是把一个整型值拆开打印，第一可以想到的方法就是利用%和/运算符。可是这个顺序要如何确定呢？初步想法是可以把分开的值都各自存放在一个空间，然后倒着输出即可。这个方法可行但是比较麻烦。需要利用第二种递归的方法来进行优化改进。想要实现的1234，可以按照这样的顺序进行输出。于是有了如下的程序编码。具体分析，可以看下图。

• 1234
• (123) 4
• (12) 3 4 
• (1) 2 3 4 

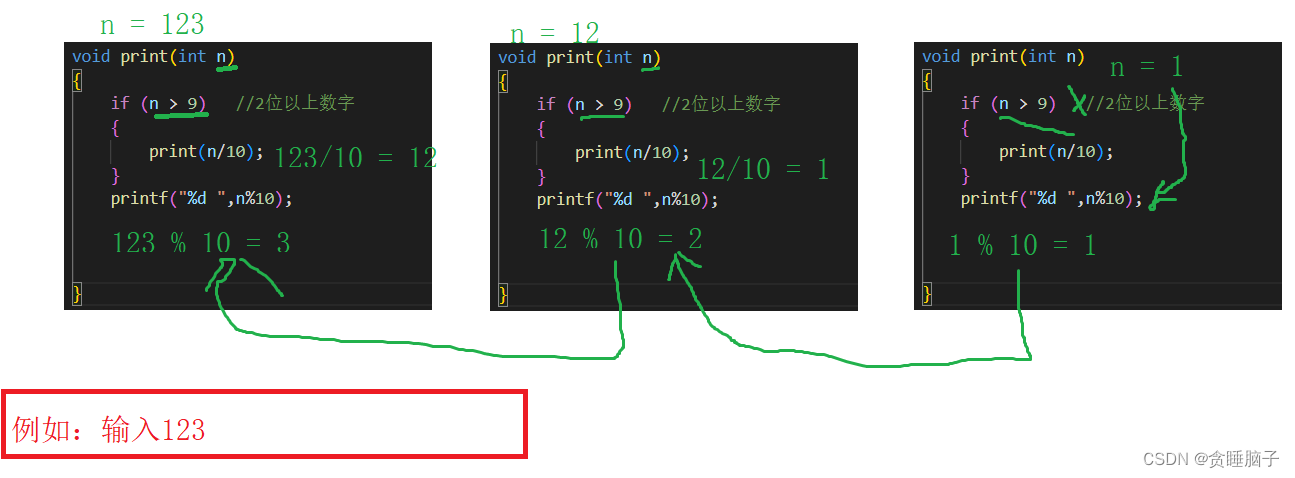
递归的两个必要条件：

• 必须要找到一个限制条件，使得递归可以停下来
• 每次递归调用之后要越来越逼近于这个限制条件。

练习2：①编写函数求字符串长度。②不创建临时变量，编写函数求字符串长度

①分析：我们知道如果求字符串的长度可以直接用strlen()的库函数实现，但是如果要自己编写一个函数就需要好好思考一下原理。字符串是以\0作为结尾的，所以我们需要找到字符不为\0的字符，并进行计数。还需要注意的是数组传参传的是首元素的地址，所以在自定义函数中的形式参数类型就应该是指针类型。

int my_strlen(char* str)
{
    int count = 0;
    while(*str != '\0')
    {
        count ++;
        str ++;
    }
    return count;
}

②分析：不让创建临时变量，就采用递归的方式。实现方式类似于练习1

• my_strleng("bit");
• 1 + my_strleng("it");
• 1 + 1 + my_strleng("t");
• 1 + 1 + 1 + my_strleng("");
• 1 + 1 + 1 + 0;
• 3

//递归方法
int my_strleng(char* str)
{
    if (*str != '\0')
    {
        return 1 + my_strleng(str + 1);
    }else
    {
        return 0;
    }
    
}

递归与迭代

练习3：求n的阶乘

int factoria(int n)
{
    if (n <= 1)
    {
        return 1;
    }
    else
    {
        return n * factoria(n-1);
    }
    
}

练习4：求第n个斐波那契数

分析：斐波那契数：1 1 2 3 5 8 13 21 34 55 ......就是前两个数字之和等于第三个数。要描述第n个斐波那契数时，前两个是1。

int fib(int n)
{
    if (n <= 2)
        return 1;
    else 
        return fib(n-1) + fib(n-2);  
}

如果根据数学方法直接编写的话，效率低，速度慢，有大量重复的计算。所以其实是不太适合用递归方法来解决的。于是想到用迭代的方式进行计算。

//法1
int Fib1(int n)
{
    int sum = 0;
    int i = 0;
    for ( i = 2; i <= n ; i++) //3-n位 从第三个开始
    {
        sum = (n-1) + (n-2);
    }
 
    return sum + 2;
    
}

//法2
int Fib2(int n)
{
    int a = 1;
    int b = 1;
    int c = 1;

    while (n > 2)
    {
        c = a + b;
        a = b ;
        b = c;
        n--;
    }
    return c;
}

选择方式的时候需要注意：①是否能功能实现②是否高效③是否栈溢出

3. 练习

1. 汉诺塔问题

2. 青蛙跳台阶问题：青蛙一次可以跳一个台阶，一次也可以跳2个台阶，要是跳到第n个台阶，有多少种跳法？