历届试题 九宫重排

问题描述
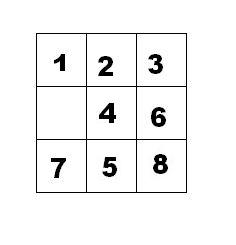
　　如下面第一个图的九宫格中，放着 1~8 的数字卡片，还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动，可以形成第二个图所示的局面。
　　
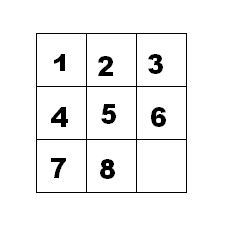
　　我们把第一个图的局面记为：12345678.
　　把第二个图的局面记为：123.46758
　　显然是按从上到下，从左到右的顺序记录数字，空格记为句点。
　　本题目的任务是已知九宫的初态和终态，求最少经过多少步的移动可以到达。如果无论多少步都无法到达，则输出-1。

输入格式
　　输入第一行包含九宫的初态，第二行包含九宫的终态。
输出格式
　　输出最少的步数，如果不存在方案，则输出-1。
样例输入
12345678.
123.46758
样例输出
3
样例输入
13524678.
46758123.
样例输出
22

思路：
emmm算法渣渣表示真的不会这题-.- 下面的思路借鉴大佬的，真的要好好学了（PS：如果不是疫情推迟，明天就GG了）

我们可以把每一种局面当作是一个结点。空白格可以向四个方向移动，移动后的局面是新的结点。显然，我们可以通过bfs来搜索目标局面，并且一旦搜索到就一定是最少移动次数。我们需要解决的问题有两个。

1：如何记录每一种局面。

2：如何判断当前局面是否已经出现过，即之前的搜索过程中已经搜索过了，简单点说就是判重。

问题1解决方法：

我们可以通过声明二维数组，int a[maxstate][9], a[1][9]表示第一种局面，a[2][9]表示第二种局面，这里我们为了表示方便，typedef int State[9]; State st[maxstate];这样的话，第i种局面就可以用st[i]表示。

问题2解决方法：

非常直接的方法声明数组vis[9][9][9][9][9][9][9][9][9]，这样的一个九维数组，显然，这样做并不是那么合理的。这里所用的方法是哈希映射。

备注：

1：memcmp();memcpy(); memset();

2：我们把3*3的九宫格的数字按照一行一行的从左往右的顺序处理成一行数据。假设在这一行数据中他的位置是n，那么他在二维表中的位置就是（n/3, n%3）。

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;

string str1,str2;
typedef int State[9];
int maxstate=1000000;
State st[1000000],goal;
int dist[1000000];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};

const int hashsize=1000003;
int head[hashsize],next[hashsize];

int hash(State &s){
	int v=0;
	for(int i=0;i<9;i++)
		v=v*10+s[i];//把9个数字组合成9位数
	return v%hashsize;//确保hash函数值是不超过hash表的大小的非负整数 
}

int try_to_insert(int s){
	int h=hash(st[s]);
	int u=head[h];//从表头开始查找链表
	while(u){
		if(memcmp(st[s],st[u],sizeof(st[s]))==0)
			return 0;//有重复，插入失败
		u=next[u];//顺着链表继续找 
	} 
	next[s]=head[h];//该结点插入到链表中
	head[h]=s;
	return 1; 
}

void init_table(){
	memset(head,0,sizeof(head));
}

int bfs(){
	init_table();//初始化查找表
	int front=1,rear=2;
	while(front<rear){
		State& s=st[front];
		if(memcmp(goal,s,sizeof(s))==0) return front;
		int z;
		for(int i=0;i<9;i++)
			if(!s[i]) z=i;//找“0”的位置
		int x=z/3,y=z%3;
		for(int i=0;i<4;i++){
			int newx=x+dx[i];
			int newy=y+dy[i];
			int newz=newx*3+newy;
			if(newx>=0 && newx<3 && newy>=0 && newy<3){
				State& t=st[rear];
				memcpy(&t,&s,sizeof(s));//扩展新节点
				t[newz]=s[z];
				t[z]=s[newz];
				dist[rear]=dist[front]+1;
				
				if(try_to_insert(rear)) rear++;//查重，修改队尾指针 
			}
			 
		} 
		front++;
	}
	return 0; 
}

int main(){
	cin>>str1>>str2;
	for(int i=0;i<9;i++){
		if(str1[i]=='.')
			st[1][i]=0;
		else
			st[1][i]=str1[i]-'0';
	}
	for(int i=0;i<9;i++){
		if(str2[i]=='.')
			goal[i]=0;
		else
			goal[i]=str2[i]-'0';
	}
	int ans=bfs();
	if(ans==0)
		printf("%d\n",-1);
	else
		printf("%d\n",dist[ans]);
	return 0;
}

原文链接：https://blog.youkuaiyun.com/qq_34594236/article/details/64446491