《剑指offer》【面试题八：旋转数组的最小数字】

面试题八：旋转数组的最小数字

算法的考察也是面试的一大重点，所以对于二分查找、归并查找、快速排序这几个经常考的，也是要记得滚瓜烂熟。

在写代码的时候，有很多算法都会用到循环和递归这两种不同的方法实现，通常递归的实现方式是比较简单，代码比较简洁，但是它的缺点就是在效率方面不如用循环来实现代码。所以在面试官没有具体的要求的时候，我们可以用递归，但是如果对代码的整体的效率方面进行考虑的话，尽量不要使用递归。

面试题八：旋转数组的最小数字；

题目：

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增

排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个 旋转,该数组的最小值为1。

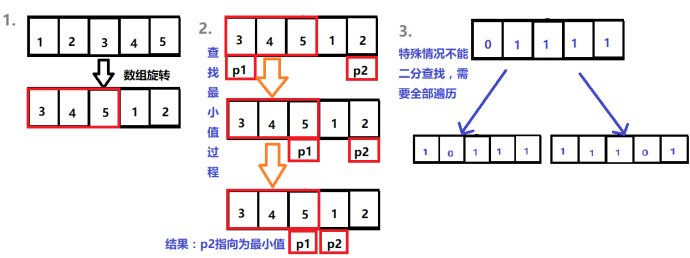
分析：第一种就是从尾到头遍历整个数组，时间复杂度为O(n)也是直接可以想到的一种方法，但是题目中给出你旋转数组的定义，就不可能直接让你去想到解决掉，毕竟面试也是对人才的一种筛选。所以我们从另一种角度去思考问题，一开始是有序的一个数组，那么经过旋转，我们就会发现原本的一个数组相当于拆成了两个有序的数组，但是原本的特性有序并没有发生改变，我们这里说的特性没有改变是指旋转后的"两个数组"，所以我们可以找到两个数组的交接点，就是临界点，不难发现是1，那么我们怎么从一个数组的角度去思考两个数组的问题呢，首先，一个数组从前想后是下标进行移动，那么使一个数组可以想象成两个数组，所以我们就使用两个“下标”，也就是两个"指针",p1和p2，p1从下标0（第一个元素）开始，p2从尾部（最后一个元素）开始，并且由于是“旋转”得到，所以一般情况左边的数组会大于等于右边的数组，这样我们就可以利用二分查找的特性进行解决了，接着我们找到数组中的中间元素，使p1下标所对应的元素与中间元素进行比较，如果中间元素大于p1，说明在“左边数组中”，所以，我们直接把p1跳到中间元素的位置上，同样的当中间元素与p2进行比较的时候，由于p2是从后向前与原数组的有序相反，所以利用这特效，当中间元素小于p2的时候说明，中间元素在“右边的数组”中，所以p2跳到中间元素的位置上。所以这样，一步一步的就会使范围不断缩小，也就是所谓的二分查找算法原理。

所以时间复杂度为O(logn),特殊情况为O(n)，比如数组为{0,1，1,1,1}旋转得到数组{1,0,1,1,1}和{1,1,1,0,1}；这时候我们计算就会发现p1所对的和p2还有中间元素相等，所以就会使两个指针p1和p2不知道怎么移动，所以对于这种特殊情况只能顺序查找了，也就是时间复杂度为O(n)。

图解：

代码实现：

#include <iostream>
#include <assert.h>
using namespace std;

int find_min_number(int *num, int len)
{
	assert(num != NULL && len > 0);

	int index_left = 0;
	int index_right = len-1;
	int index_mid = index_left;

	while(num[index_left] >= num[index_right])
	{
		if (index_left+1 == index_right)
		{
			index_mid = index_right;
			break;
		}
		index_mid = (index_left+index_right) / 2;
		if (num[index_left] == num[index_right] && num[index_right] == num[index_mid])
		{
			for (int i = index_left+1; i<index_right; i++)
			{
				if (num[index_left] > num[i])
				{
					index_left = i;
				}
			}
			index_mid = index_left;
			break;
		}
		if (num[index_left] <= num[index_mid])
		{
			index_left = index_mid;
		}
		else if(num[index_right] >= num[index_mid])
		{
			index_right = index_mid;
		}
	}
	return num[index_mid];
}




int main()
{
	//测试用例：

	//输入的数组是升序排序数组的一个旋转，数组没有重复数字；
	int num1[5] = {3,4,5,1,2};
	cout<<"min_num:  "<<find_min_number(num1,sizeof(num1)/sizeof(num1[0]))<<endl;
	//输入的数组是升序排序数组的一个旋转，数组有重复数字；
	int num2[6] = {3,4,5,1,2,3};
	cout<<"min_num:  "<<find_min_number(num2,sizeof(num2)/sizeof(num2[0]))<<endl;
	//输入的数组是一个升序排序的数组；
	int num3[6] = {1,2,3,4,5,6};
	cout<<"min_num:  "<<find_min_number(num3,sizeof(num3)/sizeof(num3[0]))<<endl;
	//输入的数组只包含一个数字；
	int num4[1] = {1};
	cout<<"min_num:  "<<find_min_number(num4,sizeof(num4)/sizeof(num4[0]))<<endl;
	//特殊输入测试（NULL指针）
	int *num5 = NULL;
	cout<<"min_num:  "<<find_min_number(num5,sizeof(num5)/sizeof(num5[0]))<<endl;
	
	return 0;
}