第七章:时间序列模型
第二部分:时间序列统计模型与神经网络模型
第一节:简单序列模型: moving average, linear model and exponential smoothing介绍及代
一、引言:从简单模型理解时间序列
在复杂的时序模型(如 ARIMA、LSTM)出现之前,最早的时间序列预测方法都来自于统计建模思想。
这些模型往往不需要大规模数据或复杂网络,仅依赖于过去观测值的线性关系与加权平滑机制即可实现稳定预测。
本节我们将从三个最基础的模型入手:
移动平均(Moving Average, MA)
线性回归时序模型(Linear Model)
指数平滑模型(Exponential Smoothing)
它们构成了现代时间序列分析的基石。
二、移动平均模型(Moving Average, MA)
1. 原理介绍
移动平均是一种最简单的平滑方法。
它通过对最近一段时间的观测值取平均,消除随机波动,突出数据的趋势性。
公式如下:
其中 (k) 是滑动窗口大小,(\hat{y}_t) 为预测值。
直观理解:
-
窗口越大 → 越平滑,但响应变化越慢;
-
窗口越小 → 响应快,但更容易受噪声干扰。
2. 代码实战
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 模拟数据:带噪声的趋势序列
np.random.seed(42)
t = np.arange(100)
y = 0.5 * t + np.random.randn(100) * 5
series = pd.Series(y)
# 移动平均平滑
ma_3 = series.rolling(window=3).mean()
ma_7 = series.rolling(window=7).mean()
plt.plot(series, label='原始数据', alpha=0.6)
plt.plot(ma_3, label='3步移动平均')
plt.plot(ma_7, label='7步移动平均')
plt.legend()
plt.show()
应用:股票价格短期趋势、传感器信号降噪、Web流量平滑等。
三、线性模型(Linear Model)
1. 原理
线性模型通过拟合时间与观测值之间的线性关系实现预测。
其核心思想:
其中 表示趋势斜率,
为残差。
若考虑多特征(如节假日、温度),则可以扩展为多元线性模型。
2. 代码实战
from sklearn.linear_model import LinearRegression
# 构建时间索引
t = np.arange(len(series)).reshape(-1, 1)
model = LinearRegression()
model.fit(t, series)
# 拟合与预测
y_pred = model.predict(t)
plt.plot(series, label='原始数据', alpha=0.6)
plt.plot(y_pred, label='线性拟合趋势', color='red')
plt.legend()
plt.show()
print("趋势斜率 β1 =", model.coef_[0])
应用:长期趋势预测、经济指标分析(如GDP增长、销售量趋势)。
四、指数平滑模型(Exponential Smoothing)
1. 核心思想
指数平滑是一种改进的加权平均方法:
越近的时间点权重越高,越远的时间点权重越低。
其思想是:
其中:
-
为平滑系数;
-
越大 → 越重视最近数据。
这种方法可以递归实现预测,非常适合实时更新。
2. 单指数平滑(Simple Exponential Smoothing)
from statsmodels.tsa.holtwinters import SimpleExpSmoothing
model = SimpleExpSmoothing(series)
fit = model.fit(smoothing_level=0.2, optimized=False)
y_pred = fit.fittedvalues
plt.plot(series, label='原始数据')
plt.plot(y_pred, label='指数平滑(α=0.2)')
plt.legend()
plt.show()
3. 双指数平滑(Holt’s Linear)
考虑到趋势成分,Holt 对平滑进行了扩展: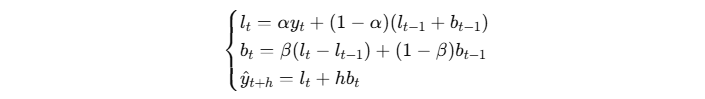
代码实现:
from statsmodels.tsa.holtwinters import ExponentialSmoothing
model = ExponentialSmoothing(series, trend='add', seasonal=None)
fit = model.fit()
fit.fittedvalues.plot(label='Holt平滑预测')
series.plot(label='原始数据')
plt.legend()
plt.show()
4. 三指数平滑(Holt-Winters)
当数据存在明显季节性时,需再加入季节分量:
可通过 seasonal='add' 或 'mul' 实现。
五、三者对比总结
| 模型 | 核心思想 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| Moving Average | 简单平均平滑 | 实现简单、稳定 | 反应慢、不适合趋势数据 | 降噪、短期平滑 |
| Linear Model | 拟合时间线性关系 | 可解释性强 | 难应对非线性趋势 | 长期趋势预测 |
| Exponential Smoothing | 权重递减的平滑 | 响应灵敏、支持趋势/季节 | 参数调优复杂 | 实时预测、季节性序列 |
六、实践建议
-
先从简单模型出发
-
若序列平稳且噪声大 → Moving Average。
-
若趋势明显 → Linear 或 Holt 模型。
-
若季节性强 → Holt-Winters 模型。
-
-
调优策略
-
α越大越重视近期变化; -
可通过验证集误差(如 RMSE)选择最优参数。
-
-
与现代模型结合
-
这些方法常作为基线模型(Baseline),
用于与 LSTM、Transformer 等复杂模型性能对比。
-
七、小结
本节我们系统地介绍了三种最基础的时间序列建模方法:
| 模型 | 关键词 | 本质 |
|---|---|---|
| Moving Average | 平滑噪声 | 窗口加权 |
| Linear Model | 趋势拟合 | 线性回归 |
| Exponential Smoothing | 加权递归 | 平滑更新 |
它们的思想虽然简单,但在实际工业预测中仍被广泛使用,尤其在低延迟、低计算开销场景下具有巨大优势。
一句话总结:
“简单的时间序列模型,是理解复杂预测算法的最佳起点。”






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








