【数据结构】——BST二叉搜索树

BST树——二叉平衡/搜索树

它的特点是：

• 左孩子的值 < 根的值；根的值 < 右孩子的值；
• 所有关键码的结点都不相同；
•  左右子树也都是二叉搜索树；
• 并且BST树不一定是一棵完全二叉树。

对这样一棵二叉搜索树，进行中序遍历，可以按从小到大的顺序将各节点关键码排列起来，所以也称二叉搜索树为二叉排序树。

1、定义二叉搜索树的结构

结点结构：

typedef int KeyType;
typedef struct BstNode
{
    BstNode* leftchild;
    BstNode* parent;
    BstNode* rightchild;
    KeyType data;
}BstNode;

二叉搜索树的每个节点都包含四个域，左右孩子域，双亲域以及对应的关键码。

树结构：

typedef struct
{
    BstNode* head;//头结点
    int cursize;//结点个数
}BSTree;

         头结点域和节点个数；

对于每一种数据结构我们都会有增删改查等这些基本功能。由于二叉搜索树的特性，在进行查找的时候，注意，它不会从左子树跳到右子树，相反也不会从右子树跳到左子树。

2、查找

查找从递归和非递归两种来进行实现。要明确的一点是在左子树或者右子树中没有找到的时候不会回到另外一部分右子树或左子树中。因为这是一颗有序树。

//非递归查找 kx 
BSTNode *FindValue(BSTree &bt,Elemtype kx)
{
	BSTNode *p = bt.head->parent;
	while(p != NULL && p->data != kx)
	{
		p = kx < p->data?p->leftchild:p->rightchild;
	}	
	return p;
}
//递归查找kx
BSTNode * Search(BSTNode *p,Elemtype kx)
{
	if(p == NULL || p->data == kx)
		return p;
	else if(kx < p->data)
		return Search(p->leftchild,kx);
	else
		return Search(p->rightchild,kx);
}
BSTNode *SearchValue(BSTree &bt,Elemtype kx)
{
	BSTNode *p = bt.head->parent;
	return Search(p,kx);
}

3、插入

//插入
bool InsertItem(BSTree &bt,Elemtype kx)
{
	BSTNode *pa = bt.head;
	BSTNode *p = bt.head->parent;
	while(p != NULL && p->data != NULL)
	{
		pa = p;
		p = kx < p->data?p->leftchild:p->rightchild;
	}
	if(p != NULL)
	{
		return false;
	}
	p = Buynode(pa);
	p->data = kx;
	if(pa == bt.head)
	{
		bt.head->parent = p;
		bt.head->leftchild = p;
		bt.head->rightchild = p;
	}
	else
	{
		if(p->data < pa->data)
		{
			pa->leftchild = p;
			if(p->data < bt.head->leftchild->data)
			{
				bt.head->leftchild= p;
			}
		}
		else
		{
			pa->rightchild = p;
			if(p->data > bt.head->rightchild->data)
			{
				bt.head->rightchild= p;
			}
		}
	}
	bt.cursize+=1;
	
	return true;
}

4、中序遍历  递归  非递归

//递归
void InOrder(BSTNode *p)
{
	if(p != NULL)
	{
		InOrder(p->leftchild);
		cout << p->data << " ";
		InOrder(p->rightchild);
	}
}
void InOrder(BSTree &bt)
{
	InOrder(bt.head->parent);
	cout << endl;
}
//非递归
void NiceInOrder(BSTree &bt)
{
	for(BSTNode *p = First(bt.head->parent);p!=NULL;p = Next(bt,p))
	{
		cout << p->data<<" ";
	}
	cout << endl;
}
int GetSize(BSTree &bt)
{
	return bt.cursize;
}
bool Empty(BSTree &bt)
{
	return GetSize(bt) == 0;
}

5、前驱和后继的查找

BSTNode *First(BSTNode *ptr)
{
	while(ptr != NULL && ptr->leftchild != NULL)
	{
		ptr = ptr->leftchild;
	}
	return ptr;
}
BSTNode *Next(BSTree &bt,BSTNode *ptr)
{
	if(ptr == NULL || ptr == bt.head)
	{
		return NULL;
	}
	if(ptr->rightchild != NULL)
	{
		return First(ptr->rightchild);
	}
	else
	{
		BSTNode *pa = ptr->parent;
		while(pa != bt.head && pa->leftchild != ptr)
		{
			ptr = pa;
			pa = pa->parent;
		}
		if(pa == bt.head)
		{
			pa = NULL;
		}
		return pa;
	}
}

6、删除元素

删叶子节点

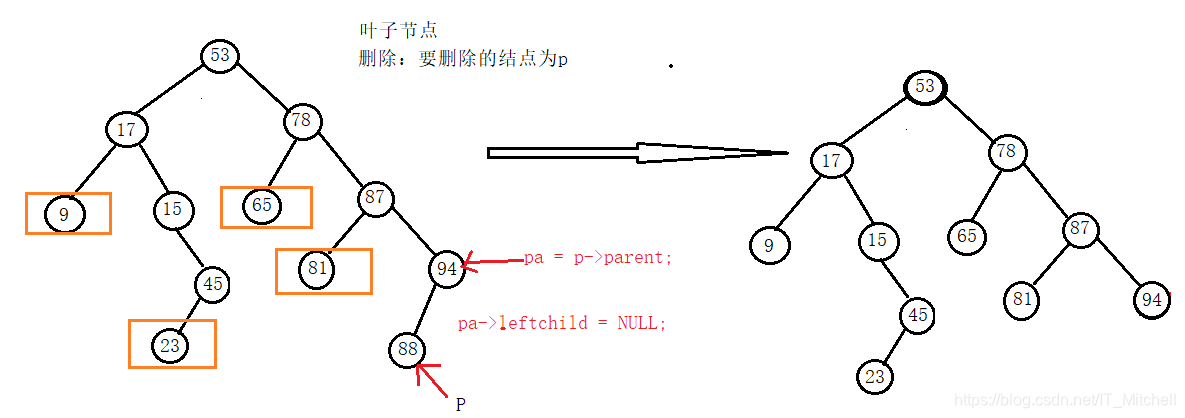
删单分支

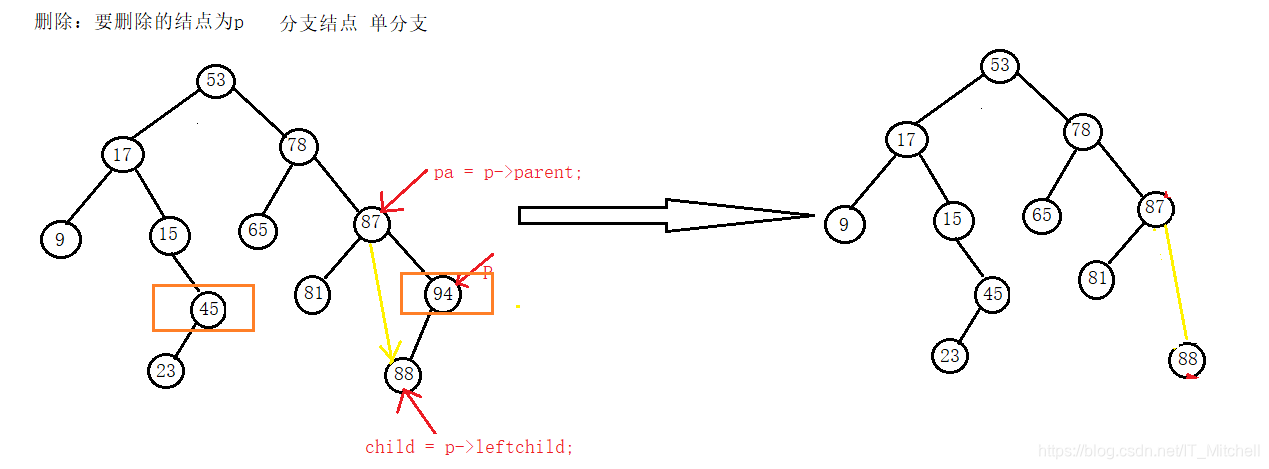
删双分支，

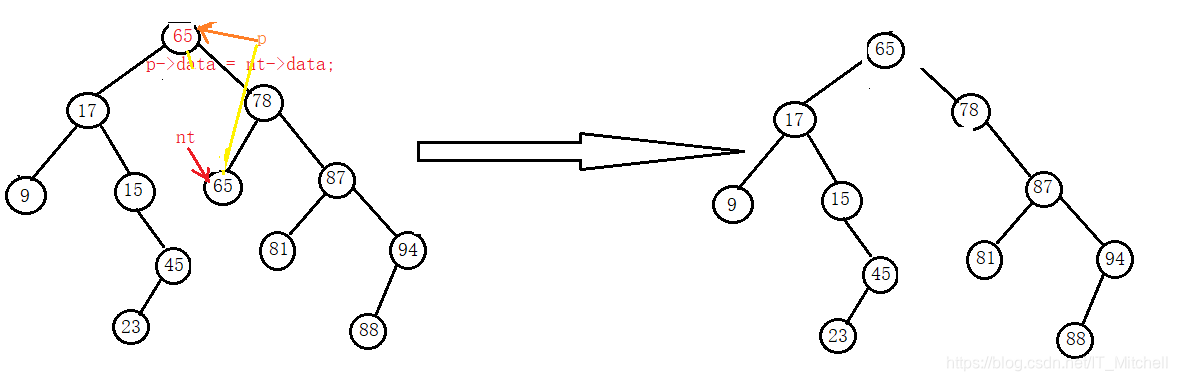
代码：

bool RemoveItem(BSTree &bt,Elemtype kx)
{
	if(Empty(bt))
		return false;
	BSTNode *p = FindValue(bt,kx);
	if(NULL == p)  return false;
	//找到了所要删除的结点
	if(p->leftchild != NULL && p->rightchild != NULL)
	{
		BSTNode *nt = Next(bt,p);
		p->data = nt->data;
		p = nt;
	}
	BSTNode *pa = p->parent;
	BSTNode *child = p->leftchild != NULL ? p->leftchild:p->rightchild;
	if(child != NULL)		child->parent =pa;
	if(pa == bt.head)		bt.head->parent = child;
	else
	{
		if(pa->leftchild == p)
		{
			pa->leftchild = child;
		}
		else
		{
			pa->rightchild = child;
		}
	}
	FreeTree(p);
	bt.cursize -= 1;
	return true;
}

 

小结：

BST树是一棵平衡二叉树也称二叉搜索树，它的主要特点就是左子树的值均小于根的值，右子树的值均大于根的值，因此中序遍历的结果是有序的并且结点的元素是不允许重复的。

在进行BST树的插入时，根据左<根，根<右这一特性进行插入，我这里构建的是带头结点的BST树，所以当head的parent域为空时，说明我们插入的是第一个结点，就将其构建在根节点上；当依次进行插入时，判断与根节点的大小关系，分别进行左子树或者右子树的向下遍历；切记，不会出现从左子树跳到右子树进行插入的情况；

删除结点时，分析是层层递进的，在BST树中，叶子节点是最容易删除的，只需要让它的双亲的左/右孩子域指向空，将结点个数减一即可；那接下来是对单分支的分析，单分支的删除也相对比较容易，它只有一个孩子左/右，删除时，只需要让其双亲的左/右指针域指向它的孩子，然后将结点个数减一；相对较难的就是我们的双分支结点，删除具有双分支的结点时，说明这个结点是根节点(不一定是整棵树的根)，我们需要将其根节点与它的后继（根据BST树的特点，根节点的后继一定一个叶子节点），将后继结点作为新根后，让原来指向根节点的p指针指向后继结点，删除后继结点，节点个数减一即可；