不同路径--动态规划

题目：

不同路径:每次只能向下或者向右移动，从左上角出发到达右下角，共有多少条不同的路径？

思想：

其实针对此问题我们可以用动态规划的思想来解决，对于第一行和第一列来说，只有一条路径，所以初始化为1

                                                                             

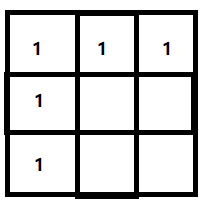
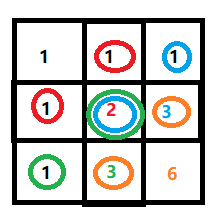
接着我们可以观察看出，到达dp[1][1]的路径主要可以和dp[1][0]和dp[0][1]有关，到达这两点后对于通向dp[1][1]是一样的，所以我们可以推导出到达当前点的路径数和它的同行前一列和前一行同列的路径数有关，即：dp[i][j] = dp[i - 1][j] + dp[i][j - 1];

                                                                             

 int uniquePaths(int m, int n) 
{
    int **dp = new int*[m];//先使一个二级指针指向数组指针的地址

	for(int i = 0 ; i < m ;++i )
	{
		dp[i] = new int[n]();//为一级指针分配地址
	}

    for (int i = 0; i < n; i++) dp[0][i] = 1;
    for (int i = 0; i < m; i++) dp[i][0] = 1;
    for (int i = 1; i < m; i++) {
        for (int j = 1; j < n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    return dp[m - 1][n - 1];  
}

 int main()
 {
	 int m,n;
	 cin >> m >> n ;
	 cout << uniquePaths(m,n) << endl;
 }

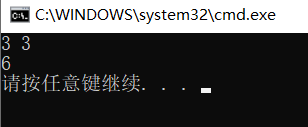
  结果如下：