113. Path Sum II

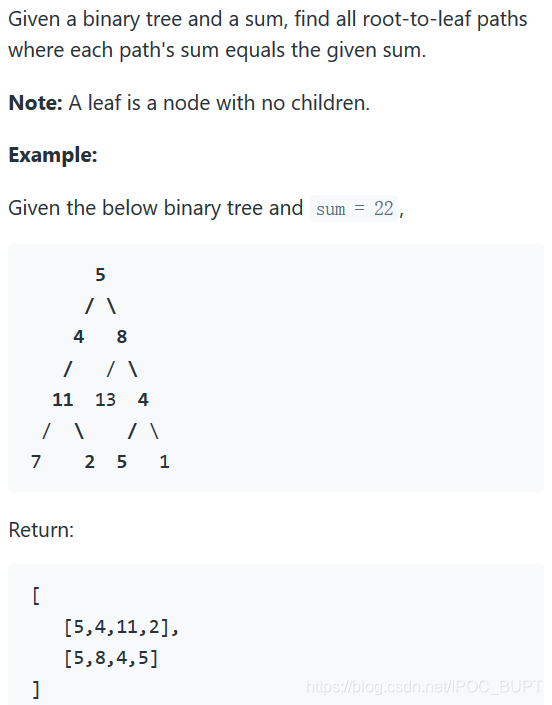
题目描述

方法思路

搜索方法为深度优先搜索，遍历顺序为先序遍历。
本题中，因为满足要求的路径并不唯一，需要用回溯的思想来解决。
简述思路如下：
1、先序遍历，从根节点开始添加，然后搜索左子树，一直达到叶子节点，得到根叶路径5-4-11–7，检验是否满足要求。
2、随后进行回溯，从队列尾部删除一个数据，返回到根结点11，然后搜索其右子树，根叶路径为5-4-11-2，检验是否满足要求。
3、如此反复。
需要注意的是，执行回溯操作的两个位置：
1、遍历至叶节点，得到一个根叶路径，如果满足约束则保存，然后回溯到根结点。
2、一根节点的左右子节点遍历结束，如节点11的左右子节点7、2便利结束，则进行回溯，当前list存储的路径为5-4.

class Solution{
    //Runtime: 1 ms, faster than 99.94%
    //Memory Usage: 39.4 MB, less than 72.24%
    List<List<Integer>> result  = new LinkedList<List<Integer>>();
    public List<List<Integer>> pathSum(TreeNode root, int sum){
	    List<Integer> currentResult  = new LinkedList<Integer>();
	    dfs(root,sum,currentResult);
	    return result;
    }

public void dfs(TreeNode root, int sum, List<Integer> currentResult) {
	if (root == null) return;
    currentResult.add(root.val);
	
	if (root.left == null && root.right == null && sum == root.val) {
		//为什么要new呢？,如果直接添加，后续的改变发生，已经添加的集合也会做同样的改变。
		result.add(new LinkedList(currentResult));
		//don't forget to remove the last integer
		currentResult.remove(currentResult.size() - 1);
		return;
	} else {
		dfs(root.left, sum - root.val, currentResult);
		dfs(root.right, sum - root.val, currentResult);
	}
    
	currentResult.remove(currentResult.size() - 1);
    }
}