算法笔记3——从凸优化问题角度看SVM

最新推荐文章于 2024-10-20 11:19:20 发布
原创 最新推荐文章于 2024-10-20 11:19:20 发布 · 1.7k 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#svm

0 常考知识点

惩罚因子C，越大，过拟合，无穷大时变为硬间隔

合页损失 max(0, 1-Z)

SVM 与 LR 的区别

  1. LR是参数模型，SVM是非参数模型
  2. 从目标函数来看，区别在于逻辑回归采用的是logistical loss（二分类，logistic loss就是 cross entropy: L = -( y1 * log(y1_hat) + y2 * log(y2_hat) ) 在 y1 + y2 = 1时的化简），SVM采用的是hinge loss。这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。
  3. SVM的处理方法是只考虑支持向量，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重。
  4. 逻辑回归相对来说模型更简单，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些。
  5. logic 能做的 svm能做，但可能在准确率上有问题，svm能做的logic有的做不了。

其他

  • LR 对异常值敏感、SVM 对异常值不敏感。支持向量机改变非支持向量样本并不会引起决策面的变化，逻辑回归中改变任何样本都会引起决策面的变化。如果我们在 LR 中使用核函数计算，那么每个样本都必须参与核计算，这带来的复杂度是非常高的。而 SVM 中只有少数几个代表支持向量的样本进行了计算
  • SVM 只考虑局部的边界线附近的点（支撑向量），而逻辑回归考虑全局（远离的点对边界线的确定也起作用，虽然作用会相对小一些）。
  • LR模型找到的那个超平面，是尽量让所有点都远离他，而SVM寻找的那个超平面，是只让最靠近中间分割线的那些点尽量远离，即只用到那些支持向量的样本。

https://www.jianshu.com/p/c49f8ae4cc53

SVM如何处理多分类问题？

间接法：对训练器进行组合。其中比较典型的有一对一，和一对多。

1）一对多： 对每个类都训练出一个分类器，由svm是二分类，所以将此而分类器的两类设定为目标类为一类，其余类为另外一类。这样针对k个类可以训练出k个分类器。

2）一对一： 针对任意两个类训练出一个分类器，如果有 k 类，一共训练出 C2k 个分类器。新样本每当被判定属于某一类时，该类就加一，最后票数最多的类别被认定为该样本的类。

KKT

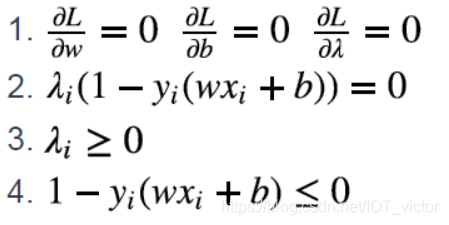
核函数

当样本在原始空间线性不可分时，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。而引入这样的映射后，所要求解的对偶问题的求解中，无需求解真正的映射函数，而只需要知道其核函数。

核函数的定义：K(x,y)=<ϕ(x),ϕ(y)>，即在特征空间的内积等于它们在原始样本空间中通过核函数 K 计算的结果。一方面数据变成了高维空间中线性可分的数据，另一方面不需要求解具体的映射函数，只需要给定具体的核函数即可，这样使得求解的难度大大降低。

  • 当特征维数  超过样本数  时 (文本分类问题通常是这种情况), 使用线性核;
  • 当特征维数  比较小. 样本数  中等时, 使用RBF核;
  • 当特征维数  比较小. 样本数  特别大时, 支持向量机性能通常不如深度神经网络

优缺点

优点

  • 由于SVM是一个凸优化问题，所以求得的解一定是全局最优而不是局部最优。

  • 不仅适用于线性线性问题还适用于非线性问题(用核技巧)。

  • 拥有高维样本空间的数据也能用SVM，这是因为数据集的复杂度只取决于支持向量而不是数据集的维度，这在某种意义上避免了“维数灾难”。

  • 理论基础比较完善(例如神经网络就更像一个黑盒子)。

缺点

  • 二次规划问题求解将涉及m阶矩阵的计算(m为样本的个数), 因此SVM不适用于超大数据集。(SMO算法可以缓解这个问题)

  • 只适用于二分类问题。(SVM的推广SVR也适用于回归问题；可以通过多个SVM的组合来解决多分类问题)看了

各模型的优缺点 https://blog.youkuaiyun.com/mach_learn/article/details/39501849

1 Linear SVM

1.1 SVM基本型

间隔最大化，求最优分离超平面

最条件的最优化问题（最大化间隔d）

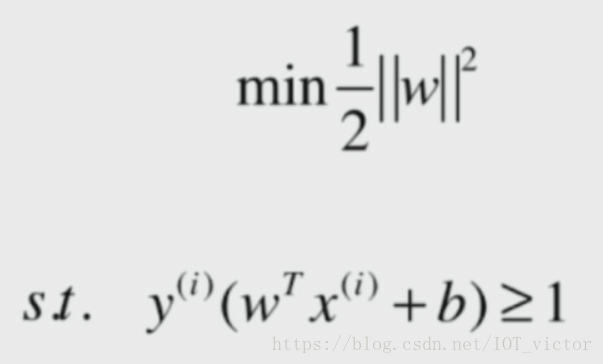
其中，||w||^{2}代表w二范数的平方

所以SVM基本型为：

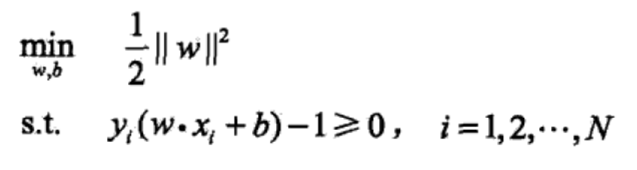
支持向量机是求解凸二次规划（目标函数是二次函数，约束函数是仿射函数）的最优化算法。

凸优化问题的标准形式为：

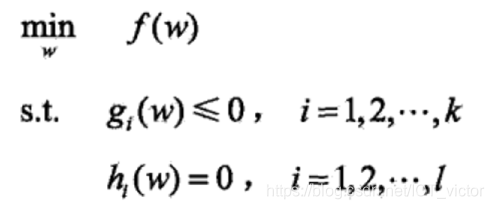
1.2 对偶问题

应用拉格朗日对偶性，通过求解对偶问题（dual problem）得到原始问题的最优解，这样更易求解，且可以自然引入核函数。

满足KKT条件（强对偶关系），先极大再极小（min （max L）），转换成 先对w，b求极小，再求 对拉格朗日乘子的极大。

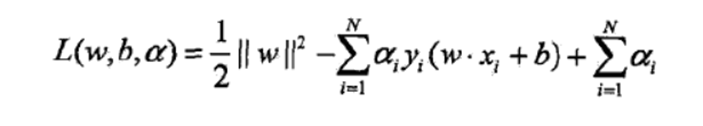
①求L 对 w，b求极小

                        

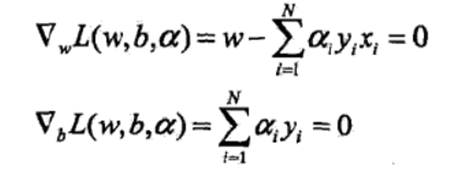
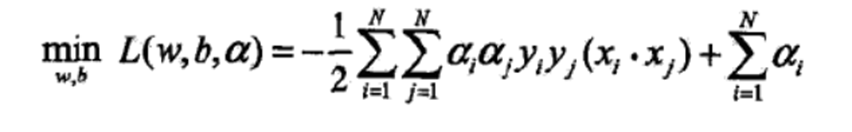
②求min L 对α的极大

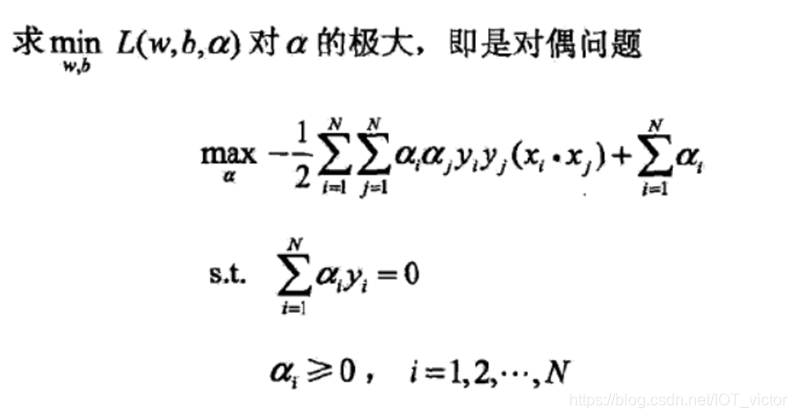
③构造并求解约束优化问题（序列最小最优化SMO算法求解最优解α^{*}\alpha ^{*}）

SMO算法的基本思路是每次选择两个变量，选取的两个变量所对应的样本之间间隔要尽可能大，因为这样更新会带给目标函数值更大的变化。

 

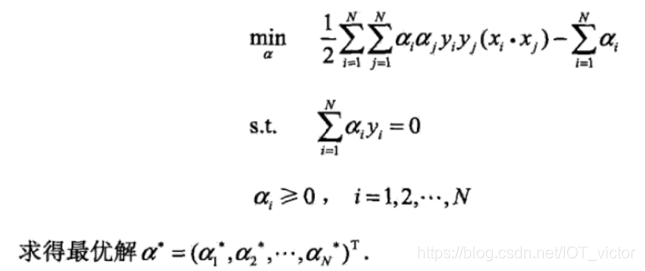
④计算最优w^{*} 和 b^{*}

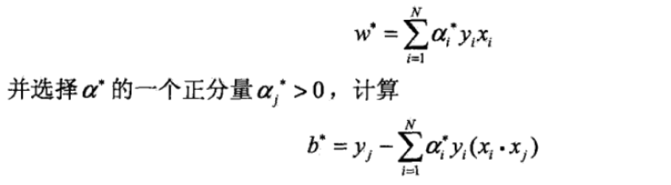
⑤求得分离超平面和分类决策函数

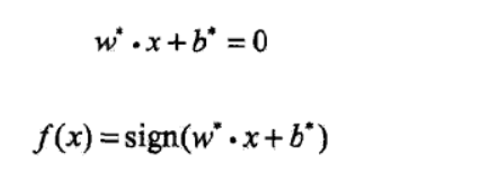
1.3 Soft Margin SVM

 

 

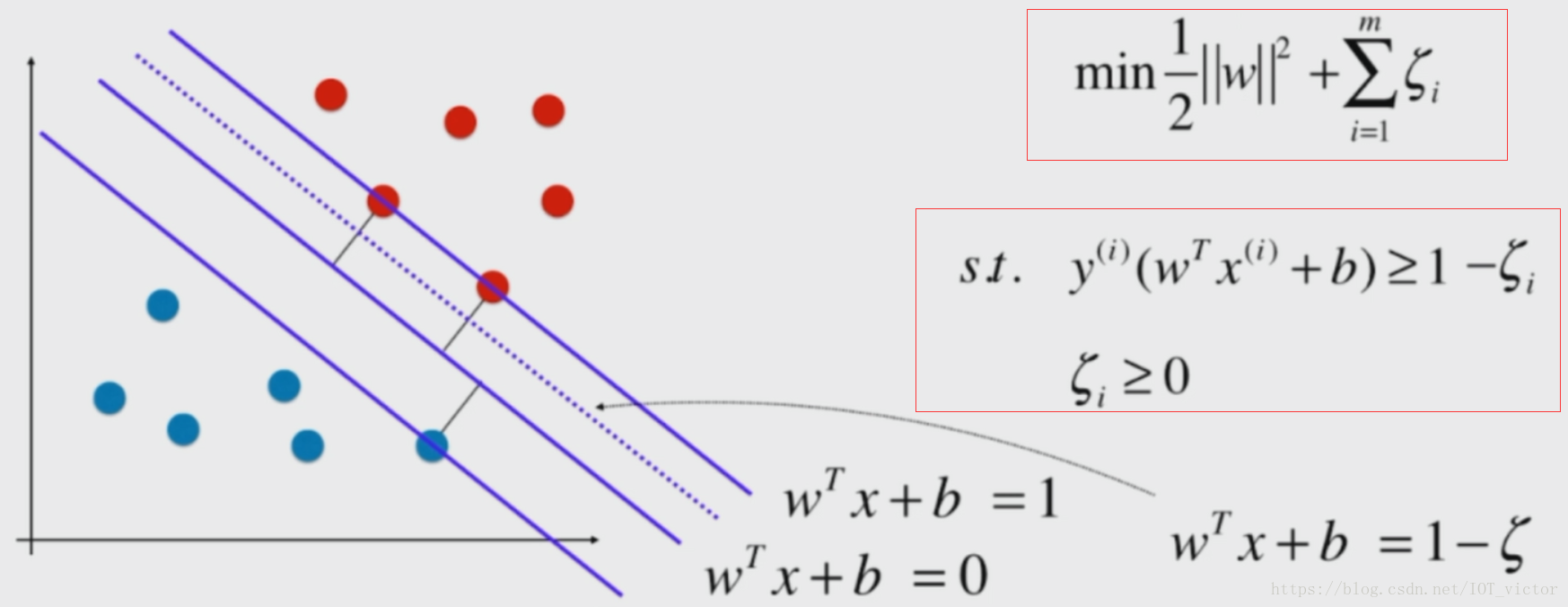
正则化

 

参考资料

[1] 《统计学习方法》李航

[2] 《Python3入门机器学习 经典算法与应用》liuyubobobo

[3] https://mp.weixin.qq.com/s/j_LzPcESaou0FOS2Z4f3kA

 

 

 

 

 

深度学习笔记——优化算法、激活函数
haopinglianlian的博客
11-21 2134
本笔记介绍深度学习中常见的优化算法、激活函数。
机器学习笔记——感知机、多层感知机(MLP)、支持向量机(SVM)
最新发布
haopinglianlian的博客
11-17 1806
本笔记介绍机器学习中的感知机、MLP、SVM算法。
支持向量机（SVM）之超平面（Hyperplane）
m0_51200050的博客
06-15 2346
支持向量机（SVM）之超平面（Hyperplane）
机器学习模型——SVM（支持向量机）
qq_60688380的博客
03-30 1711
SVM，即支持向量机（Support Vector Machine），是一种用于分类和回归分析的机器学习算法。线性分类器：SVM的基础是一个线性分类器，这意味着它通过在特征空间中绘制一条直线来区分不同的类别。在二维空间中，这条线就是一条直线；在三维空间中，它变成了一个平面；在更高维的空间中，它是一个超平面。最大间隔：SVM的一个特点是它试图找到最佳的分界线，使得两个类别之间的间隔（距离）尽可能大。这个间隔被称为“最大边距”，这样做的目的是为了确保分类的准确性和可靠性。支持向量。
SVM支持向量机
qq_20386411的博客
10-08 941
SVM支持向量机 可以做分类（经典的二分类问题）也可以做回归 如上图，不能找到一个边界将×和○分开？可以使用核函数，将数据映射到高维进行分割 边界都必须是直线吗？可以是直线也可以是平面‘ 无论选哪一个决策面，支持向量（雷区点）都不会改变（作垂线可以很清楚的发现），从而就涉及到下面的第一步，找点 决策边界：是中间的那条实线，不是雷区边界线 选择的决策边界是② ...
周志华《机器学习》西瓜书 小白Python学习笔记（七） ———— 第六章 支持向量机SVM
River_J777的博客
07-19 773
周志华《机器学习》西瓜书 小白Python学习笔记（七） ———— 第六章 支持向量机SVM什么是SVMSVM求解过程转化为Lagrange对偶问题Lagrange对偶问题求解1.min⁡w,bL(w,b,α)\min _{\boldsymbol{w}, b} L(\boldsymbol{w}, b, \boldsymbol{\alpha})minw,b​L(w,b,α)2. max⁡αi{min⁡w,bL(w,b,α)}\max_{\alpha_i}\{\min _{\boldsymbol{w},
机器学习笔记——SVM丝滑推导及代码实现，从硬间隔到软间隔再到核函数
andrew_1219的博客
06-01 1085
开始搓延期了一百年的机器学习实验，把SVM推导过程从定义到求解都刷了一遍，包括推导优化目标、提出对偶问题、利用KKT条件得到原问题的解以及SMO算法等
机器学习笔记——支持向量机（3）——原问题和对偶问题
weixin_45669062的博客
08-11 3589
引言 在上一节我们介绍了支持向量机svm解决非线性相关的问题。如何利用已知的K和未知的ψ去解决优化问题是关键。在这一节将针对原问题原对偶问题进行学习。 优化理论 原问题（Prime Problem） 最小化：f （ω） 限制条件：① gi（ω）<=0 ( i=1~K )；② hi（ω）=0 （ i=1~M ） 原问题是一个非常普适（general）的定义。 首先，最小化中 ω 是自变量，同时也是向量，待优化参数的自变量。f 是其函数。对于最小化的 f（ω），有最大化的 - f (ω）。 而在限制
支持向量机SVM
11-25
最近在研究人工智能，收集了一些好的资料，分享出来……也挣点积分，方便下次使用.
SVM:支持向量机
SZU_Hadooper的博客
07-22 501
支持向量机SVM目的最优的超平面点到平面的距离支持向量推理支持向量机求解支持向量机的对偶形式核技巧 SVM目的 低纬到高维，使线性不可分变成超平面下线性可分，SVM可以得到最优的超平面 最优的超平面 是指模型可以容忍最大的误差（灰色区域是高斯噪音，从第三个图可以看出高斯噪音的方差最大，模型的鲁棒性最好） 在SVM中就是找出margin最大的超平面 点到平面的距离 一个平面：w1x1+w2x2+....
SVM（支持向量机）
一般路过底层打工人的博客
10-20 990
支持向量机(Support Vector Machine,SVM)，可以用来解答二分类问题。：把划分数据的决策边界叫做超平面，点到超平面的距离叫做。在SVM中，距离超平面最近的且满足一定条件的几个训练样本点被称为支持向量。图中，被圈出来的就是支持向量。支持向量机是要使超平面和支持向量之间的间隔尽可能的大，这样才能使两类样本尽可能地分开。间隔又分为和。硬间隔存在的问题：1.只在数据线性可分时有效 2.对异常值非常敏感。
SVM(支持向量机)
coffee_fighter的博客
06-05 307
分类 监督学习、分类问题 算法原理 当样本线性可分的时候，寻找能切分样本并且最大间距的一个直线、平面或者超平面。 当样本非线性可分的时候，通过核函数映射到高维空间种，让样本线性可分。 代码实现 样本线性可分的情况： from sklearn import svm x=[[2,0],[1,1],[2,3]]#样本特征 y=[0,0,1]#样本标签 clf = svm.SVC(kernel = "li...
SVM 支持向量机
weixin_44177594的博客
03-30 3415
SVM支持向量机SVM1. SVM分类：2. Hand-Margin SVM3.Soft-margin SVM4. Kernel-Margin SVM4.1 核方法5.其他关于SVM？SVM对偶？SVM核技巧？SVM的物理意义是什么？SVM和全部数据有关还是和局部数据有关?SVM与LR的区别? SVM SVM；Support Vector Machine；支持向量机 1. SVM分类： hand-margin SVM 硬间隔 Soft-Margin SVM 软间隔 Kernel-Margin SVM
机器学习（三）——SVM支持向量机
林小川的博客
10-15 660
主要内容： SVM基本原理，带松弛因子的SVM，核方法，支持向量回归 基本原理： ①最大间隔原则：最大化两个类最近点之间的距离，该距离成为间隔（margin），边缘上的点为支持向量（support vectors），如下图所示：        设线性分割面如上有图所示：，根据向量的计算规则，可以得到： 带入求解可以得到：其中，x=0时，表示原点到分类面的距离       最...
过拟合与过拟合的经典例子
ywj_1991的博客
10-17 1148
本节通过概念解析与可视化例子，讲述什么是过拟合什么是过拟合过拟合是指在由于过度拟合训练数据，导致模型过于复杂，以致于在测试数据上预测效果不好正因此，过拟合也称为缺失泛化能力过拟合例子常用于解析过拟合的有两个例子曲线拟合可以看到，过拟合时，模型虽然在训练数据上拟合得更好，但拟合出的曲线已经偏离了原本形态平面分类可以看到，过拟合时，模型虽然在训练数据上达到更好的效果，但这种"更好的效果"是通过"勉强而为之"换取而来的，它对模型真实应用时有害无益。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值