基于IEEE33节点的配电网重构，采用 优流法开展了配电网重构工作，得到重构方案，应打开的开

基于IEEE 33节点配电网重构的实践分析：采用最优流法实现电力网优化

一、引言

随着电力的日益复杂化，配电网重构成为提高供电可靠性和经济性的重要手段。本文将围绕IEEE 33节点的配电网重构工作展开，采用最优流法进行配电网重构，探讨其工作流程、算法实现以及前后对比分析。

二、配电网重构的基本概念与流程

配电网重构是指在满足供电需求和安全运行的前提下，通过调整网络结构，优化网络布局，以降低网损、提高供电可靠性和电压质量。其中，最优流法是一种常用的配电网重构方法。

三、基于IEEE 33节点的配电网重构工作

1. 数据准备与初始化
   在进行配电网重构之前，需要准备相关数据，包括节点个数、支路参数、节点参数等。节点类型分为平衡节点、PQ节点等，这些数据为后续计算提供基础。

2. 采用最优流法进行潮流计算
   程序通过使用牛顿-拉夫逊法（Newton-Raphson method）进行迭代计算，寻找节点电压和功率的平衡。在这个过程中，程序不断调整网络中的开关状态，以实现最优的潮流分布。

四、最优流法的具体实现

1. 定义支路参数与节点参数
   支路参数包括支路电阻、电抗、变压器变比和电纳等，这些参数直接影响着电力的潮流分布。节点参数则包括注入有功、注入无功、电压幅值和电压相位等，它们反映了节点的电力需求和供电情况。

2. 牛顿-拉夫逊法迭代计算
   程序通过牛顿-拉夫逊法进行迭代计算，不断调整网络中的电压和功率分布，直到达到平衡状态。在这个过程中，程序会计算出应打开的开关数，以实现最优的潮流分布。

五、重构方案与结果分析

通过上述流程，我们得到了基于IEEE 33节点的配电网重构方案。该方案包括应打开的开关数以及对应的网络结构调整方案。同时，我们对比了重构前后的网损和电压结果。

六、前后对比分析

1. 网损对比
   通过配电网重构，我们有效降低了的网损。重构后的网损明显低于重构前，这表明我们的优化措施取得了显著成效。

2. 电压结果对比
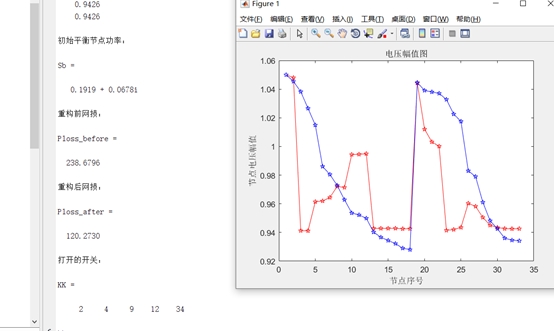
   在电压方面，配电网重构也带来了明显的改善。重构后，的电压质量得到了提高，电压波动得到了有效控制。

七、结论

本文围绕IEEE 33节点的配电网重构工作展开，采用最优流法进行配电网重构。通过数据准备与初始化、采用牛顿-拉夫逊法进行潮流计算等步骤，我们得到了重构方案以及应打开的开关数。同时，我们对比了重构前后的网损和电压结果，发现配电网重构在降低网损和提高电压质量方面取得了显著成效。这为电力运行管理和优化提供了有力支持。未来，我们将继续深入研究配电网重构技术，以更好地满足电力的需求。
基于IEEE33节点的配电网重构，采用最优流法开展了配电网重构工作，得到重构方案，应打开的开关数等，同时对比了重构前后的网损和电压结果
–以下内容来源于第三方解读，仅供参考
这段代码是一个用于电力潮流计算的程序。它使用了牛顿-拉夫逊法（Newton-Raphson method）来迭代计算节点电压和功率的平衡。下面我会逐步解释代码的功能和算法。

首先，代码定义了一些变量和数据，包括节点个数、支路参数、节点参数等。其中，节点类型分为平衡节点、PQ节点、PV节点和PI节点。支路参数包括支路电阻、电抗、变压器变比和电纳。节点参数包括注入有功、注入无功、电压幅值和电压相位。

代码的主要部分是一个while循环，用于进行潮流计算的迭代。循环中的代码包括以下几个步骤：

计算节点导纳矩阵Y：根据支路参数计算节点之间的导纳矩阵Y。导纳矩阵是一个复数矩阵，表示节点之间的导纳关系。

初始化节点功率参数OrgS：根据节点类型和参数，计算初始的有功功率和无功功率。

创建DetaS：根据节点类型和参数，计算初始的有功功率、无功功率和电压幅值的不平衡量。

创建Jacbi矩阵：根据节点参数和导纳矩阵，计算雅可比矩阵。雅可比矩阵是一个复数矩阵，表示节点电压和功率之间的关系。

求解修正方程：使用雅可比矩阵和DetaS，通过求解线性方程组，得到节点电压的修正量DetaU。

修正节点电压：根据修正量DetaU，更新节点电压。

判断是否达到收敛条件：通过比较修正量DetaU的绝对值与误差精度pr，判断是否达到收敛条件。如果未达到，则返回第3步继续迭代。

计算网损：根据节点电压和导纳矩阵，计算的有功损耗。

输出结果：输出迭代次数、节点电压幅值和网损。

这段代码的优势在于使用了牛顿-拉夫逊法进行迭代计算，可以较快地收敛到潮流平衡。它可以应用于电力潮流计算的各个领域，如电网规划、电网运行和电力市场等。通过分析这段代码，新手可以学到潮流计算的基本原理和方法，了解电力中节点电压和功率之间的关系，以及如何使用迭代方法求解非线性方程组