用Python做投资-python仿真等价鞅下的收益曲线

有一个赌局，抛一枚硬币，正面朝上赢，反面朝上输。然后每次自由下注。

如果我们按照这样的次序下注：1,2,4,8,16，......,2^n.只要有一次获胜，那么我们就从头再来。这里我们可以看出，每次获胜都可以赢得1元钱。因为2^n次方的数列前n-1次项和为2^n-1。这里我们就能看出，只要你有足够多的钱，那么你总能赚钱。这一游戏，就叫做等价鞅。

 

1. # -*- coding: utf-8 -*-

2. """

3. Created on Mon Oct 24 16:05:03 2016

4.  

5. @author: Luyixiao

6. """

7.  

8. import numpy as np

9. import matplotlib.pyplot as plt

10. import pandas as pd

11. # true = win;false = loss

12. def winOrLossGenerator(p,size):

13. randomNumber = np.random.uniform(0,1,size)

14. WL = randomNumber < p

15. return WL

16.  

17. def player(WL_list):

18. amount = 100#1$ as initial money

19. moneyList=[]#use this list to record the lost of the money amount

20. gain = 0

21. margin = 100

22. lossNumber = 0

23. for i in range(0,len(WL_list)):

24. #print WL_list[i]

25. if WL_list[i] == True:

26. lossNumber = 0

27. gain = gain + 1

28. margin = amount + gain

29.  

30. if WL_list[i] == False:

31. margin = margin - 2**lossNumber

32. lossNumber = lossNumber + 1

33. moneyList.append(margin)

34. print moneyList

35. fig = plt.figure(figsize=(10,20))

36. plt.title("win probability is 0.5")

37. plt.plot(range(0,len(moneyList)),moneyList)

38.  
39.  

40. WL_list = winOrLossGenerator(0.5,100)

41. #print WL_list

42. player(WL_list)

上面的代码用蒙特拉罗的思想模拟了这一游戏，

winOrLossGenerator

函数用于产生size个输或者赢的序列。

 

 

player(WL_list)

函数则用于模拟赌博的人。每次运行的结果都是不一样的，我们取一次观察一下资金的变化情况。

 

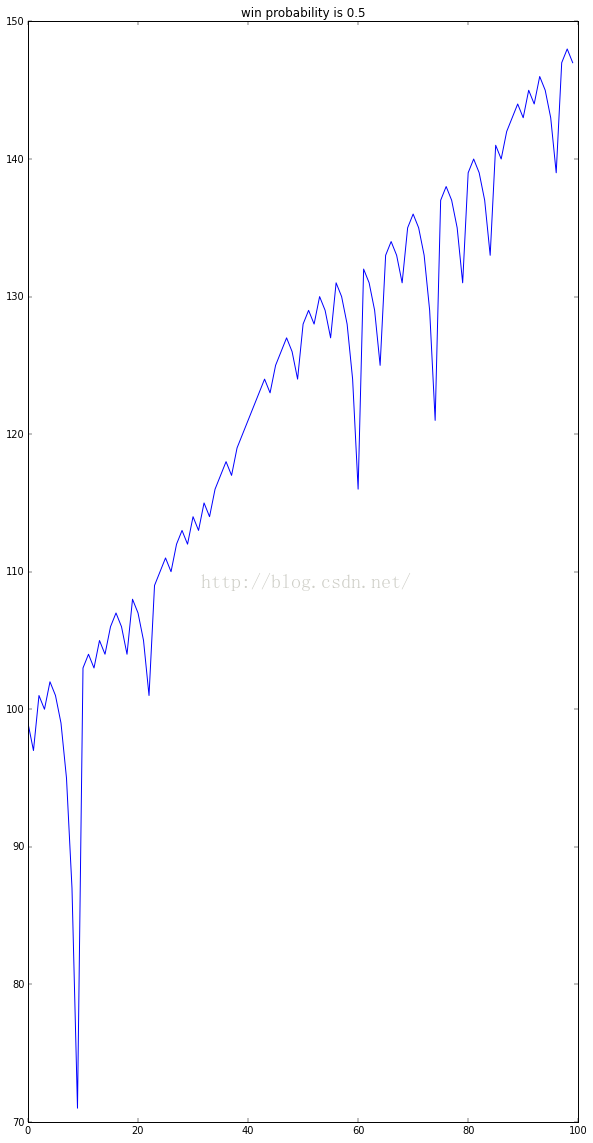
我们可以看到，这次仿真中，最大的资金回测大概在72元左右。我们修改一下获胜的概率，假设我们的硬币是不均匀的，而赌场中往往是这呀。

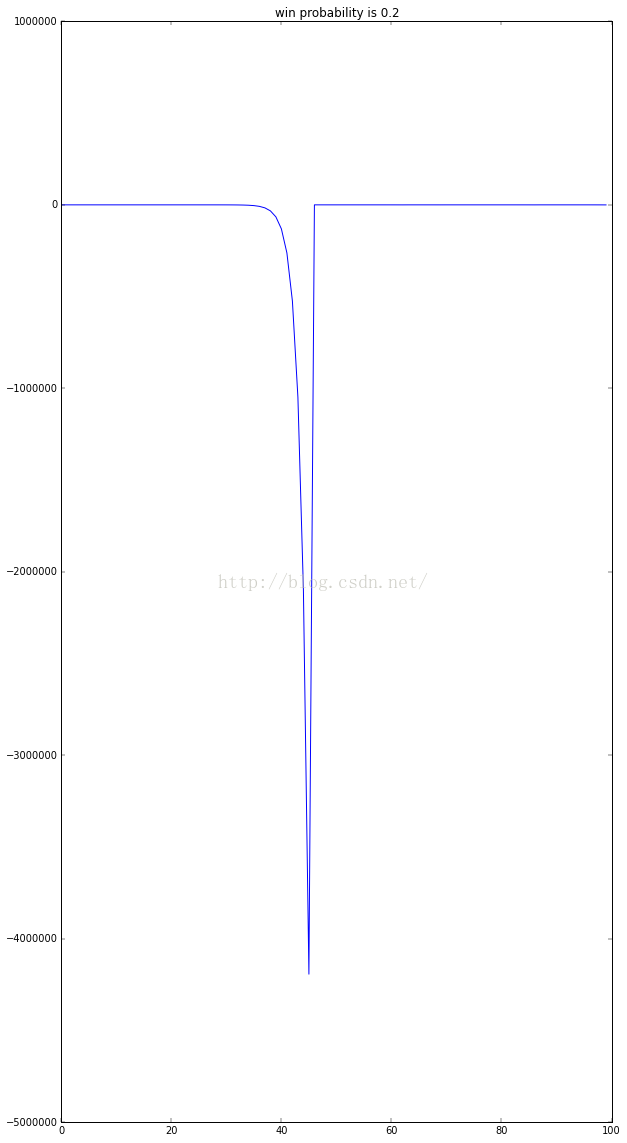
如果我们的获胜概率只有2，那么资金曲线是这样的：

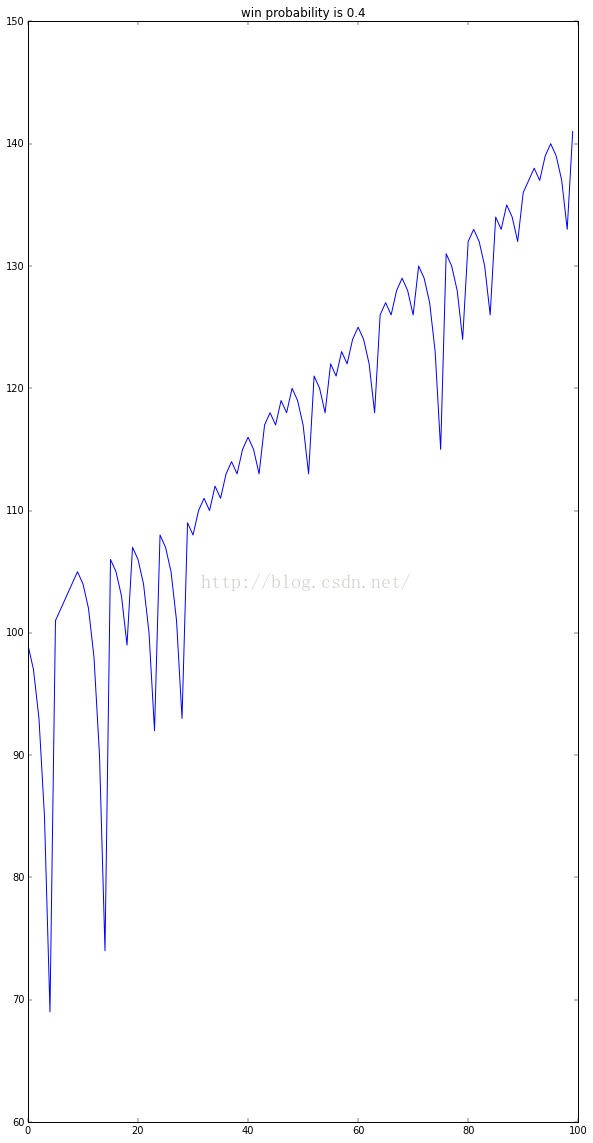
获胜率为0.4，情况还马马虎虎

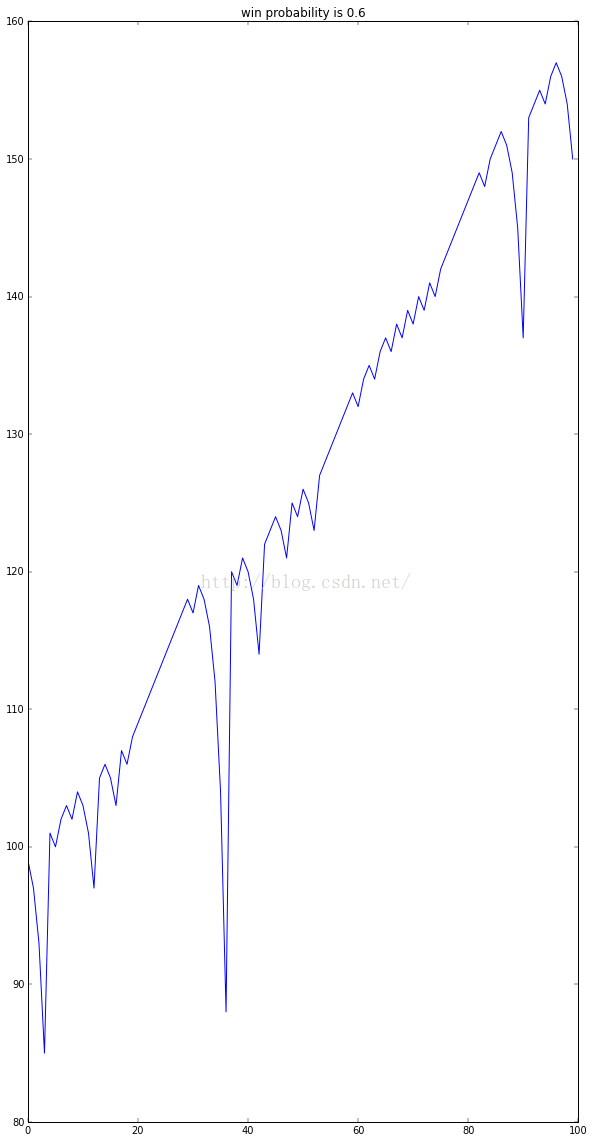
获胜的概率为0.6：

获胜的概率为0.9的时候，资金曲线就比较平稳的向上了：

 

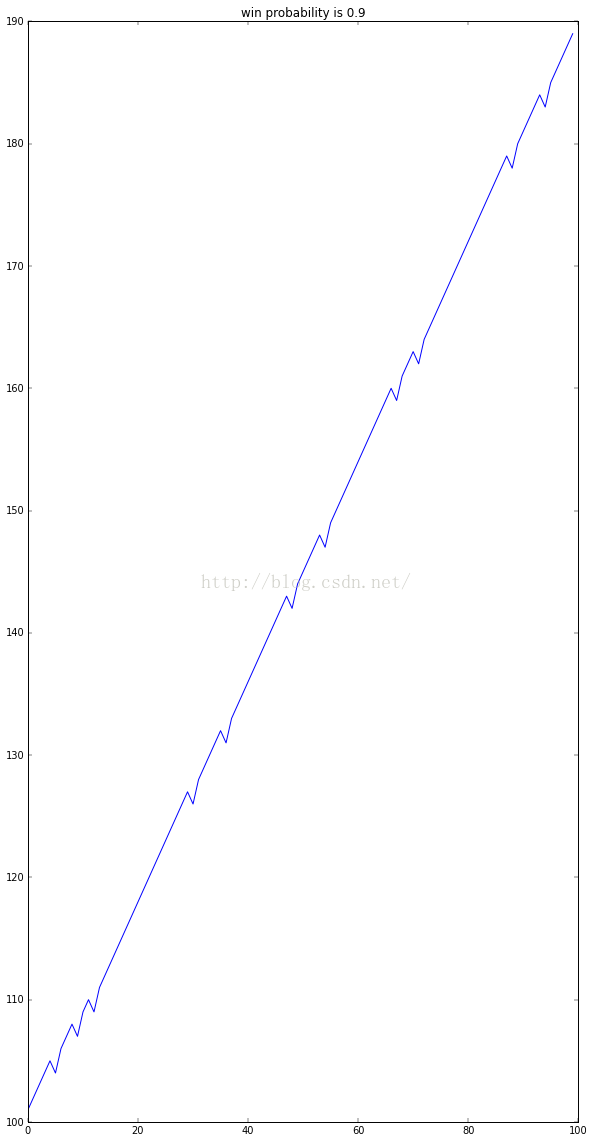
--------------------- 本文来自 钱塘小甲子 的优快云 博客 ，全文地址请点击：https://blog.youkuaiyun.com/qtlyx/article/details/52913977?utm_source=copy