GCN笔记

上一个帖子就算给GNN简单开了个头，现在开始对GNN下的具体策略进行讲述。

1.GCN简介

GCN是一种在图（graph）上进行信息聚合的算法，基于谱域或者空域

1.1基于谱域的GCN

在基于谱域的GCN中，其公式类似于CNN中有卷积核以及被卷积数据，因此得名GCN。在GCN中卷积核与数据进行一次卷积运算即可聚合每一个节点的邻域信息。因此GCN是作用于整个图数据上的，每一次图卷积运算之后，所有节点都被处理完毕（计算量大），但是其弊端也在于每次必须处理整张图，如果图中新加入了一个节点，那么卷积核便需要重新运算。

1.2基于实域的GC空

在基于实域的GCN中，卷积操作并非是卷积核乘以图数据，而是以某种采样策略作用于特点节点上。比如GraphSage，这种策略如果想求某一结点的embedding不必处理整个图。

2.基于谱域的GCN

2.1公式

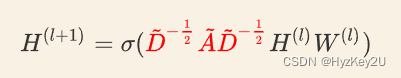
红色部分即为卷积算子——对称标准化拉普拉斯矩阵

2.2拉普拉斯矩阵

从公式看，先不考虑拉普拉斯矩阵，A*H其实就是聚合邻域信息，Ahead是A+I，相当于将自身信息聚合到自身，免去聚合邻域之后再自加的过程。其实也完成了聚合邻域的过程，但是这种算法不区分结点本身的特色，若某节点度很大，那么它对整个系统的影响也是很大的（度*embedding），不可否认这个结点在系统中很重要，信息量很大，但是由于度很大，因此它分给邻居的信息不应该是其本身，而应该是其的一部分。因此应该将度纳入考虑之中。

对称式标准化拉普拉斯矩阵由邻接矩阵A+单位阵（表示self-loop）左乘、右乘度矩阵的负二分之一次方（D为对角阵，因此直接对对角线的数字开方再取倒数即可，并且矩阵左乘右乘初等矩阵等于在矩阵上做同样的初等变换，可以用手模拟算一下）。标准化后的拉普拉斯矩阵作为图卷积算子更为合理。