《信息系统项目管理师教程》计算题

原创已于 2025-12-09 10:54:58 修改 · 28 阅读

·

0

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

于 2022-03-25 23:01:10 首次发布

信息系统项目管理师专栏收录该内容

1 篇文章

订阅专栏

选择题类型

解： $(300-100)*75%+(60-100)*25% =200*75%-40*25% =150-10 =140$

（1）解： $(7+8+9)*20%=1.6$

（2）解：选C

系统A： $90*40%+80*40%+80*20%=84$

系统B： $80*40%+85*40%+90*20%=84$

解：C

自制： $12*800+4000=9600+4000=13600$

采购： $17*800=13600$

（1）共同渠道计算公式： $\frac{N(N-1)}{2}=\frac{5*4}{2}=10$

数量级： $N^{2}$ （死答案，不会变）

（2）解： $\frac{20000}{4*5000-\frac{4*3}{2}*250}=\frac{20000}{18500}\approx 1.08$

（1）解： $\frac{110000}{(1+10%)}+\frac{121000}{(1+10%)^{2}}=100000+100000=200000$

（2）解：C，在初始投资额与回收期相同的情况下，净现值（NPV）越多越好

（7）解：C

至2006年未收回来的钱： $-925.93+428.67+396.92=-100.34$

2007年还需要的动态投资回收期： $100.34/367.51\approx 0.27$

动态投资回收期： $2+0.27=2.27$

（8）解：B

$\frac{1}{2.27}=44%$ ；投资收益率反映企业投资的获利能力，等于动态回收期的倒数。

（69）解：A

$\frac{2000-990}{1210}+1\approx 1.83$

（70）解：B

2007年贴现： $\frac{990}{1+10%}=900$

2008年贴现： $\frac{1210}{(1+10%)^{2}}=1000$

2009年贴现： $\frac{1198}{(1+10%)^{3}}\approx 900$

$\frac{2000-900-1000}{900}+2\approx 2.1$

$T_{1}=\frac{T_{2}+T_{3}+4T_{4}}{6}$

标准差 =（悲观时间 - 乐观时间）/ 6

（1）解：B

$\frac{6+36+4*21}{6}=21$

标准差： $\frac{36-6}{6}=5$

$\frac{68.3%}{2}=34.15%$

（2）解：B、B

$\frac{8+38+4*20}{6}=21$

标准差： $\frac{38-8}{6}=5$

$50%-\frac{68.3%}{2}=50%-34.15%\approx 15.9%$

（3）解：A

$\frac{12+36+4*21}{6}=22$

标准差： $\frac{36-12}{6}=4$

选择题与案例分析

总时差 = 最迟开始 - 最早开始 = 最迟结束 - 最早结束

自由时差 = 紧后的最早开始 - 此活动的最早结束；若任务没有紧后任务，则自由时差 = 总时差

注：关键活动的总时差、自由时差都是 0，一张图中可能有多个关键路径

单代号网络图是由节点和箭线组成的，其箭线表示紧邻工作之间的逻辑关系，节点则表示工作。

双代号网络图能够清楚地展现计划的时间进程。直接显示各项工作的开始与完成时间、工作的自由时差和关键线路。

（1）解：D

总时差 = $13 - 3 = 19 - 9 = 10$

（2）解：B

总时差 = $8-6=2$

（3）解：C

$60%*60%*60%=21.6%$

（4）解：C、A

（5）解：D（双代号网络图）

1 → 3 → 5 → 6 → 8：2 + 7 + 6 + 3 = 18

（6）解：D

D → H → C：9 + 0 + 3 = 12

12 - 8 = 4

（7）解：A（⑤ → ⑥的虚线：虚工作，虚工作可以在关键路径上）

① → ② → ③ → ④ → ⑤ → ⑥ → ⑧ → ⑨：3 + 5 + 0 +7 +0 + 2 + 2 = 19

19 - 17 - 2 = 0

【问题1】

（1）解：最早开始时间、最早结束时间从前往后做加法，最迟开始时间、最迟结束时间从后往前做减法

（2）解：

关键路径：A → C → D → G → H

工期：5 + 8 + 10 + 11 + 10 = 44

【问题2】解：压缩关键活动

关键活动中压缩 A 需要 5 万元、压缩 C 需要 3 万元、压缩 D 需要 2 万元、压缩 G 需要 5 万元、压缩 H 需要 8 万元。

故压缩 C 和 D 所增加的费用最小：3 + 2 = 5（万元）

【问题3】解：事件2中通过压缩关键路径所增加的费用为 5 万元，压缩 2 天节省 2 万元，甲方额外支付8万元的项目款。

故：8 - 5 + 2 = 5（万元）利润因工期提前增加了5万元。

（9）解：C

最短时间内完成：7天

活动 A 可延后 5 天，活动 C 可延后 2 天。

活动 B 与活动 C 同时开始，活动 C 完成后，将员工调往活动 A ，故至少需要4 + 3 人。

（10）解：A、B（可直接选次小项）

关键路径：A → C → E → G → H：2 + 1 + 2 + 2 + 1 = 8

（11）

【问题1】解：

关键路径：A → C → D → H

项目完成至少需要：5 + 3 + 4 + 5 = 17周

【问题2】解：

B的总时差：画图，可用关键路径 - 通过B到终点的最长路径 = A → C → D → H - B → C → D → H = 17 - 13 = 4

G的总时差：关键路径 - 通过G到终点的最长路径 = A → C → D → H - A → C → D → G = 17 - 15 = 2

B的自由时差：F 的最早开始时间 - B 的最早结束 = 1 - 1 = 0

G的自由时差：G 没有紧后任务，G 的自由时差 = G的总时差 = 2

（12）双代号时标网络图，起点到终点中没有波浪线的就是关键线路。

【问题1】

（1）解：

关键路径：B → D → E → G

工期：24

（2）解：

名称：双代号时标网络图

可以表示进度计划的图：前导图、里程碑计划图、甘特图

（3）解：

任务的总时差：就是以该任务为起点到终点，可能有多条的线路，每一条线路的波浪线的长度的和的最小值，就是总时差
自由时差：波浪线的长度

A 任务的总时差：A → C → E → G 的波浪线的和：3

D 任务的总时差：D → E → G 的波浪线的和：0

F 任务的总时差：F 的波浪线的和：7

A 的自由时差：2

D 的自由时差：0

F的自由时差：7

（4）解：

C 的总时差：C → E → G 的波浪线的和：1，所以没有影响

挣值： $EV$ ，又称实现价值。顾名思义，指的就是“已经完成工作的价值”。

计划价值： $PV$ ，开始点到检查点一个完成的工作量1。

实际成本： $AC$

完成预算： $BAC$

成本偏差： $CV=EV-AC$ ；＞0，节省；＜0，超支

进度偏差： $SV=EV-PV$ ；＞0，提前；＜0，滞后

成本绩效指数： $CPI=EV/AC$ ；＞1，节省；＜1，超支

进度绩效指数： $SPI=EV/PV$ ；＞1，提前；＜1，滞后

非典型偏差的完工尚需估算： $ETC=(BAC-EV)$

典型偏差的完成尚需估算： $ETC=(BAC-EV)/CPI$

完工估算： $EAC=AC+ETC$

非典型偏差的完工估算： $EAC=AC+BAC-EV$

典型偏差的完工估算： $EAC=AC+(BAC-EV)/CPI$

完工偏差： $VAC=BAC-EAC$

图（1）成本偏差 CV < 0，成本超支，进度偏差 SV < 0，进度滞后

图（2）成本偏差 CV = 0，成本持平，进度偏差 SV < 0，进度滞后

图（3）成本偏差 CV = 0，成本持平，进度偏差 SV > 0，进度提前

图（4）成本偏差 CV > 0，成本节省，进度偏差 SV > 0，进度提前

（1）解：D

$SPI=EV/PC=300/375=80%$

（2）解：A

成本绩效指数 CPI > 0，成本节省

（3）解：C，如果当前偏差为典型偏差，这为比例关系

BAC：800，AC：200，EV：100，PV：400

两年超支： $CV = EV - AC = 100-200=-100$

当前偏差为典型偏差，四年超支 $2CV=2*(-100)=-200$

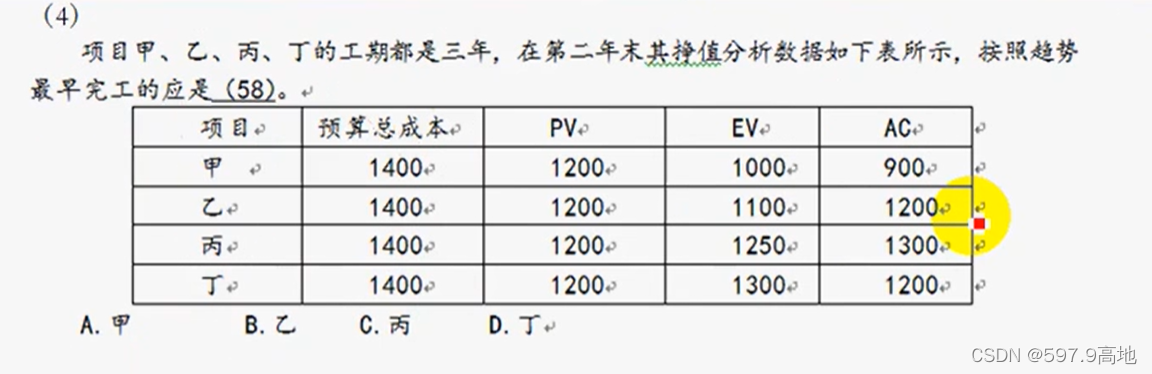
（4）解：D，丁的 SPI 值最大，这题无需计算，PV 值都相同，EV 越大，SPI值越大

甲： $SPI=EV/PV=1000/1200$

乙： $SPI=EV/PV=1100/1200$

丙： $SPI=EV/PV=1250/1200$

丁： $SPI=EV/PV=1300/1200$

（5）解：A

①： $EV-AC=CV$

②： $EV- AC = CV$ ，但是该时刻未竣工

③： $EV-PV=SV$

④：尚需工期

（6）

【问题1】解：

计划成本：PV，实际成本：AC，完成百分比：SPI

$EV= SPI*PV$

【问题2】解：

（7）

【问题1】解：

PV：2万元，EV：1万元，AC：8千元

$CPI=EV/AC =10000/8000=1.25$

$SPI =EV /PV=10000/20000=0.5$

【问题2】解：

【问题3】

（1）解：

$ETC= BAC-EV= 40000-10000=30000$

$EAC=AC+ETC=8000+30000=38000$

预测完工日期：3月21日

（2）解：

$ETC=(BAC-EV)/CPI=(40000-10000)/1.25=24000$

$EAC=AC+ETC=8000+24000=32000$

预测完工日期：3月24日

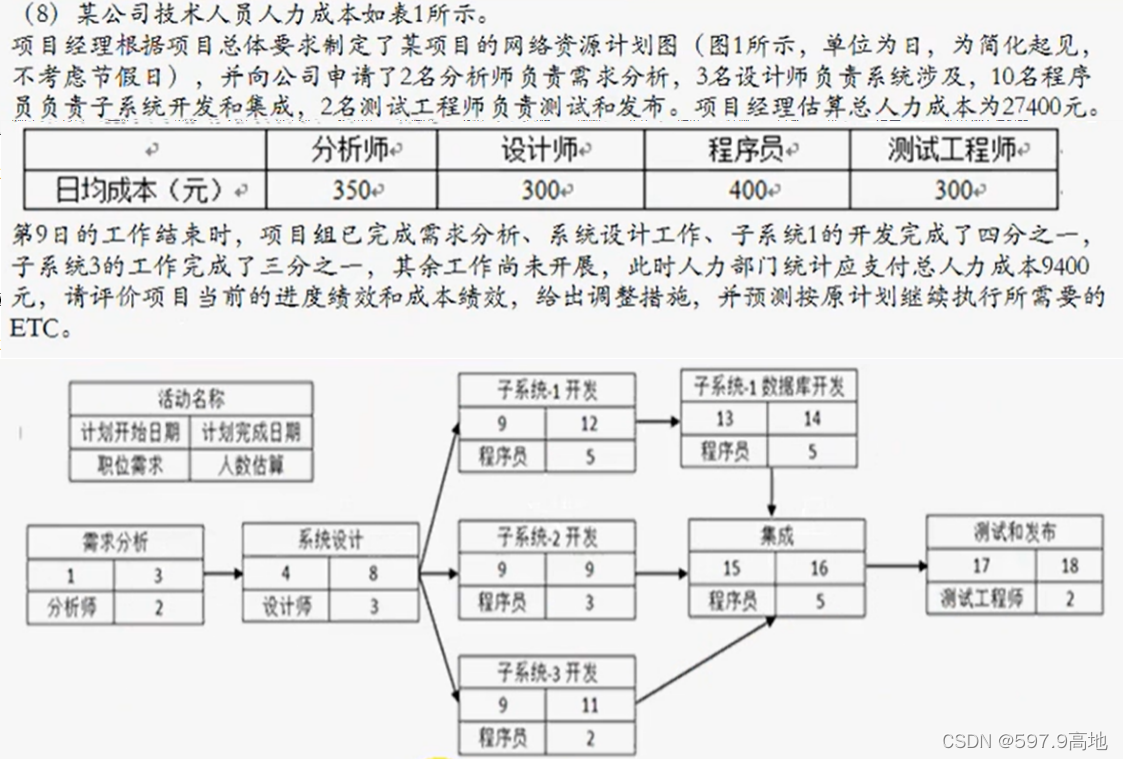
（8）解：AC：9400，BAC：27400

需求分析：350 * 2 * 3 = 2100

系统设计：300 * 3 * 5 = 4500

子系统 1 开发：400 * 4 * 5 = 8000

子系统 2 开发：400 * 1 * 3 = 1200

子系统 3 开发：400 * 3 * 2 = 2400

子系统 1 数据库开发：400 * 2 * 5 = 4000

集成：400 * 2 * 5 = 4000

测试与发布：300 * 2 * 2 = 1200

$EV=2100+4500+8000*\frac{1}{4}+2400*\frac{1}{3}=9400$

截止到第九天计划完成的工作量： $PV =2100+4500+\frac{1}{4}*8000+1200+\frac{1}{3}*2400=10600$

$CPI=EV/AC =1$ ，成本与预算持平，无需调整

$SPI=EV/PV=9400/10600=0.89$ ，进度落后

措施：用高效人员替代低效率人员、新技术、加班赶工

$ETC=BAC-EV=27400-10600=16800$

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。