冒泡排序
冒泡排序(Bubble sort)是一种交换排序。它的基本思想是:两两比较相邻记录的关键字,如果反序则交换,知道没有反序的记录为止。
首先介绍一个简单版本的冒泡排序算法的实现代码。
1 2 3 4 5 6 7 8 9 10 11 12 | // 冒泡排序初级版 void BubbleSort0(SqList *L){ int i, j; for (i = 0; i < L->length - 1; i++) { for (j = i + 1; j <= L->length - 1; j++){ if (L->r[i] > L->r[j]){ // 实现递增排序 swap(L, i, j); } } } } |
这段代码不算是标准的冒泡排序算法,因为不满足“两两比较相邻记录”的冒泡排序思想,它更应该是最简单的交换排序。它的思路是让每一个关键字都和后面的每一个关键字比较,如果大或小则进行交换,这样关键字在一次循环后,第一个位置的关键字会变成最大值或者最小值。
这个最简单的实现算法效率是非常低的。
下面介绍正宗的冒泡排序算法实现。
1 2 3 4 5 6 7 8 9 10 11 12 13 | // 正宗的冒泡排序算法实现代码 void BubbleSort(SqList *L){ int i, j; for (i = 0; i < L->length; i++) { for (j = L->length - 2; j >= i; j--){ // j是从后往前循环 if (L->r[j] > L->r[j + 1]){ // 实现递增排序 swap(L, j, j + 1); } } } } |
这里改变的地方是在内循环中,j是从数组最后往前进行比较,并且是逐个往前进行相邻记录的比较,这样最大值或者最小值会在第一次循环过后,从后面浮现到第一个位置,如同气泡一样浮到上面。
这段实现代码其实还是可以进行优化的,例如待排序数组是{2,1,3,4,5,6,7,8,9},需要进行递增排序,可以发现其实只需要交换前两个元素的位置即可完成,但是上述算法还是会在交换完这两者位置后继续进行循环,这样效率就不高了,所以可以在算法中增加一个标志,当有一次循环中没有进行数据交换,就证明数组已经是完成排序的,此时就可以退出算法,实现代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | // 改进版冒泡算法 void BubbleSortOptimz(SqList *L){ int i, j; bool flag = true; for (int i = 0; i < L->length && flag; i++){ // 若 flag为false则退出循环 flag = false; for (j = L->length - 2; j >= i; j--){ // j是从后往前循环 if (L->r[j] > L->r[j + 1]){ // 实现递增排序 swap(L, j, j + 1); // 如果有数据交换,则flag是true flag = true; } } } } |
冒泡排序算法的时间复杂度是




 O(n2)。
O(n2)。
完整的冒泡排序算法代码可以查看BubbleSort。
简单选择排序
简单选择排序算法(Simple Selection Sort)就是通过
n−i次关键字间的比较,从
n−i+1个记录中选出关键字中最小的记录,并和第
i(1≤i≤n)个记录进行交换。
下面是实现的代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | // 简单选择排序算法 void SelectSort(SqList *L){ int i, j, min; for (i = 0; i < L->length - 1; i++){ // 将当前下标定义为最小值下标 min = i; for (j = i + 1; j <= L->length - 1; j++){ if (L->r[j] < L->r[min]) min = j; } // 若min不等于i,说明找到最小值,进行交换 if (min != i) swap(L, i, min); } } |
简单选择排序的最大特点就是交换移动数据次数相当少。分析其时间复杂度发现,无论最好最差的情况,比较次数都是一样的,都需要比较
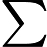
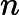


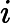





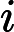












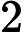
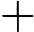


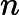
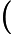
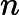


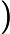
 ∑i=1n−1(n−i)=(n−1)+(n−2)+⋯+2+1=n(n−1)2次。对于交换次数,最好的时候是交换0次,而最差的情况是
∑i=1n−1(n−i)=(n−1)+(n−2)+⋯+2+1=n(n−1)2次。对于交换次数,最好的时候是交换0次,而最差的情况是


 n−1次。因此,总的时间复杂度是
n−1次。因此,总的时间复杂度是




 O(n2),虽然与冒泡排序一样的时间复杂度,但是其性能上还是略好于冒泡排序。
O(n2),虽然与冒泡排序一样的时间复杂度,但是其性能上还是略好于冒泡排序。
直接插入排序
直接插入排序(Straight Insertion Sort)的基本操作是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增加1的有序表。
实现代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | // 直接插入排序 void InsertSort(SqList *L){ int i, j,val; for (i = 1; i <= L->length - 1; i++){ if (L->r[i] < L->r[i - 1]){ // 将L->r[i]插入有序表中,使用val保存待插入的数组元素L->r[i] val = L->r[i]; for (j = i - 1; L->r[j]>val; j--) // 记录后移 L->r[j + 1] = L->r[j]; // 插入到正确位置 L->r[j + 1] =val; } } } |
直接插入排序算法是需要有一个保存待插入数值的辅助空间。
在时间复杂度方面,最好的情况是待排序的表本身就是有序的,如{2,3,4,5,6},比较次数则是


 n−1次,然后不需要进行移动,时间复杂度是
n−1次,然后不需要进行移动,时间复杂度是



 O(n)。
O(n)。
最差的情况就是待排序表是逆序的情况,如{6,5,4,3,2},此时需要比较$\sum{i=2}^{n} i = \frac{(n+2)(n-1)}{2} 次,而记录的移动次数也达到最大值 次,而记录的移动次数也达到最大值\sum{i=2}^{n} (i+1) = \frac{(n+4)(n-1)}{2}$次。
如果排序记录是随机的,那么根据概率相同的原则,平均比较和移动次数约为
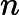
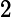
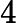 n24。因此,可以得出直接插入排序算法的时间复杂度是
n24。因此,可以得出直接插入排序算法的时间复杂度是




 O(n2)。同时也可以看出,直接插入排序算法会比冒泡排序和简单选择排序算法的性能要更好一些。
O(n2)。同时也可以看出,直接插入排序算法会比冒泡排序和简单选择排序算法的性能要更好一些。























 30万+
30万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








