动态规划之——跳跃游戏V

题意：

给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到：
i + x ，其中 i + x < arr.length 且 0 < x <= d 。
i - x ，其中 i - x >= 0 且 0 < x <= d 。
除此以外，你从下标 i 跳到下标 j 需要满足：arr[i] > arr[j] 且 arr[i] > arr[k] ，其中下标 k 是所有 i 到 j 之间的数字（更正式的，min(i, j) < k < max(i, j)）。
你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。
请注意，任何时刻你都不能跳到数组的外面。
示例 1：
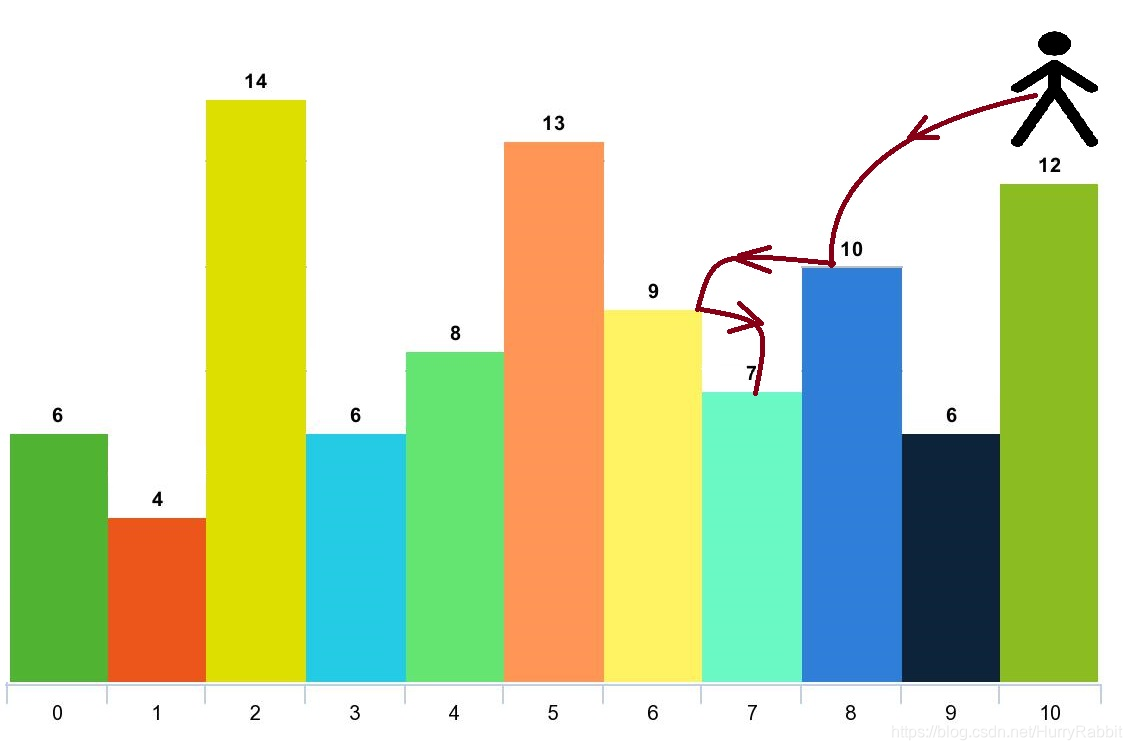
输入：arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出：4
解释：你可以从下标 10 出发，然后如上图依次经过 10 --> 8 --> 6 --> 7 。
注意，如果你从下标 6 开始，你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处，因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的，你不能从下标 3 处跳到下标 2 或者下标 1 处。

题目大意是给出一个数组，从这个数组中的任何一个位置开始起跳，横向距离不能超过d，目的地的值要小于当前的值，找出这个数组从一个节点可以最多跳多少次？

---

这个题目第一眼看到就想起了动态规划，设置一个dp数组，dp[i]表示从下标i起跳，最多可以到达的下标的次数。

max(dp[j]) + 1；

其中 j 需要满足三个条件：

0 <= j < arr.length，即j必须在数组 arr 的范围内；

i - d <= j <= i + d，即 j到i的距离不能超过给定的d；

从 arr[j]到 arr[i] 的这些元素除了 arr[i]本身之外，都必须小于 arr[i]，这是题目中的要求。

对于任意的位置 i，根据第二个条件，我们只需要在其左右两侧最多扫描 d 个元素，就可以找出所有满足条件的位置j。随后我们通过这些 j 的dp 值对位置i进行状态转移，就可以得到 dp[i] 的值。
此时出现了一个需要解决的问题，如何保证在处理到位置 i 时，所有满足条件的位置 j 都已经被处理过了呢？换句话说，如何保证这些位置 j 对应的 dp[j] 都已经计算过了？如果我们用常规的动态规划方法（例如根据位置从小到大或者从大到小进行动态规划），那么并不能保证这一点，因为 j 分布在位置 i 的两侧。
因此我们需要借助记忆化搜索的方法，即当我们需要 dp[j] 的值时，如果我们之前已经计算过，就直接返回这个值（记忆）；如果我们之前没有计算过，就先将 dp[i] 搁在一边，转而去计算 dp[j]（搜索），当 dp[j] 计算完成后，再用其对 dp[i]进行状态转移。

以下是代码：

class Solution {
private:
    vector<int> dp;
public:
    void dfs(vector<int> &arr,int i,int d,int n){
        if(dp[i]!=-1){
            return ;
        }
        dp[i]=1;
        for(int w=1;w<=d&&i-w>=0&&arr[i]>arr[i-w];w++){
                dfs(arr,i-w,d,n);//记忆化搜索
                dp[i]=max(dp[i-w]+1,dp[i]);
        }
        for(int w=1;w<=d&&i+w<n&&arr[i]>arr[i+w];w++){
                dfs(arr,i+w,d,n); //记忆化搜索
                dp[i]=max(dp[i],dp[i+w]+1);
        }
    }

    int maxJumps(vector<int>& arr, int d) {
        int n=arr.size();
        dp.resize(n, -1);
        for(int i=0;i<n;i++){
            dfs(arr,i,d,n);
        }
        return *max_element(dp.begin(),dp.end());
    }
};

上面代码有三个小技巧：

1. vector的resize()函数可以批量为vector分配空间和初始值
2. max_element()函数可以返回dp.begin(),dp.end()之间的最大元素的迭代器。
3. 函数传值的时候使用引用，不仅可以在函数中对形参进行修改，也可以减少传参的开销（像这题中如果使用值得传递的话，那么就会运行超时）。

---

题目及解析来源：https://leetcode-cn.com/problems/jump-game-v/solution/tiao-yue-you-xi-v-by-leetcode-solution/