M-P模型

1. M-P模型（阈值加和模型）

M-P模型实际上是模拟人脑中单个神经元结构

生物神经元细胞如图所示:

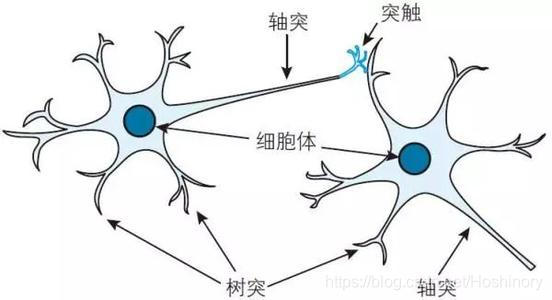
M-P模型结构如图所示:

对比生物神经元结构与M-P模型，有如下对应关系:

1	2	3	4	5	6	7	8
神经元结构	第$i$个输入神经元	第$j$个接收神经元	第$i$神经元输入到第$j$个神经元的信号	权重（连接强度）	阈值	总的膜电位	第$j$个神经元的信号输出
M-P模型	$i$	$j$	$x_{ij}$	${\omega }_{ij}$	${\theta }_j$	${\sum }_{i=1}^m{x}_{ij}{\omega }_{ij}-{\theta }_j$	$y_j=f({\sum }_{i=1}^m{x}_{ij}{\omega }_{ij}-{\theta }_j)$

生物神经元接受来自多个不同树突的电信号输入（电信号有兴奋和抑制的区别），通过神经元细胞整合后，由轴突输出。
对于M-P模型：$x_{ij}$表示第$j$个神经元接受来自第$i$个神经元的输入信号大小，${\theta }_j$表示第$j$个神经元的阈值，${\omega }_{ij}$表示连接的强弱，如果将总的膜电位加和就有${\sum }_{i=1}^m{x}_{ij}{\omega }_{ij}-{\theta }_j$，通过激活函数$f(\cdot )$，就能得到神经元$j$的输出$y_j$。
激活函数选取需要注意的性质：
非线性：当激活函数为非线性的时候，可以证明两层的神经网络可以逼近任意复杂的函数。
连续可微：由于神经网络的训练是基于梯度的优化方法，因此要求激活函数连续可微。
范围：当激活函数的取值有限时，特征的表示受有限权重的影响更显著，依仗梯度的方法会更加稳定；反之，特征的表示会则显著影响大部分权重，训练效率会更高，因此采用较小的Learning-rate就能达到目的。
单调性：如果激活函数在原点附近恒有$f(x)=x$即$f^{{}^{\prime }}(0)=1$，且$f^{{}^{\prime }}(x)$在0点连续，则使用小的随机值初始化权值就能高效地训练神经网络；反之，则需要谨慎选取初始化权值。
下面介绍几种常用的激活函数$f(\cdot )$：
（1）Binary Step函数
$$f(x)=\{\begin{array}{ll}1,& ifx\ge 0\\ 0,& ifx<0\end{array}$$
其优点是简单实用，可用于而分类问题，但是由于$f^{{}^{\prime }}(x)=0,forallx\in R$均成立，因此无法用于依仗梯度的逆向传播机制。
（2）线性函数
$$f(x)={\mathbf{\omega }}^{T}x+b,x\in R$$
优点是激活输出值与输入成正比，但由于其梯度$f^{{}^{\prime }}(x)=\mathbf{\omega }$，与$x$无关，因此无论神经网络有多少层，其输出都只是一个线性变换而且无法减少误差，因此同样也不能用于逆向传播网络中。
（3）$Sigmoid$函数
$$f(x)=\frac{1}{1+e^{-x}},x\in R$$
其优点是非线性，处处连续可微，值域$f(x)\in (0,1)$，且$f^{{}^{\prime }}(x)=f(x)(1-f(x))$，缺点是计算耗时，容易出现梯度消失问题，${\lim }_{x\to \pm \infty }{f}^{{}^{\prime }}(x)\to 0$，$\max f^{{}^{\prime }}(x)=0.25$，根据链式法则，逆向传过来的梯度至少会缩小到原来的$\frac{1}{4}$，层数越多梯度会越趋近于0，而且函数输出并不是Zero-Centered, 因为$f(x)>0forallx\in R$。

（4）$tanh$函数
$$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}},x\in R$$
具有$Sigmoid$函数的优点，$f(x)\in (-1,1)$，其$f^{{}^{\prime }}(x)=1-f^2(x)$，与$Sigmoid$函数缺点相似，${\lim }_{x\to \pm \infty }{f}^{{}^{\prime }}(x)\to 0$，因此也会出现梯度消失问题。

（5）$ReLU$函数
$$f(x)=\max (0,x),x\in R$$
不会出现梯度消失问题，运算速度快，收敛性远高于$Sigmoid$和$tanh$函数，但是输出不是Zero-Centered，而且某些神经元可能永远不会被激活，导致相应的参数永远不被更新，主要是Learning-rate过高，梯度更新过快导致的。