栈混洗概念、甄别（栈的应用一）

原创已于 2022-12-07 10:31:10 修改 · 2.2k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #数据结构

于 2022-09-28 16:38:55 首次发布

数据结构总结专栏收录该内容

2 篇文章

订阅专栏

本文介绍了栈混洗的概念，即通过特定操作将栈A中的元素转移到栈B中形成不同排序。栈混洗的计数表明，对于特定序列，存在某些排序是不可能的，如312模式。甄别栈混洗的方法包括不理想的O(n^3)枚举法，改进后的O(n^2)方法，以及高效的O(n)模拟法。文中还提及了一个用于验证栈序列的力扣习题和UVA在线判题系统的题目。

//最近听邓俊辉老师的课学数据结构，在这里对学到的知识做一些比较详细易懂的整理、梳理。

栈混洗 stack shuffle/stack permutation

概念：将栈A的顶元素弹出并压入栈S，或将栈S的顶元素弹出并压入栈B中，经过一系列的操作后，A中元素全部转入B中，则称之为A的一个栈混洗。这里标记尖括号<：栈顶，方括号 ] ：栈底，两个栈的弹出与压入次序不一样由此产生了在B栈的不同排序方式。

栈混洗的计数:

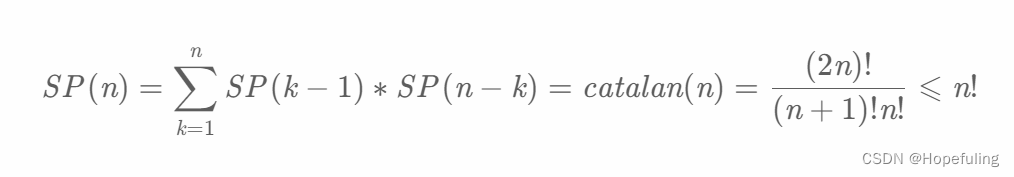
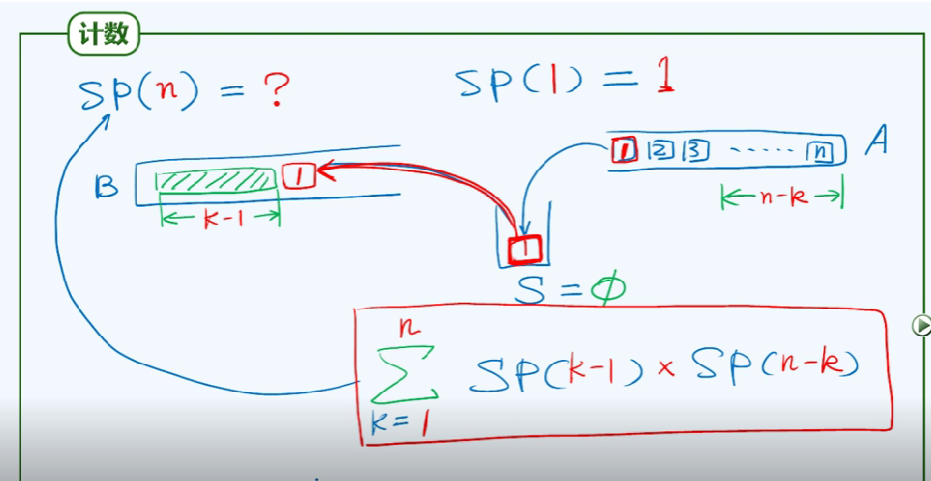
例如A:1 2 3的混洗结果可能有 123，132，213，231，321，不可能出现312 (原因如下图右上角）

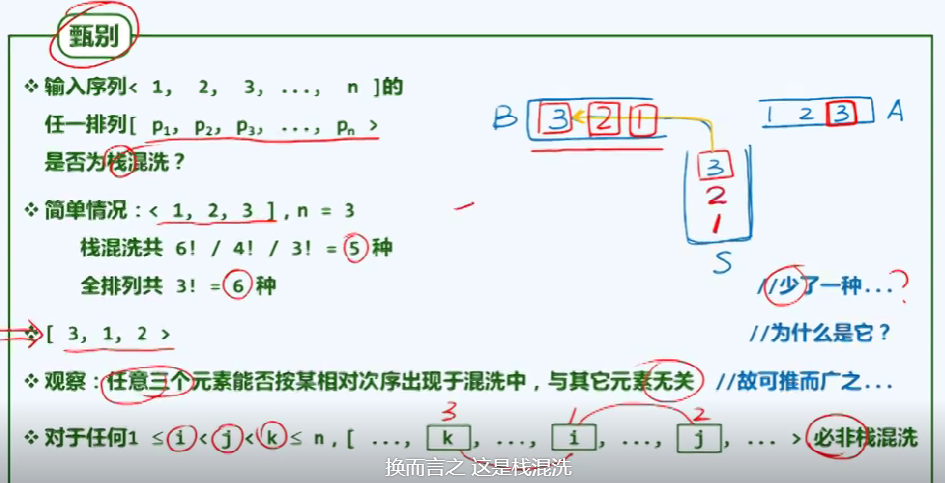
经观察，任意三个元素出现的排序方式与其他元素无关，如果出现了 k i j 的排序方式，必定不是栈混洗的结果——充要条件

如果不出现312 的模式（ j+1,i,j ）那必然是栈混洗的结果,312模式称之为禁形。

栈混洗的甄别

甄别方法有三种思路：

不断枚举i,j,k的组合复杂度 O（n^3），时间复杂度上不理想，因此不考虑。 // 这仅适用于每个元素依次递增的序列。
优化一下第一种，变成对于任意的i<j , 不含模式[ ..., j+1 , i , j....> ，但是复杂度 O（n^2）。还不能满意。
对栈混洗进行模拟。建立三个栈。如果任何一个元素匹配失败即不是栈混洗。这个复杂度仅为O（n）。

模拟一次栈混洗来解决，即每次S.pop()之前检测S是否已空，或需要弹出的元素在S中却不是顶元素，该方法用到了贪心思想。

#pragma once
#include <stack>
using namespace std;

template <typename T>
bool stackPermutation(stack<T> a, stack<T> b) // b为待检测栈
{
    stack<T> temp; // temp栈存放待检测栈b的逆序序列
    stack<T> s;    // s栈用来模拟a栈的弹出

    //把b栈倒序存放进temp栈
    while (b.size())
    {
        temp.push(b.top());
        b.pop();
    }

    //模拟栈混洗过程
    while (a.size())
    {
        s.push(a.top()); //每次弹出a的一个元素
        a.pop();

        if (s.top() == temp.top())  //判断s顶部元素是否与temp顶部元素匹配
        { 
            s.pop();
            temp.pop(); //若匹配则同时弹出，若不匹配则返回while循环，继续弹出a的元素
            while (s.size() && s.top() == temp.top()) //继续比对s中剩下的元素，匹配则弹出
            { 
                s.pop();
                temp.pop();
            }
        }//endif
    }//endwhile
    return s.empty(); //若s为空则代表栈清洗结束
}

“stackPermutation()函数的逻辑是先将待测试栈B一个个弹出到一个临时栈temp中，此时temp的栈顶就是原来B的栈底，这样就可以比较容易的来模拟一次栈混洗（因为标准库的栈容器没有下标运算符，只能出此下策），接下来以A非空为判断标准，一次一个的将元素弹出并压入S中，然后把temp的栈顶元素与刚压入S的元素（刚压入嘛，肯定是栈顶）相比较，如果相同，temp与S同时弹出这个相同的元素，接下来如果S是非空，则说明接下来S的每个元素与temp的元素相同且一一对应，所以接下来以S非空为判断标准，比较一次，弹出一次，一旦有不相等，则说明待测试栈不是给定栈的栈混洗，返回false，还有一种十分特殊的情况，如果B的栈底元素（也就是temp的栈顶元素）在A中根本就没有，即使A全部弹出，也不会触发循环里面的return false，所以，最后要用S是否为空作为判断依据返回。”

bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
        stack<int>temp;
        int n=pushed.size();
        for(int i=0,j=0;i<n;i++){
            temp.emplace(pushed[i]);
            while(!temp.empty()&&temp.top()==popped[j]){
                temp.pop();
                j++;
            }
        }//endfor
        return temp.empty();//若为空则结束，代表栈清洗成功
    }

习题：【深基15.习9】验证栈序列 - 洛谷

力扣 946. 验证栈序列

列车调度(Train)Rails - UVA 514 - Virtual Judge 解答： UVA - 514 Rails (栈混洗，贪心)_Viatorz的博客-优快云博客_栈混洗贪心算法

L2-032 彩虹瓶 http://t.csdn.cn/8c2tH

友情链接：

编程基础 - 栈的应用 - 混洗(Stack Shuffling)_沙沙的兔子的博客-优快云博客

【c++数据结构】栈混洗的甄别算法_Amirstan的博客-优快云博客

栈混洗的甄别_开车小王子的博客-优快云博客_栈混洗判断