leetcode N 皇后

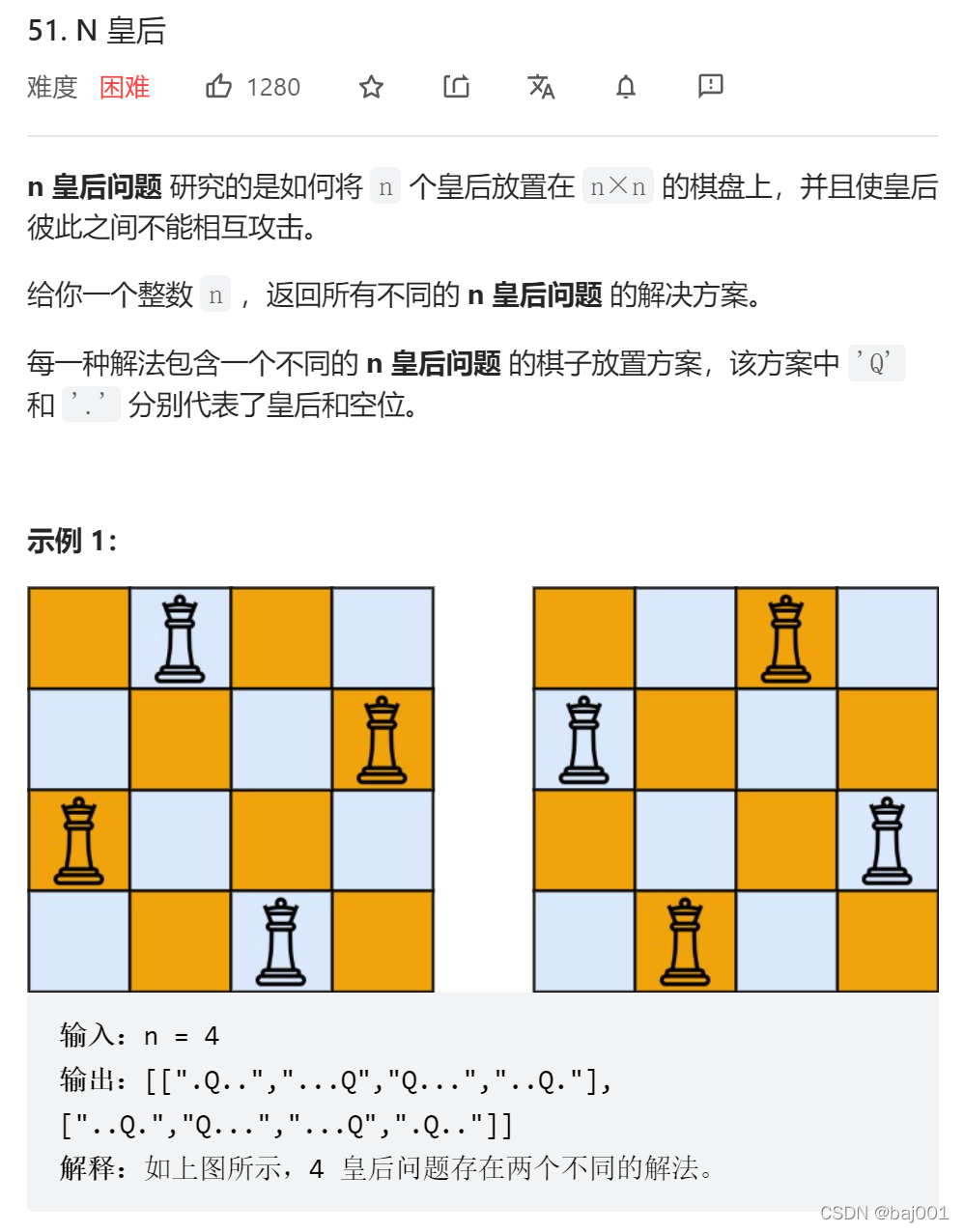
原题链接

1. 棋盘放置问题
2. 定义了回溯函数backTrack、输出字符数组函数Array2List、判断是否是有效位置函数isValid
3. 在判断是否有效位置的时候，依次判断：当前列是否包含Q，左上角和右上角对角线位置是否包含Q
4. 在回溯函数中，当该位置有效的时候，将该位置 置为Q，然后回溯进入下一行，回溯完成后，执行撤销：即将该位置置为 ‘.’号
5. 在回溯的for循环中，不断循环查找的是，每一列的位置，即选择当前行的哪一列符合条件
6. 回溯的终止条件是，当行数和皇后的个数n相同的时候，将棋盘通过Array2List函数记录后保存到res中
7. 二刷：主函数调用递归函数，递归函数调用组建结果函数Array2List，调用判断当前位置是否有效函数isValid
8. 在递归函数中，当满足条件的row出现的时候，就会调用Array2List函数将当前的chessboard 保存到res中
9. 递归函数的for循环内，若当前位置满足要求，则将此位置设置为Q，结束后撤销
10. 在构建结果的函数中，使用String.copyValueOf()函数构建结果集
11. 在最后的判断是否有效函数中，只需要判断 列、左上角、右上角，是否有Q即可**，在for循环中，不停的判断数组中的[ i ][ j ] 位置是否为Q**
12. 注意在判断是否满足条件的函数中，边界条件是包括等号的，多看看边界条件是怎么写的

class Solution {
    List<List<String>> res = new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char[][] chessboard = new char[n][n];
        for(char[] c : chessboard){
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        return res;
    }
    public void backTrack(int n, int row, char[][] chessboard){
        //截止条件
        if(row == n){
            res.add(Array2List(chessboard));
            return;
        }
        for(int col = 0; col < n; col++){
            if(isValid(row, col, n, chessboard)){
                chessboard[row][col] = 'Q';
                backTrack(n, row + 1, chessboard);
                chessboard[row][col] = '.';
            }
        }
    }
    public List Array2List(char[][] chessboard){
        List<String> list = new ArrayList<>();
        for(char[] c : chessboard){
            list.add(String.copyValueOf(c));
        }
        return list;
    }
    public boolean isValid(int row, int col, int n, char[][] chessboard){
        //判断列
        for(int i = 0; i < row; i++){
            if(chessboard[i][col] == 'Q') return false;
        }
        //判断左上角对角线是否有Q
        for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--){
            if(chessboard[i][j] == 'Q') return false;
        }
        for(int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--,j++){
            if(chessboard[i][j] == 'Q') return false;
        }
        return true;
    }
}







class Solution {
    List<List<String>> res = new ArrayList<>();

    public List<List<String>> solveNQueens(int n) {
        //主函数中定义一个棋盘，使用增强for循环，将每个位置都添加上.号
        char[][] chessboard = new char[n][n];
        for (char[] c : chessboard) {
            Arrays.fill(c, '.');
        }
        backTrack(n, 0, chessboard);
        return res;
    }

    //如下是回溯函数
    public void backTrack(int n, int row, char[][] chessboard) {
        //首先是截止条件：当行数和皇后的个数相等的时候，则说明已经到达了叶子结点，则将这一种结果加入到res中
        if (row == n) {
            res.add(Array2List(chessboard));
            return;
        }
    //使用for循环 的列表选择其中的一列，用于放置皇后
        for (int col = 0;col < n; ++col) {
            if (isValid (row, col, n, chessboard)) {
                chessboard[row][col] = 'Q';
                //当上一行选择好了位置后，来到下一行，进行选择下一行的某一列
                backTrack(n, row+1, chessboard);
                //回溯结束后，进行撤销：将该位置重新设定为.号
                chessboard[row][col] = '.';
            }
        }

    }
    //使用Array2List来记录摆放皇后的位置,使用copyValueOf将字符数组生成字符串
    public List Array2List(char[][] chessboard) {
        List<String> list = new ArrayList<>();

        for (char[] c : chessboard) {
            //copyValueOf方法：字符数组生成字符串
            list.add(String.copyValueOf(c));
        }
        return list;
    }

    //如下是检测是否有效位置的函数，给定了当前的行row和列，依次检测每一行的同一列是否有Q
    public boolean isValid(int row, int col, int n, char[][] chessboard) {
        // 检查列
        for (int i=0; i<row; ++i) { // 相当于剪枝
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }

        // 检查45度对角线，找到对应位置的行和列，然后行和列每次都减去1，即为原位置的左上角的对角线是否有Q
        for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }

        // 检查135度对角线 与左上角相似，这里是检测右上角
        for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }
}