二叉树的前序遍历、中序遍历、后序遍历---java递归非递归实现

• 本文基本参考https://blog.youkuaiyun.com/jssongwei/article/details/50790253，只供自己理解实现，侵删

• 前序遍历

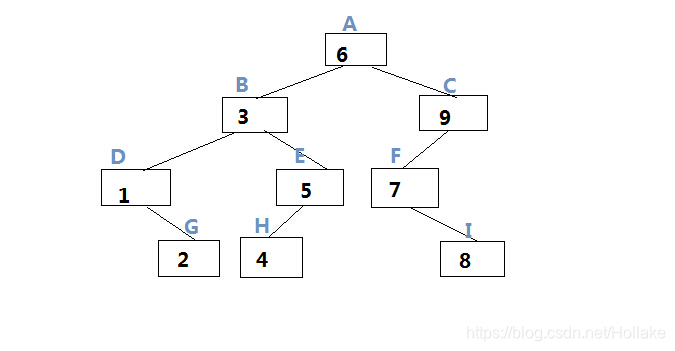
首先访问根节点，再遍历左树，再遍历右树，注意。在遍历左、右子树时，也按照先访问根节点，再遍历左树，再遍历右树。例如下图前序遍历结果为：631254978

• 中序遍历

首先遍历左子树，再访问根节点，再遍历右子树。在遍历左、右子树时，仍然先遍历左子树，再访问根结点，最后遍历右子树。例如下图中序遍历结果为：123456789

• 后序遍历

首先遍历左子树，然后遍历右子树，最后访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。例如下图后序遍历结果为：214538796

 代码实现，直接可以进行测试

• 定义二叉树数据结构：

package tree;

/**
 * Created by Administrator on 2019\4\15 0015.
 */
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;
    public TreeNode(int val){
        this.val = val;
    }

    public int getVal() {
        return val;
    }

    public void setVal(int val) {
        this.val = val;
    }

    public TreeNode getLeft() {
        return left;
    }

    public void setLeft(TreeNode left) {
        this.left = left;
    }

    public TreeNode getRight() {
        return right;
    }

    public void setRight(TreeNode right) {
        this.right = right;
    }
}

• 二叉树递归非递归实现

package tree;

import java.util.Stack;

/**
 * Created by Administrator on 2019\4\15 0015.
 */
public class MyTreeNode {
    public static void main(String[] args) {
//      二叉树初始化
        TreeNode root = MyTreeNode.init();
        System.out.println("前序遍历");
        preOrder(root);
        System.out.println();
        System.out.println("中序遍历");
        inOrder(root);
        System.out.println();
        System.out.println("后序遍历");
        postOrder(root);
        System.out.println();
        System.out.println("非递归前序遍历");
        normalPreOrder(root);
        System.out.println();
        System.out.println("非递归中序遍历");
        normalInOrder(root);
        System.out.println();
        System.out.println("非递归后序遍历");
        normalPostOrder(root);

    }



    public static void printNode(TreeNode treeNode){
        System.out.print(treeNode.getVal());
    }

    /**
     * 前序遍历
     * @param root:根节点
     */
    public static void preOrder(TreeNode root){
        printNode(root);
        if (root.getLeft() != null){
            preOrder(root.getLeft());
        }
        if (root.getRight() != null){
            preOrder(root.getRight());
        }
    }
    /**
     * 非递归前序遍历
     * @param root:根节点
     */
    public static void normalPreOrder(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        while (node != null || stack.size()>0){
            if (node != null) {
                printNode(node);
                stack.push(node);
                node = node.getLeft();
            } else {
                node = stack.pop();
                node = node.getRight();
            }
        }
    }


    /**
     * 中序遍历
     * @param root:根节点
     */
    public static void inOrder(TreeNode root){
        if (root.getLeft() != null){
            inOrder(root.getLeft());
        }
        printNode(root);
        if (root.getRight() != null){
            inOrder(root.getRight());
        }
    }

    /**
     * 非递归中序遍历
     * @param root:根节点
     */
    public static void normalInOrder(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
        TreeNode node = root;
        while (node != null || stack.size() > 0) {
            if (node != null) {
                stack.push(node);
                node = node.getLeft();
            } else {
                node = stack.pop();
                printNode(node);
                node = node.getRight();
            }
        }

    }

    /**
     * 后序遍历
     * @param root:根节点
     */
    public static void postOrder(TreeNode root) {
        if (root.getLeft() != null){
            postOrder(root.getLeft());
        }
        if (root.getRight() != null) {
            postOrder(root.getRight());
        }
        printNode(root);
    }

    /**
     * 非递归后序遍历
     * @param root:根节点
     */
    public static void normalPostOrder(TreeNode root){
        Stack<TreeNode> stack = new Stack<>();
        //构造一个中间栈来存储逆后续遍历的结果
        Stack<TreeNode> out = new Stack<>();
        TreeNode node = root;
        while (node != null || stack.size() > 0) {
            if (node != null) {
                stack.push(node);
                out.push(node);
                node = node.getRight();
            } else {
                node = stack.pop();
                node = node.getLeft();
            }
        }
        while (out.size() > 0) {
            printNode(out.pop());
        }
    }


    public static TreeNode init(){
        TreeNode A = new TreeNode(6);
        TreeNode B = new TreeNode(3);
        TreeNode C = new TreeNode(9);
        TreeNode D = new TreeNode(1);
        TreeNode E = new TreeNode(5);
        TreeNode F = new TreeNode(7);
        TreeNode G = new TreeNode(2);
        TreeNode H = new TreeNode(4);
        TreeNode I = new TreeNode(8);
        A.left = B;
        B.left = D;
        B.right = E;
        D.right = G;
        E.left = H;
        A.right = C;
        C.left = F;
        F.right = I;
        return A;
    }

}

• 输出结果

前序遍历
631254978
中序遍历
123456789
后序遍历
214538796
非递归前序遍历
631254978
非递归中序遍历
123456789
非递归后序遍历
214538796