题目练习--数组

       在上文《数组与字符串》学习了一些理论和做了一些练习题后 再开一篇文章用来记录这部分的题型

1 两栋颜色不同且距离最远的房子

 两栋颜色不同且距离最远的房子https://leetcode.cn/problems/two-furthest-houses-with-different-colors/https://leetcode.cn/problems/two-furthest-houses-with-different-colors/https://leetcode.cn/problems/two-furthest-houses-with-different-colors/https://leetcode.cn/problems/two-furthest-houses-with-different-colors/https://leetcode.cn/problems/two-furthest-houses-with-different-colors/https://leetcode.cn/problems/two-furthest-houses-with-different-colors/

街上有 n 栋房子整齐地排成一列，每栋房子都粉刷上了漂亮的颜色。给你一个下标从 0 开始且长度为 n 的整数数组 colors ，其中 colors[i] 表示第  i 栋房子的颜色。

返回 两栋 颜色 不同 房子之间的 最大 距离。

第 i 栋房子和第 j 栋房子之间的距离是 abs(i - j) ，其中 abs(x) 是 x 的绝对值。

int max(int a,int b){return a>b?a:b;}

int maxDistance(int* colors, int colorsSize) {
    
    int max_length = 0;

    for(int i = 0;i < colorsSize;i++){
        for(int j = i;j >= 0;j--){
            if(colors[j] != colors[i]){
                max_length = max(max_length,abs(i - j));
            }
        }
    }

    return max_length;
}

---

2 质数的最大距离

质数的最大距离https://leetcode.cn/problems/maximum-prime-difference/https://leetcode.cn/problems/maximum-prime-difference/https://leetcode.cn/problems/maximum-prime-difference/https://leetcode.cn/problems/maximum-prime-difference/https://leetcode.cn/problems/maximum-prime-difference/https://leetcode.cn/problems/maximum-prime-difference/

给你一个整数数组 nums。

返回两个（不一定不同的）质数在 nums 中 下标 的 最大距离。

示例 1：

输入： nums = [4,2,9,5,3]

输出： 3

解释： nums[1]、nums[3] 和 nums[4] 是质数。因此答案是 |4 - 1| = 3。

bool isPrime(int n){

   if (n <= 1) {
        return false;
    }
    for (int i = 2; i <= sqrt((double)n); i++) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

int max(int a,int b){return a>b?a:b;}

int maximumPrimeDifference(int* nums, int numsSize) {


    int left = 0;
    int right = numsSize - 1;

    while(isPrime(nums[left]) == false){
        left ++;
    }

    while(isPrime(nums[right]) == false){
       right --;
    }

    if(left == right){
        return 0;
    }

    return right - left;

}

3 构造最小位运算数组 Ⅰ

构造最小位运算数组 Ihttps://leetcode.cn/problems/construct-the-minimum-bitwise-array-i/https://leetcode.cn/problems/construct-the-minimum-bitwise-array-i/https://leetcode.cn/problems/construct-the-minimum-bitwise-array-i/https://leetcode.cn/problems/construct-the-minimum-bitwise-array-i/https://leetcode.cn/problems/construct-the-minimum-bitwise-array-i/https://leetcode.cn/problems/construct-the-minimum-bitwise-array-i/

给你一个长度为 n 的

质数

数组  nums 。你的任务是返回一个长度为  n 的数组  ans ，对于每个下标  i ，以下  条件 均成立：

• ans[i] OR (ans[i] + 1) == nums[i]

除此以外，你需要 最小化 结果数组里每一个 ans[i] 。

如果没法找到符合 条件 的 ans[i] ，那么 ans[i] = -1 。

质数 指的是一个大于 1 的自然数，且它只有 1 和自己两个因数。

 暴力破解

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* minBitwiseArray(int* nums, int numsSize, int* returnSize) {
    
    *returnSize = numsSize;
    int* ans = (int*)malloc(sizeof(int) * numsSize);
    memset(ans,-1,sizeof(int) * numsSize);

    for(int i = 0;i < numsSize;i++){
        for(int j = nums[i];j > 0;j--){
             if ((j | (j + 1)) == nums[i]) {
                ans[i] = j;
             }
        }
    }

    return ans;

}

优化解

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* minBitwiseArray(int* nums, int numsSize, int* returnSize) {
   *returnSize = numsSize;
    int* ans = (int*)malloc(sizeof(int) * numsSize);
    
    for (int i = 0; i < numsSize; ++i) {
        int num = nums[i];
        if (num == 0) {
            ans[i] = -1;
            continue;
        }
        
        int min_j = INT_MAX;
        int highest_bit = 0;
        int temp = num;
        // 计算最高位的位置
        while (temp >>= 1) {
            highest_bit++;
        }
        // 遍历每一位k
        for (int k = 0; k <= highest_bit; ++k) {
            if ((num & (1 << k)) == 0) {
                continue; // 第k位不是1，跳过
            }
            // 计算右边的位是否全为1
            int mask = (1 << k) - 1;
            if ((num & mask) == mask) {
                int j = num - (1 << k);
                if (j < min_j) {
                    min_j = j;
                }
            }
        }
        ans[i] = (min_j != INT_MAX) ? min_j : -1;
    }
    
    return ans;
}

---

4 负二进制数相加

负二进制数相加https://leetcode.cn/problems/adding-two-negabinary-numbers/https://leetcode.cn/problems/adding-two-negabinary-numbers/https://leetcode.cn/problems/adding-two-negabinary-numbers/https://leetcode.cn/problems/adding-two-negabinary-numbers/https://leetcode.cn/problems/adding-two-negabinary-numbers/https://leetcode.cn/problems/adding-two-negabinary-numbers/

给出基数为 -2 的两个数 arr1 和 arr2，返回两数相加的结果。

数字以 数组形式 给出：数组由若干 0 和 1 组成，按最高有效位到最低有效位的顺序排列。例如，arr = [1,1,0,1] 表示数字 (-2)^3 + (-2)^2 + (-2)^0 = -3。数组形式 中的数字 arr 也同样不含前导零：即 arr == [0] 或 arr[0] == 1。

返回相同表示形式的 arr1 和 arr2 相加的结果。两数的表示形式为：不含前导零、由若干 0 和 1 组成的数组。

// 用于反转数组元素顺序的辅助函数
void reverse(int *arr, int len) {
    for (int i = 0; i < len / 2; i++) {
        int temp = arr[i];
        arr[i] = arr[len - 1 - i];
        arr[len - 1 - i] = temp;
    }
}

// 主函数，实现两个基数为 -2 的数组相加
int* addNegabinary(int* arr1, int arr1Size, int* arr2, int arr2Size, int* returnSize) {
    // 从最低位开始处理，因此先反转数组
    reverse(arr1, arr1Size);
    reverse(arr2, arr2Size);

    int carry = 0;
    int maxSize = (arr1Size > arr2Size) ? arr1Size : arr2Size;
    int *result = (int *)calloc(maxSize + 2, sizeof(int));
    *returnSize = 0;

    for (int i = 0; i < maxSize || carry; i++) {
        int digit = carry;
        if (i < arr1Size) digit += arr1[i];
        if (i < arr2Size) digit += arr2[i];

        result[(*returnSize)++] = digit & 1;
        carry = -(digit >> 1);
    }

    // 移除前导零
    while (*returnSize > 1 && result[*returnSize - 1] == 0) {
        (*returnSize)--;
    }

    // 最后再反转结果数组以恢复正常顺序
    reverse(result, *returnSize);
    return result;
}

---

5 统计一致字符串的数目

统计一致字符串的数目https://leetcode.cn/problems/count-the-number-of-consistent-strings/https://leetcode.cn/problems/count-the-number-of-consistent-strings/https://leetcode.cn/problems/count-the-number-of-consistent-strings/https://leetcode.cn/problems/count-the-number-of-consistent-strings/https://leetcode.cn/problems/count-the-number-of-consistent-strings/

给你一个由不同字符组成的字符串 allowed 和一个字符串数组 words 。如果一个字符串的每一个字符都在 allowed 中，就称这个字符串是 一致字符串 。

请你返回 words 数组中 一致字符串 的数目。

 暴力破解

int countConsistentStrings(char* allowed, char** words, int wordsSize) {
    
    int number = 0;

    int length = strlen(allowed);

    for(int i = 0;i < wordsSize; i++){
        int word_length = strlen(words[i]);
        int flag = 0;
       for(int j = 0;j < word_length;j++){

            for(int k = 0;k < length;k++){
                if(words[i][j] != allowed[k]){
                     continue;
                }else{
                    flag ++;
                }
            }

        }

        if(flag == word_length){
            number ++;
        }

    }

    return number;
}

优化解

优化了allowed数组的查找使用了 类哈希的一种方式 节省了一次遍历

int countConsistentStrings(char* allowed, char** words, int wordsSize) {
    int allowedChars[26] = {0};
    // 标记允许的字符
    for (int i = 0; allowed[i]; ++i) {
        allowedChars[allowed[i] - 'a'] = 1;
    }
    
    int count = 0;
    for (int i = 0; i < wordsSize; ++i) {
        char* word = words[i];
        int valid = 1;
        // 检查单词中的每个字符
        for (int j = 0; word[j]; ++j) {
            if (!allowedChars[word[j] - 'a']) {
                valid = 0;
                break;
            }
        }
        count += valid;
    }
    return count;
}

---

6 地图中的最高点

地图中的最高点https://leetcode.cn/problems/map-of-highest-peak/https://leetcode.cn/problems/map-of-highest-peak/https://leetcode.cn/problems/map-of-highest-peak/https://leetcode.cn/problems/map-of-highest-peak/https://leetcode.cn/problems/map-of-highest-peak/

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

• 如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
• 如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。

你需要按照如下规则给每个单元格安排高度：

• 每个格子的高度都必须是非负的。
• 如果一个格子是 水域 ，那么它的高度必须为 0 。
• 任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

这里是使用了广度搜索的算法（关于搜索的部分需要再继续学习）

typedef struct {
    int row;
    int col;
} Point;

int** highestPeak(int** isWater, int isWaterSize, int* isWaterColSize, int* returnSize, int** returnColumnSizes) {
    int m = isWaterSize;
    int n = isWaterColSize[0];
    *returnSize = m;
    *returnColumnSizes = (int*)malloc(m * sizeof(int));
    
    for (int i = 0; i < m; i++) {
        (*returnColumnSizes)[i] = n;
    }
    
    int** height = (int**)malloc(m * sizeof(int*));
    for (int i = 0; i < m; i++) {
        height[i] = (int*)malloc(n * sizeof(int));
    }
    
    // 队列相关初始化
    Point* queue = (Point*)malloc(m * n * sizeof(Point));
    int front = 0, rear = 0;
    
    // 初始化height矩阵并将所有水域加入队列
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (isWater[i][j] == 1) {
                height[i][j] = 0;
                queue[rear].row = i;
                queue[rear].col = j;
                rear++;
            } else {
                height[i][j] = -1;
            }
        }
    }
    
    // 四个方向的偏移量：上下左右
    int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
    while (front < rear) {
        Point curr = queue[front];
        front++;
        for (int d = 0; d < 4; d++) {
            int ni = curr.row + dirs[d][0];
            int nj = curr.col + dirs[d][1];
            if (ni >= 0 && ni < m && nj >= 0 && nj < n && height[ni][nj] == -1) {
                height[ni][nj] = height[curr.row][curr.col] + 1;
                queue[rear].row = ni;
                queue[rear].col = nj;
                rear++;
            }
        }
    }
    
    free(queue);
    return height;
}

---

7 二分查找

二分查找https://leetcode.cn/problems/binary-search/https://leetcode.cn/problems/binary-search/https://leetcode.cn/problems/binary-search/https://leetcode.cn/problems/binary-search/https://leetcode.cn/problems/binary-search/

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

int search(int* nums, int numsSize, int target) {
    
    int left = 0;
    int right = numsSize - 1;
    int mid = -1;

    if(numsSize == 1){return nums[0] == target?0:-1;}

    while(left <= right){
        mid = (left + right) / 2;
        if(nums[mid] == target){
            return mid;
        }else if(nums[mid] > target){
            right = mid - 1;
        }else{
            left = mid + 1;
        }
    }

    return -1;
}

---

8 写字符串需要的行数

写字符串需要的行数https://leetcode.cn/problems/number-of-lines-to-write-string/https://leetcode.cn/problems/number-of-lines-to-write-string/https://leetcode.cn/problems/number-of-lines-to-write-string/https://leetcode.cn/problems/number-of-lines-to-write-string/https://leetcode.cn/problems/number-of-lines-to-write-string/

我们要把给定的字符串 S 从左到右写到每一行上，每一行的最大宽度为100个单位，如果我们在写某个字母的时候会使这行超过了100 个单位，那么我们应该把这个字母写到下一行。我们给定了一个数组 widths ，这个数组 widths[0] 代表 'a' 需要的单位， widths[1] 代表 'b' 需要的单位，...， widths[25] 代表 'z' 需要的单位。

现在回答两个问题：至少多少行能放下S，以及最后一行使用的宽度是多少个单位？将你的答案作为长度为2的整数列表返回。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* numberOfLines(int* widths, int widthsSize, char* s, int* returnSize) {
    
    int number = 0;
    int col = 1;
    *returnSize = 2;

    int length = strlen(s);
    for(int i = 0;i < length;i++){

        if(number + widths[s[i] - 'a'] <= 100){
            number += widths[s[i] - 'a'];
        }else{
            col ++;
            number =  widths[s[i] - 'a'];
        }
    
    }

    int* ans = (int*)malloc(sizeof(int) * 2);

    ans[0] = col;
    ans[1] = number;

    return ans;
}

---

9 网格图中机器人回家的最小代价

网格图中机器人回家的最小代价https://leetcode.cn/problems/minimum-cost-homecoming-of-a-robot-in-a-grid/https://leetcode.cn/problems/minimum-cost-homecoming-of-a-robot-in-a-grid/https://leetcode.cn/problems/minimum-cost-homecoming-of-a-robot-in-a-grid/https://leetcode.cn/problems/minimum-cost-homecoming-of-a-robot-in-a-grid/https://leetcode.cn/problems/minimum-cost-homecoming-of-a-robot-in-a-grid/

给你一个 m x n 的网格图，其中 (0, 0) 是最左上角的格子，(m - 1, n - 1) 是最右下角的格子。给你一个整数数组 startPos ，startPos = [startrow, startcol] 表示 初始 有一个 机器人 在格子 (startrow, startcol) 处。同时给你一个整数数组 homePos ，homePos = [homerow, homecol] 表示机器人的 家 在格子 (homerow, homecol) 处。

机器人需要回家。每一步它可以往四个方向移动：上，下，左，右，同时机器人不能移出边界。每一步移动都有一定代价。再给你两个下标从 0 开始的额整数数组：长度为 m 的数组 rowCosts  和长度为 n 的数组 colCosts 。

• 如果机器人往 上 或者往 下 移动到第 r 行 的格子，那么代价为 rowCosts[r] 。
• 如果机器人往 左 或者往 右 移动到第 c 列 的格子，那么代价为 colCosts[c] 。

请你返回机器人回家需要的 最小总代价 。

这道题在解答时 考虑使用div方向数组来寻找最短路径（没有考虑路径重复）进入死循环（后续修改通过但是性能不如直接逼近）没有想到直接从起始位置循环逼近目标位置 

int min(int a,int b){return a<b?a:b;}

int minCost(int* startPos, int startPosSize, int* homePos, int homePosSize, int* rowCosts, int rowCostsSize, int* colCosts, int colCostsSize) {
    int curRow = startPos[0];
    int curCol = startPos[1];
    int targetRow = homePos[0];
    int targetCol = homePos[1];
    int totalCost = 0;

    // 表示四个方向的移动：下、上、右、左
    int div[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};

    while (curRow != targetRow || curCol != targetCol) {
        int minCost = 1e9; // 初始化为一个较大的值
        int nextRow = curRow;
        int nextCol = curCol;

        // 遍历四个方向
        for (int i = 0; i < 4; i++) {
            int newRow = curRow + div[i][0];
            int newCol = curCol + div[i][1];

            // 检查新位置是否合法
            if (newRow >= 0 && newRow < rowCostsSize && newCol >= 0 && newCol < colCostsSize) {
                int cost;
                if (div[i][0] != 0) {
                    cost = rowCosts[newRow];
                } else {
                    cost = colCosts[newCol];
                }

                // 判断新位置是否更接近目标位置
                int distBefore = abs(curRow - targetRow) + abs(curCol - targetCol);
                int distAfter = abs(newRow - targetRow) + abs(newCol - targetCol);
                if (distAfter < distBefore && cost < minCost) {
                    minCost = cost;
                    nextRow = newRow;
                    nextCol = newCol;
                }
            }
        }

        // 更新当前位置和总花费
        curRow = nextRow;
        curCol = nextCol;
        totalCost += minCost;
    }

    return totalCost;
}

直接循环逼近目标位置

int min(int a,int b){return a<b?a:b;}

int minCost(int* startPos, int startPosSize, int* homePos, int homePosSize, int* rowCosts, int rowCostsSize, int* colCosts, int colCostsSize) {
    int startRow = startPos[0];
    int startCol = startPos[1];
    int homeRow = homePos[0];
    int homeCol = homePos[1];
    int cost = 0;

    // 计算垂直方向的移动花费
    if (startRow < homeRow) {
        for (int i = startRow + 1; i <= homeRow; i++) {
            cost += rowCosts[i];
        }
    } else if (startRow > homeRow) {
        for (int i = startRow - 1; i >= homeRow; i--) {
            cost += rowCosts[i];
        }
    }

    // 计算水平方向的移动花费
    if (startCol < homeCol) {
        for (int i = startCol + 1; i <= homeCol; i++) {
            cost += colCosts[i];
        }
    } else if (startCol > homeCol) {
        for (int i = startCol - 1; i >= homeCol; i--) {
            cost += colCosts[i];
        }
    }

    return cost;
}

---

10 消灭怪物的最大数量

消灭怪物的最大数量https://leetcode.cn/problems/eliminate-maximum-number-of-monsters/https://leetcode.cn/problems/eliminate-maximum-number-of-monsters/https://leetcode.cn/problems/eliminate-maximum-number-of-monsters/https://leetcode.cn/problems/eliminate-maximum-number-of-monsters/https://leetcode.cn/problems/eliminate-maximum-number-of-monsters/

你正在玩一款电子游戏，在游戏中你需要保护城市免受怪物侵袭。给定一个 下标从 0 开始 且大小为 n 的整数数组 dist ，其中 dist[i] 是第 i 个怪物与城市的 初始距离（单位：千米）。

怪物以 恒定 的速度走向城市。每个怪物的速度都以一个长度为 n 的整数数组 speed 表示，其中 speed[i] 是第 i 个怪物的速度（单位：千米/分）。

你有一种武器，一旦充满电，就可以消灭 一个 怪物。但是，武器需要 一分钟 才能充电。武器在游戏开始时是充满电的状态，怪物从 第 0 分钟 时开始移动。

一旦任一怪物到达城市，你就输掉了这场游戏。如果某个怪物 恰好 在某一分钟开始时到达城市（距离表示为0），这也会被视为 输掉 游戏，在你可以使用武器之前，游戏就会结束。

返回在你输掉游戏前可以消灭的怪物的 最大 数量。如果你可以在所有怪物到达城市前将它们全部消灭，返回  n 。

按照时间顺序消灭

// 比较函数，用于 qsort 进行递增排序
int compare(const void *a, const void *b) {
    return (*(int *)a - *(int *)b);
}

int eliminateMaximum(int* dist, int distSize, int* speed, int speedSize) {
    int *arrivalTimes = (int *)malloc(distSize * sizeof(int));
    if (arrivalTimes == NULL) {
        return -1; // 内存分配失败
    }

    // 计算每个怪物到达的时间
    for (int i = 0; i < distSize; i++) {
        arrivalTimes[i] = (dist[i] + speed[i] - 1) / speed[i];
    }

    // 对到达时间进行递增排序
    qsort(arrivalTimes, distSize, sizeof(int), compare);

    // 按时间顺序处理怪物
    for (int i = 0; i < distSize; i++) {
        if (arrivalTimes[i] <= i) {
            free(arrivalTimes);
            return i;
        }
    }

    free(arrivalTimes);
    return distSize;
}

最开始时想着模拟这样一个过程 即怪物一次一次移动 然后判断消灭（就是按照距离顺序消灭）但是这样存在逻辑问题 就是说该怪物距离近但是速度慢 先把它消灭了就会产生问题 所以应该按照怪物到达的时间进行排序 然后进行消灭和判断。后续再优化就是优化排序部分（可以在插入的就绩进行排序）

---

11 统计是给定字符串前缀的字符串数目

统计是给定字符串前缀的字符串数目https://leetcode.cn/problems/count-prefixes-of-a-given-string/https://leetcode.cn/problems/count-prefixes-of-a-given-string/https://leetcode.cn/problems/count-prefixes-of-a-given-string/https://leetcode.cn/problems/count-prefixes-of-a-given-string/https://leetcode.cn/problems/count-prefixes-of-a-given-string/

给你一个字符串数组 words 和一个字符串 s ，其中 words[i] 和 s 只包含 小写英文字母 。

请你返回 words 中是字符串 s 前缀 的 字符串数目 。

一个字符串的 前缀 是出现在字符串开头的子字符串。子字符串 是一个字符串中的连续一段字符序列。

 暴力破解

int countPrefixes(char** words, int wordsSize, char* s) {
    
    int number = 0;
    int length = strlen(s);

    for(int i = 0;i < wordsSize;i++){

        int p = 0;
        int word_length = strlen(words[i]);

        if(word_length > length){continue;}

        for(int j = 0;j < word_length;j++){

            if(words[i][j] == s[j]){
                p ++;
            }else{
                break;
            }

        }

        if(p == word_length){number ++;}

    }

    return number;

}

优化解

这里是忘记了c语言中有自己的字符串的比较函数strcmp 可以优化一下性能

int countPrefixes(char** words, int wordsSize, char* s) {
    int count = 0;
    int sLength = strlen(s);

    for (int i = 0; i < wordsSize; i++) {
        int wordLength = strlen(words[i]);
        // 若单词长度大于 s 的长度，肯定不是前缀，跳过
        if (wordLength > sLength) {
            continue;
        }
        // 使用 strncmp 比较单词和 s 的前 wordLength 个字符
        if (strncmp(words[i], s, wordLength) == 0) {
            count++;
        }
    }

    return count;
}

---

12 连续数组

连续数组https://leetcode.cn/problems/A1NYOS/https://leetcode.cn/problems/A1NYOS/https://leetcode.cn/problems/A1NYOS/https://leetcode.cn/problems/A1NYOS/https://leetcode.cn/problems/A1NYOS/

给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组，并返回该子数组的长度。

 使用哈希表来存储前缀和

int max(int a,int b){return a>b?a:b;}

int findMaxLength(int* nums, int numsSize) {
    // 为了存储前缀和及其对应的索引，需要一个哈希表，这里简单用数组模拟
    int max_length = 0;
    int *hash = (int *)malloc((2 * numsSize + 1) * sizeof(int));
    for (int i = 0; i < 2 * numsSize + 1; i++) {
        hash[i] = -2;  // 初始化为 -2 表示未访问过
    }
    hash[numsSize] = -1;  // 前缀和为 0 的起始索引设为 -1

    int sum = 0;
    for (int i = 0; i < numsSize; i++) {
        // 将 0 视为 -1，方便计算前缀和
        sum += (nums[i] == 0) ? -1 : 1;
        if (hash[sum + numsSize] == -2) {
            // 如果该前缀和第一次出现，记录其索引
            hash[sum + numsSize] = i;
        } else {
            // 如果该前缀和已经出现过，计算当前子数组的长度
            max_length = max(max_length, i - hash[sum + numsSize]);
        }
    }

    free(hash);
    return max_length;
}

---

13 寻找峰值 Ⅱ

寻找峰值 IIhttps://leetcode.cn/problems/find-a-peak-element-ii/https://leetcode.cn/problems/find-a-peak-element-ii/https://leetcode.cn/problems/find-a-peak-element-ii/https://leetcode.cn/problems/find-a-peak-element-ii/https://leetcode.cn/problems/find-a-peak-element-ii/

一个 2D 网格中的 峰值 是指那些 严格大于 其相邻格子(上、下、左、右)的元素。

给你一个 从 0 开始编号 的 m x n 矩阵 mat ，其中任意两个相邻格子的值都 不相同 。找出 任意一个 峰值 mat[i][j] 并 返回其位置 [i,j] 。

你可以假设整个矩阵周边环绕着一圈值为 -1 的格子。

要求必须写出时间复杂度为 O(m log(n)) 或 O(n log(m)) 的算法

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int max(int a,int b){return a>b?a:b;}

bool man_V(int** mat, int matSize, int* matColSize,int x,int y){

    int left = (y == 0 ? -1:mat[x][y-1]);
    int right = (y == matColSize[x] - 1?-1:mat[x][y+1]);
    int up = (x == 0 ? -1:mat[x-1][y]);
    int down = (x == matSize - 1 ? -1:mat[x+1][y]);

    if(mat[x][y] > left && mat[x][y] > right && mat[x][y] > up && mat[x][y] > down){
        return true;
    }else{
        return false;
    }

}

int* findPeakGrid(int** mat, int matSize, int* matColSize, int* returnSize) {

    *returnSize = 2;
    int* ans = (int*)malloc(sizeof(int) * 2);

    int row = 0;
    int col = 0;

    int div[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
   
    while(!man_V(mat,matSize,matColSize,row,col)){


        int new_row,new_col;
        int max = mat[row][col];

        for(int i = 0;i < 4;i++){

            int drow = row + div[i][0];
            int dcol = col + div[i][1];

            if(drow >= 0 && drow < matSize && dcol >=0 && dcol < matColSize[drow]){
                if(mat[drow][dcol] > max){
                    max = mat[drow][dcol];
                    new_row = drow;
                    new_col = dcol;
                }
            } 
        }

        row = new_row;
        col = new_col;
    }

    ans[0] = row;
    ans[1] = col;
    return ans;
    
}

---

14 最后一块石头的重量 Ⅱ

最后一块石头的重量 IIhttps://leetcode.cn/problems/last-stone-weight-ii/https://leetcode.cn/problems/last-stone-weight-ii/https://leetcode.cn/problems/last-stone-weight-ii/https://leetcode.cn/problems/last-stone-weight-ii/https://leetcode.cn/problems/last-stone-weight-ii/

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

这是动态规划 0-1背包问题 这部分的思想和空间优化下的滚动数组在后续知识补充站简单介绍 

// 比较两个整数大小，返回较大值
int max(int a, int b) {
    return a > b ? a : b;
}

// 计算最后剩下石头的最小可能重量
int lastStoneWeightII(int* stones, int stonesSize) {
    int totalWeight = 0;
    // 计算所有石头的总重量
    for (int i = 0; i < stonesSize; i++) {
        totalWeight += stones[i];
    }
    int target = totalWeight / 2;

    /*将所有石头的总重量除以 2，得到目标重量 target。这里的思路是，
    要使最后剩下的石头重量最小，就需要把这堆石头尽量平均地分成两堆，
    让两堆石头重量之和的差值最小。所以我们的目标是在这些石头中选择一部分，
    使其重量之和尽可能接近 totalWeight / 2*/

    int* dp = (int*)calloc(target + 1, sizeof(int));

    /*dp[j] 表示在当前考虑的石头中，能组合出的重量不超过 j 的最大重量。*/

    // 遍历每一块石头
    for (int i = 0; i < stonesSize; i++) {
        // 从目标重量开始倒序更新 dp 数组
        for (int j = target; j >= stones[i]; j--) {
            dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
        }
    }
    // 计算最后剩下石头的最小可能重量
    int result = totalWeight - 2 * dp[target];
    free(dp);
    return result;
}

---

15 找出数组中的第K大整数

找出数组中的第 K 大整数https://leetcode.cn/problems/find-the-kth-largest-integer-in-the-array/https://leetcode.cn/problems/find-the-kth-largest-integer-in-the-array/https://leetcode.cn/problems/find-the-kth-largest-integer-in-the-array/https://leetcode.cn/problems/find-the-kth-largest-integer-in-the-array/https://leetcode.cn/problems/find-the-kth-largest-integer-in-the-array/

给你一个字符串数组 nums 和一个整数 k 。nums 中的每个字符串都表示一个不含前导零的整数。

返回 nums 中表示第 k 大整数的字符串。

注意：重复的数字在统计时会视为不同元素考虑。例如，如果 nums 是 ["1","2","2"]，那么 "2" 是最大的整数，"2" 是第二大的整数，"1" 是第三大的整数。

暴力破解（错误）

最开始的想法是转换字符串为整型 然后再转换回字符串 但是由于long long型使用还会有溢出问题

// 比较函数，用于 qsort 递减排序
int compare(const void *a, const void *b) {
    return (*(long long *)b - *(long long *)a); // 递减排序
}

// 将字符串转换为长整型
long long stringToLongLong(char *str) {
    return strtoll(str, NULL, 10); // 使用 strtoll 将字符串转换为 long long
}

// 将长整型转换为字符串
char* longLongToString(long long number) {
    // 计算数字的位数
    int n = 0;
    long long temp = number;
    if (temp == 0) n = 1; // 处理 0 的情况
    while (temp != 0) {
        n++;
        temp /= 10;
    }

    // 分配内存（包括字符串结束符 '\0'）
    char *ans = (char *)malloc(sizeof(char) * (n + 1));
    if (ans == NULL) return NULL; // 内存分配失败

    // 将数字转换为字符串
    sprintf(ans, "%lld", number);
    return ans;
}

// 主函数
char* kthLargestNumber(char** nums, int numsSize, int k) {
    // 将字符串数组转换为长整型数组
    long long *ans = (long long *)malloc(sizeof(long long) * numsSize);
    if (ans == NULL) return NULL; // 内存分配失败

    for (int i = 0; i < numsSize; i++) {
        ans[i] = stringToLongLong(nums[i]);
    }

    // 对长整型数组进行递减排序
    qsort(ans, numsSize, sizeof(long long), compare);

    // 将第 k 大的数转换为字符串
    char *result = longLongToString(ans[k - 1]);

    // 释放内存
    free(ans);

    return result;
}

优化解

使用比较字符串长度和数组的字典序来进行比较排序

// 比较函数，用于 qsort 递减排序
int compare(const void *a, const void *b) {
    const char *str1 = *(const char **)a;
    const char *str2 = *(const char **)b;
    int len1 = strlen(str1);
    int len2 = strlen(str2);

    // 长度不同，长度长的数字大
    if (len1 != len2) {
        return len2 - len1;
    }
    // 长度相同，按字典序比较
    return strcmp(str2, str1);
}

char* kthLargestNumber(char** nums, int numsSize, int k) {
    // 直接对字符串数组进行排序
    qsort(nums, numsSize, sizeof(char *), compare);

    // 返回第 k 大的字符串
    return nums[k - 1];
}

---

16 找出叠涂元素

找出叠涂元素https://leetcode.cn/problems/first-completely-painted-row-or-column/https://leetcode.cn/problems/first-completely-painted-row-or-column/https://leetcode.cn/problems/first-completely-painted-row-or-column/https://leetcode.cn/problems/first-completely-painted-row-or-column/https://leetcode.cn/problems/first-completely-painted-row-or-column/

给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数 矩阵 mat 。arr 和 mat 都包含范围 [1，m * n] 内的 所有 整数。

从下标 0 开始遍历 arr 中的每个下标 i ，并将包含整数 arr[i] 的 mat 单元格涂色。

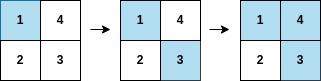
请你找出 arr 中第一个使得 mat 的某一行或某一列都被涂色的元素，并返回其下标 i 。

示例 1：

输入：arr = [1,3,4,2], mat = [[1,4],[2,3]]
输出：2
解释：遍历如上图所示，arr[2] 在矩阵中的第一行或第二列上都被涂色。

 暴力破解

int min(int a, int b) {
    return a < b ? a : b;
}

int firstCompleteIndex(int* arr, int arrSize, int** mat, int matSize, int* matColSize) {
    int m = matSize;          // 矩阵行数
    int n = matColSize[0];    // 矩阵列数

    // 哈希表：记录每个值在矩阵中的行和列位置
    int *rowMap = (int *)malloc(sizeof(int) * (m * n + 1));
    int *colMap = (int *)malloc(sizeof(int) * (m * n + 1));

    // 初始化哈希表
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            rowMap[mat[i][j]] = i; // 记录值 mat[i][j] 所在的行
            colMap[mat[i][j]] = j; // 记录值 mat[i][j] 所在的列
        }
    }

    // 统计每行和每列被覆盖的次数
    int *rowCount = (int *)calloc(m, sizeof(int));
    int *colCount = (int *)calloc(n, sizeof(int));

    // 遍历 arr
    for (int i = 0; i < arrSize; i++) {
        int val = arr[i];
        int row = rowMap[val]; // 获取当前值所在的行
        int col = colMap[val]; // 获取当前值所在的列

        // 更新行和列的覆盖次数
        rowCount[row]++;
        colCount[col]++;

        // 检查是否某一行或某一列被完全覆盖
        if (rowCount[row] == n || colCount[col] == m) {
            // 释放内存
            free(rowMap);
            free(colMap);
            free(rowCount);
            free(colCount);
            return i; // 返回当前索引
        }
    }

    // 释放内存
    free(rowMap);
    free(colMap);
    free(rowCount);
    free(colCount);

    return -1; // 如果没有找到，返回 -1
}

优化解（力扣官方题解）

int firstCompleteIndex(int* arr, int arrSize, int** mat, int matSize, int* matColSize){
    int n = matSize, m = matColSize[0];
    int mp[m * n + 1][2];
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
            mp[mat[i][j]][0] = i;
            mp[mat[i][j]][1] = j;
        }
    }
    int rowCnt[n], colCnt[m];
    memset(rowCnt, 0, sizeof(int) * n);
    memset(colCnt, 0, sizeof(int) * m);
    for (int i = 0; i < arrSize; i++) {
        int *v = mp[arr[i]];
        rowCnt[v[0]]++;
        if (rowCnt[v[0]] == m) {
            return i;
        }
        colCnt[v[1]]++;
        if (colCnt[v[1]] == n) {
            return i;
        }
    }
    return -1;
}

---

17 只出现一次的数字

只出现一次的数字https://leetcode.cn/problems/single-number/https://leetcode.cn/problems/single-number/https://leetcode.cn/problems/single-number/https://leetcode.cn/problems/single-number/https://leetcode.cn/problems/single-number/

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

暴力破解

使用哈希来查找只出现一次的值

class Solution {
    public int singleNumber(int[] nums) {
    HashMap<Integer,Integer> map = new HashMap();

    for(int i = 0;i < nums.length;i++){
        if(map.get(nums[i]) == null){
            map.put(nums[i],-1);
        }else{
            map.put(nums[i],1);
        }
    }

    for(int i = 0;i < nums.length;i++){
       if(map.get(nums[i]) == -1){
         return nums[i];
       }
    }
    return -1;
  }
}

 优化解（异或运算）

class Solution {
    public int singleNumber(int[] nums) {
        int result = 0;
        for (int num : nums) {
            result ^= num;
        }
        return result;
    }
}

---

18 将数组清空

将数组清空https://leetcode.cn/problems/make-array-empty/https://leetcode.cn/problems/make-array-empty/https://leetcode.cn/problems/make-array-empty/https://leetcode.cn/problems/make-array-empty/

给你一个包含若干 互不相同 整数的数组 nums ，你需要执行以下操作 直到数组为空 ：

• 如果数组中第一个元素是当前数组中的 最小值 ，则删除它。
• 否则，将第一个元素移动到数组的 末尾 。

请你返回需要多少个操作使 nums 为空。

// 定义结构体，包含元素的值和其在原数组中的索引
typedef struct {
    long long val;
    int index;
} Element;

// 比较函数，用于 qsort 排序
int compare(const void *a, const void *b) {
    const Element elemA = *(const Element *)a;
    const Element elemB = *(const Element *)b;
    return (elemA.val < elemB.val) ? -1 : (elemA.val > elemB.val);
}

long long countOperationsToEmptyArray(int* nums, int numsSize) {
    // 处理边界情况
    if (numsSize == 0) return 0;
    if (numsSize == 1) return 1;

    // 创建结构体数组
    Element *elements = (Element *)malloc(numsSize * sizeof(Element));
    if (elements == NULL) {
        return -1; // 内存分配失败
    }

    // 初始化结构体数组
    for (int i = 0; i < numsSize; i++) {
        elements[i].val = nums[i];
        elements[i].index = i;
    }

    // 对结构体数组按元素值排序
    qsort(elements, numsSize, sizeof(Element), compare);

    long long operations = numsSize; // 初始操作次数为数组长度
    for (int i = 1; i < numsSize; i++) {
        if (elements[i].index < elements[i - 1].index) {
            // 如果当前元素的索引小于前一个元素的索引，说明需要额外的旋转操作
            operations += (long long)(numsSize - i);
        }
    }

    // 释放内存
    free(elements);

    return operations;
}

---

19 绝对差不超过限制的最长连续子数组 *

绝对差不超过限制的最长连续子数组https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/

给你一个整数数组 nums ，和一个表示限制的整数 limit，请你返回最长连续子数组的长度，该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。

如果不存在满足条件的子数组，则返回 0 。

// 找到满足条件的最长连续子数组的长度
int longestSubarray(int* nums, int numsSize, int limit) {
    // 用于存储单调队列的数组
    int maxQueue[100000];
    int minQueue[100000];
    // 单调队列的首尾指针
    int maxFront = 0, maxRear = 0;
    int minFront = 0, minRear = 0;
    int left = 0, right = 0;
    int maxLength = 0;

    while (right < numsSize) {
        // 维护最大值单调队列（单调递减）
        while (maxRear > maxFront && nums[right] > maxQueue[maxRear - 1]) {
            maxRear--;
        }
        maxQueue[maxRear++] = nums[right];

        // 维护最小值单调队列（单调递增）
        while (minRear > minFront && nums[right] < minQueue[minRear - 1]) {
            minRear--;
        }
        minQueue[minRear++] = nums[right];

        // 当窗口内最大元素和最小元素差值大于 limit 时，移动左指针
        while (maxQueue[maxFront] - minQueue[minFront] > limit) {
            if (nums[left] == maxQueue[maxFront]) {
                maxFront++;
            }
            if (nums[left] == minQueue[minFront]) {
                minFront++;
            }
            left++;
        }

        // 更新最长子数组的长度
        if (right - left + 1 > maxLength) {
            maxLength = right - left + 1;
        }
        right++;
    }

    return maxLength;
}

---

 20 计数质数

计数质数https://leetcode.cn/problems/count-primes/https://leetcode.cn/problems/count-primes/https://leetcode.cn/problems/count-primes/https://leetcode.cn/problems/count-primes/

给定整数 n ，返回 所有小于非负整数 n 的质数的数量 。

 暴力破解（超出时限）

 暴力法在面对数字比较大的情况下 大量判断 效率太低

bool fun(int n) {

    if (n < 2) return false;

    if (n == 2) return true;

    if (n % 2 == 0) return false;

    // 只检查奇数因子
    for (int i = 3; i <= sqrt(n); i += 2) {
        if (n % i == 0) {
            return false;
        }
    }
    return true;
}

int countPrimes(int n) {
    
    int number = 0;
    for(int i = 2;i < n;i++){
        if(fun(i)){
            number ++;
        }
    }

    return number;
}

优化解（埃拉托斯特尼筛法）

这是一种找质数的方式 核心就是把使用布尔数组来记录质数 找到一个质数就将其倍数标记为非质数

// 埃拉托斯特尼筛法计算小于 n 的质数数量
int countPrimes(int n) {
    if (n <= 2) return 0;

    // 创建一个布尔数组，初始值都为 true，表示都是质数
    bool *isPrime = (bool *)malloc(n * sizeof(bool));
    for (int i = 0; i < n; i++) {
        isPrime[i] = true;
    }
    // 0 和 1 不是质数
    isPrime[0] = isPrime[1] = false;

    // 埃拉托斯特尼筛法
    for (int i = 2; i * i < n; i++) {
        if (isPrime[i]) {
            // 将 i 的倍数标记为非质数
            for (int j = i * i; j < n; j += i) {
                isPrime[j] = false;
            }
        }
    }

    // 统计质数的数量
    int count = 0;
    for (int i = 2; i < n; i++) {
        if (isPrime[i]) {
            count++;
        }
    }

    // 释放动态分配的内存
    free(isPrime);

    return count;
}

---

21 统计匹配检索规则的物品数量

统计匹配检索规则的物品数量https://leetcode.cn/problems/count-items-matching-a-rule/https://leetcode.cn/problems/count-items-matching-a-rule/https://leetcode.cn/problems/count-items-matching-a-rule/https://leetcode.cn/problems/count-items-matching-a-rule/

给你一个数组 items ，其中 items[i] = [typei, colori, namei] ，描述第 i 件物品的类型、颜色以及名称。

另给你一条由两个字符串 ruleKey 和 ruleValue 表示的检索规则。

如果第 i 件物品能满足下述条件之一，则认为该物品与给定的检索规则 匹配 ：

• ruleKey == "type" 且 ruleValue == typei 。
• ruleKey == "color" 且 ruleValue == colori 。
• ruleKey == "name" 且 ruleValue == namei 。

统计并返回 匹配检索规则的物品数量 。

这道题是简单的 只是刚开始以为是一个三重指针去循环嵌套做了 后面发现是一个多行三列数组 只需要按列索引编列即可

int countMatches(char*** items, int itemsSize, int* itemsColSize, char* ruleKey, char* ruleValue) {
    int number = 0;
    int colIndex;

    // 根据 ruleKey 确定要比较的列索引
    if (strcmp(ruleKey, "type") == 0) {
        colIndex = 0;
    } else if (strcmp(ruleKey, "color") == 0) {
        colIndex = 1;
    } else {
        colIndex = 2;
    }

    // 遍历每一行，比较对应列的字符串
    for (int i = 0; i < itemsSize; i++) {
        if (strcmp(items[i][colIndex], ruleValue) == 0) {
            number++;
        }
    }

    return number;
}

---

22 修车的最少时间

修车的最少时间https://leetcode.cn/problems/minimum-time-to-repair-cars/https://leetcode.cn/problems/minimum-time-to-repair-cars/https://leetcode.cn/problems/minimum-time-to-repair-cars/https://leetcode.cn/problems/minimum-time-to-repair-cars/

给你一个整数数组 ranks ，表示一些机械工的 能力值 。ranksi 是第 i 位机械工的能力值。能力值为 r 的机械工可以在 r * n2 分钟内修好 n 辆车。

同时给你一个整数 cars ，表示总共需要修理的汽车数目。

请你返回修理所有汽车 最少 需要多少时间。

注意：所有机械工可以同时修理汽车。

// 函数用于检查在给定时间内是否能修理完所有汽车
int canRepairCars(int *ranks, int ranksSize, int cars, long long time) {
    long long totalCars = 0;
    for (int i = 0; i < ranksSize; i++) {
        // 计算在给定时间内每个机械工能修理的汽车数量
        totalCars += (long long)sqrt((double)time / ranks[i]);
    }
    return totalCars >= cars;
}

// 函数用于计算修理所有汽车最少需要的时间
long long repairCars(int *ranks, int ranksSize, int cars) {
    long long left = 0;
    // 计算二分查找的右边界，假设让能力最强的机械工（ranks 中的最小值）修理所有汽车所需的时间
    int minRank = ranks[0];
    for (int i = 1; i < ranksSize; i++) {
        if (ranks[i] < minRank) {
            minRank = ranks[i];
        }
    }
    long long right = (long long)minRank * cars * cars;

    while (left < right) {
        long long mid = left + (right - left) / 2;
        if (canRepairCars(ranks, ranksSize, cars, mid)) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

---

23 半径为K的子数组平均值

半径为 k 的子数组平均值https://leetcode.cn/problems/k-radius-subarray-averages/https://leetcode.cn/problems/k-radius-subarray-averages/https://leetcode.cn/problems/k-radius-subarray-averages/https://leetcode.cn/problems/k-radius-subarray-averages/

给你一个下标从 0 开始的数组 nums ，数组中有 n 个整数，另给你一个整数 k 。

半径为 k 的子数组平均值 是指：nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值，即下标在 i - k 和 i + k 范围（含 i - k 和 i + k）内所有元素的平均值。如果在下标 i 前或后不足 k 个元素，那么 半径为 k 的子数组平均值 是 -1 。

构建并返回一个长度为 n 的数组 avgs ，其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。

x 个元素的 平均值 是 x 个元素相加之和除以 x ，此时使用截断式 整数除法 ，即需要去掉结果的小数部分。

• 例如，四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75，截断后得到 2 。

前缀和解法

使用前缀和来计算 i-k 到 i+k 之间的总和 简化一部分计算 但是不是最优解 然后要注意边界和特殊情况（本题 k == 0 和 k > numsSize/2 的两个情况 返回错误）

int* getAverages(int* nums, int numsSize, int k, int* returnSize) {
    
    int* ans = (int*)malloc(sizeof(int) * numsSize);
    *returnSize = numsSize;

    // 初始化结果数组为 -1
    for (int i = 0; i < numsSize; i++) {
        ans[i] = -1;
    }

    // 如果 k 为 0，直接将 nums 数组元素复制到结果数组
    if (k == 0) {
        for (int i = 0; i < numsSize; i++) {
            ans[i] = nums[i];
        }
        return ans;
    }

    // 计算前缀和
    long long* sum = (long long*)malloc(sizeof(long long) * numsSize);
    sum[0] = nums[0];
    for (int i = 1; i < numsSize; i++) {
        sum[i] = sum[i - 1] + nums[i];
    }

    // 计算平均值
    for (int i = k; i < numsSize - k; i++) {
        long long rangeSum;
        if (i - k - 1 >= 0) {
            rangeSum = sum[i + k] - sum[i - k - 1];
        } else {
            rangeSum = sum[i + k];
        }
        ans[i] = (int)(rangeSum / (2 * k + 1));
    }

    free(sum);
    return ans;
}

 滑动窗口解法

这种解法直观上更好理解 时间复杂度为O(n)，其中n 是数组 nums 的长度。代码只对数组进行了一次遍历，每次遍历的操作都是常数时间的，因此时间复杂度为线性。

int* getAverages(int* nums, int numsSize, int k, int* returnSize) {
    int* ans = (int*)malloc(numsSize * sizeof(int));
    *returnSize = numsSize;

    // 初始化结果数组为 -1
    for (int i = 0; i < numsSize; i++) {
        ans[i] = -1;
    }

    // 如果窗口大小大于数组长度，直接返回结果数组
    if (2 * k + 1 > numsSize) {
        return ans;
    }

    long long windowSum = 0;
    // 初始化窗口
    for (int i = 0; i < 2 * k + 1; i++) {
        windowSum += nums[i];
    }
    ans[k] = (int)(windowSum / (2 * k + 1));

    // 滑动窗口计算平均值
    for (int i = 2 * k + 1; i < numsSize; i++) {
        // 移除窗口最左边的元素
        windowSum -= nums[i - (2 * k + 1)];
        // 添加窗口最右边的新元素
        windowSum += nums[i];
        ans[i - k] = (int)(windowSum / (2 * k + 1));
    }

    return ans;
}

---

24 所有球里面不同颜色的数目

所有球里面不同颜色的数目https://leetcode.cn/problems/find-the-number-of-distinct-colors-among-the-balls/https://leetcode.cn/problems/find-the-number-of-distinct-colors-among-the-balls/https://leetcode.cn/problems/find-the-number-of-distinct-colors-among-the-balls/https://leetcode.cn/problems/find-the-number-of-distinct-colors-among-the-balls/

给你一个整数 limit 和一个大小为 n x 2 的二维数组 queries 。

总共有 limit + 1 个球，每个球的编号为 [0, limit] 中一个 互不相同 的数字。一开始，所有球都没有颜色。queries 中每次操作的格式为 [x, y] ，你需要将球 x 染上颜色 y 。每次操作之后，你需要求出所有球中 不同 颜色的数目。

请你返回一个长度为 n 的数组 result ，其中 result[i] 是第 i 次操作以后不同颜色的数目。

注意 ，没有染色的球不算作一种颜色。

 暴力破解（超时限）

使用两个数组 一个来存储球的颜色 一个来存储球的数量 大体思路上正确的 只是在存储上 数量太大 数组要么是堆溢出 要么是超时

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* queryResults(int limit, int** queries, int queriesSize, int* queriesColSize, int* returnSize) {
    
    int* result = (int*)malloc(sizeof(int) * queriesSize);
    *returnSize = queriesSize;

    int number = 0;

    int balls[limit+1];
    long long  colors[1000];
    memset(balls,0,sizeof(int) * (limit + 1));
    memset(colors,0,sizeof(long long) * (100));

    for(int i = 0;i < queriesSize;i++){

        int ball = queries[i][0];
        int color = queries[i][1];

        // 处理球之前的颜色
        if (balls[ball] != 0) {
            int oldColor = balls[ball];
            colors[oldColor]--;
            if (colors[oldColor] == 0) {
                number--;
            }
        }
        // 更新球的颜色
        balls[ball] = color;
        // 处理新颜色
        if (colors[color] == 0) {
            number++;
        }
        colors[color]++;

        result[i] = number;
    }


    return result;
}

优化解（哈希表）

算法的思路是相似的 只是使用哈希表的形式来存储数据 效率更高

// 定义哈希表节点结构体
typedef struct HashNode {
    int key;  // 颜色编号
    long long value;  // 该颜色的球的数量
    struct HashNode* next;  // 指向下一个节点的指针
} HashNode;

// 定义哈希表结构体
typedef struct {
    HashNode** table;  // 哈希表数组
    int size;  // 哈希表大小
} HashTable;

// 创建哈希表
HashTable* createHashTable(int size) {
    HashTable* hashTable = (HashTable*)malloc(sizeof(HashTable));
    hashTable->size = size;
    hashTable->table = (HashNode**)calloc(size, sizeof(HashNode*));
    return hashTable;
}

// 哈希函数
int hash(int key, int size) {
    return key % size;
}

// 查找键对应的值
long long get(HashTable* hashTable, int key) {
    int index = hash(key, hashTable->size);
    HashNode* node = hashTable->table[index];
    while (node != NULL) {
        if (node->key == key) {
            return node->value;
        }
        node = node->next;
    }
    return 0;
}

// 插入或更新键值对
void insertOrUpdate(HashTable* hashTable, int key, long long value) {
    int index = hash(key, hashTable->size);
    HashNode* node = hashTable->table[index];
    while (node != NULL) {
        if (node->key == key) {
            node->value = value;
            return;
        }
        node = node->next;
    }
    HashNode* newNode = (HashNode*)malloc(sizeof(HashNode));
    newNode->key = key;
    newNode->value = value;
    newNode->next = hashTable->table[index];
    hashTable->table[index] = newNode;
}

// 释放哈希表内存
void freeHashTable(HashTable* hashTable) {
    for (int i = 0; i < hashTable->size; i++) {
        HashNode* node = hashTable->table[i];
        while (node != NULL) {
            HashNode* temp = node;
            node = node->next;
            free(temp);
        }
    }
    free(hashTable->table);
    free(hashTable);
}

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* queryResults(int limit, int** queries, int queriesSize, int* queriesColSize, int* returnSize) {
    if (queries == NULL || queriesSize == 0) {
        *returnSize = 0;
        return NULL;
    }

    int* result = (int*)malloc(sizeof(int) * queriesSize);
    *returnSize = queriesSize;

    int number = 0;
    int* balls = (int*)calloc(limit + 1, sizeof(int));
    HashTable* colors = createHashTable(1000);  // 哈希表大小可根据实际情况调整

    for (int i = 0; i < queriesSize; i++) {
        int ball = queries[i][0];
        int color = queries[i][1];

        if (ball < 0 || ball > limit) {
            continue;  // 忽略无效的球编号
        }

        // 处理球之前的颜色
        if (balls[ball] != 0) {
            int oldColor = balls[ball];
            long long oldCount = get(colors, oldColor);
            insertOrUpdate(colors, oldColor, oldCount - 1);
            if (oldCount - 1 == 0) {
                number--;
            }
        }

        // 更新球的颜色
        balls[ball] = color;

        // 处理新颜色
        long long newCount = get(colors, color);
        if (newCount == 0) {
            number++;
        }
        insertOrUpdate(colors, color, newCount + 1);

        result[i] = number;
    }

    free(balls);
    freeHashTable(colors);
    return result;
}

---

25 零矩阵

零矩阵https://leetcode.cn/problems/zero-matrix-lcci/https://leetcode.cn/problems/zero-matrix-lcci/https://leetcode.cn/problems/zero-matrix-lcci/https://leetcode.cn/problems/zero-matrix-lcci/

编写一种算法，若M × N矩阵中某个元素为0，则将其所在的行与列清零。

 暴力破解

 这道题不知道为什么暴力也能过 效率还可以

void setZeroes(int** matrix, int matrixSize, int* matrixColSize) {
    
    int row[matrixSize];
    int col[matrixColSize[0]];

    memset(row,0,sizeof(int) * matrixSize);
    memset(col,0,sizeof(int) * matrixColSize[0]);

    for(int i = 0;i < matrixSize;i++){
        for(int j = 0;j < matrixColSize[0];j++){
            if(matrix[i][j] == 0){
                row[i] ++;
                col[j] ++;
            }
        }
    }

    for(int i = 0;i < matrixSize;i++){
        if(row[i] != 0){
            for(int j = 0;j < matrixColSize[0];j++){
                matrix[i][j] = 0;
            }
        }
    }

    for(int i = 0;i < matrixColSize[0];i++){
        if(col[i] != 0){
            for(int j = 0;j < matrixSize;j++){
                matrix[j][i] = 0;
            }
        }
    }
}

 优化（优化不大）

void setZeroes(int** matrix, int matrixSize, int* matrixColSize) {
    // 标记第一行和第一列是否原本就有 0
    int firstRowHasZero = 0;
    int firstColHasZero = 0;

    // 检查第一行是否有 0
    for (int j = 0; j < matrixColSize[0]; j++) {
        if (matrix[0][j] == 0) {
            firstRowHasZero = 1;
            break;
        }
    }

    // 检查第一列是否有 0
    for (int i = 0; i < matrixSize; i++) {
        if (matrix[i][0] == 0) {
            firstColHasZero = 1;
            break;
        }
    }

    // 利用第一行和第一列来标记其他行和列
    for (int i = 1; i < matrixSize; i++) {
        for (int j = 1; j < matrixColSize[0]; j++) {
            if (matrix[i][j] == 0) {
                matrix[i][0] = 0;
                matrix[0][j] = 0;
            }
        }
    }

    // 根据标记将对应行和列置 0
    for (int i = 1; i < matrixSize; i++) {
        for (int j = 1; j < matrixColSize[0]; j++) {
            if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                matrix[i][j] = 0;
            }
        }
    }

    // 处理第一行
    if (firstRowHasZero) {
        for (int j = 0; j < matrixColSize[0]; j++) {
            matrix[0][j] = 0;
        }
    }

    // 处理第一列
    if (firstColHasZero) {
        for (int i = 0; i < matrixSize; i++) {
            matrix[i][0] = 0;
        }
    }
}

---

26 找出前缀异或的原始数组

找出前缀异或的原始数组https://leetcode.cn/problems/find-the-original-array-of-prefix-xor/https://leetcode.cn/problems/find-the-original-array-of-prefix-xor/https://leetcode.cn/problems/find-the-original-array-of-prefix-xor/https://leetcode.cn/problems/find-the-original-array-of-prefix-xor/

给你一个长度为 n 的 整数 数组 pref 。找出并返回满足下述条件且长度为 n 的数组 arr ：

• pref[i] = arr[0] ^ arr[1] ^ ... ^ arr[i].

注意 ^ 表示 按位异或（bitwise-xor）运算。

可以证明答案是 唯一 的。

暴力破解（异或的逆运算还是异或）

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* findArray(int* pref, int prefSize, int* returnSize) {

    // if(prefSize == 1){return pref;}
    
    *returnSize = prefSize;
    int* ans = (int*)malloc(sizeof(int)*prefSize);
    int* arr = (int*)malloc(sizeof(int)*prefSize);

    arr[0] = pref[0];
    ans[0] = pref[0];

    for(int i = 1;i < prefSize;i++){
        
        ans[i] = pref[i] ^ arr[i-1];
        arr[i] = ans[i] ^ arr[i-1];
        

    }

    return ans;
}

优化解

直接使用异或的性质 不占用额外的空间

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */

int* findArray(int* pref, int prefSize, int* returnSize) {
    int* arr = (int*)malloc(sizeof(int) * (prefSize));

    arr[0] = pref[0]; // 第一个元素直接赋值
    for (int i = 1; i < prefSize; i++) {
        arr[i] =  pref[i] ^ pref[i - 1];
    }
    *returnSize = prefSize;
    return arr;
}

---

 27 卡牌分组

卡牌分组https://leetcode.cn/problems/x-of-a-kind-in-a-deck-of-cards/https://leetcode.cn/problems/x-of-a-kind-in-a-deck-of-cards/https://leetcode.cn/problems/x-of-a-kind-in-a-deck-of-cards/https://leetcode.cn/problems/x-of-a-kind-in-a-deck-of-cards/

给定一副牌，每张牌上都写着一个整数。

此时，你需要选定一个数字 X，使我们可以将整副牌按下述规则分成 1 组或更多组：

• 每组都有 X 张牌。
• 组内所有的牌上都写着相同的整数。

仅当你可选的 X >= 2 时返回 true。

暴力破解

// 求最大公约数的函数
int gcd(int a, int b) {
    while (b != 0) {
        int temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

bool hasGroupsSizeX(int* deck, int deckSize) {
    if (deckSize < 2) {
        return false;
    }

    // 假设 deck 中的元素范围是 0 到 10000
    int count[10001] = {0};

    // 统计每个元素的出现次数
    for (int i = 0; i < deckSize; i++) {
        count[deck[i]]++;
    }

    int currentGcd = -1;
    for (int i = 0; i < 10001; i++) {
        if (count[i] > 0) {
            if (currentGcd == -1) {
                currentGcd = count[i];
            } else {
                currentGcd = gcd(currentGcd, count[i]);
            }
        }
    }

    // 如果最大公约数大于等于 2，则返回 true
    return currentGcd >= 2;
}

---

28 判断两个事件是否存在冲突

判断两个事件是否存在冲突https://leetcode.cn/problems/determine-if-two-events-have-conflict/https://leetcode.cn/problems/determine-if-two-events-have-conflict/https://leetcode.cn/problems/determine-if-two-events-have-conflict/

给你两个字符串数组 event1 和 event2 ，表示发生在同一天的两个闭区间时间段事件，其中：

• event1 = [startTime1, endTime1] 且
• event2 = [startTime2, endTime2]

事件的时间为有效的 24 小时制且按 HH:MM 格式给出。

当两个事件存在某个非空的交集时（即，某些时刻是两个事件都包含的），则认为出现 冲突 。

如果两个事件之间存在冲突，返回 true ；否则，返回 false 。

暴力破解（字符串转int来比较）

int charToTime(char* arr){

    return (arr[0] *10 + arr[1]) * 60 + (arr[3] * 10 + arr[4]);
}

bool haveConflict(char** event1, int event1Size, char** event2, int event2Size) {

    int event1Start = charToTime(event1[0]);
    int event1End = charToTime(event1[1]);

    int event2Start = charToTime(event2[0]);
    int event2End = charToTime(event2[1]);

    
    if(event1End < event2Start || (event1Start > event2Start && event2End < event1Start)){
        return false;
    }else{
        return true;
    }
}

---

29 出租车的最大盈利 *

出租车的最大盈利

你驾驶出租车行驶在一条有 n 个地点的路上。这 n 个地点从近到远编号为 1 到 n ，你想要从 1 开到 n ，通过接乘客订单盈利。你只能沿着编号递增的方向前进，不能改变方向。

乘客信息用一个下标从 0 开始的二维数组 rides 表示，其中 rides[i] = [starti, endi, tipi] 表示第 i 位乘客需要从地点 starti 前往 endi ，愿意支付 tipi 元的小费。

每一位 你选择接单的乘客 i ，你可以 盈利 endi - starti + tipi 元。你同时 最多 只能接一个订单。

给你 n 和 rides ，请你返回在最优接单方案下，你能盈利 最多 多少元。

注意：你可以在一个地点放下一位乘客，并在同一个地点接上另一位乘客。

int cmp(const void *a, const void *b) {
    int* rideA = *(int**) a;
    int* rideB = *(int**) b;
    return rideA[1] - rideB[1];
}

long long maxTaxiEarnings(int n, int** rides, int ridesSize, int* ridesColSize) {
    qsort(rides, ridesSize, sizeof(int*), cmp);
    long long* dp = calloc(n + 1, sizeof(long long));
    int i = 1, j = 0;
    dp[0] = 0;

    while (i <= n && j < ridesSize) {
        while (i <= n && i != rides[j][1]) {
            dp[i] = dp[i - 1];
            i++;
        }
        while (j < ridesSize && rides[j][1] == i) {
            dp[i] = fmaxl(dp[i], fmaxl(dp[i - 1], rides[j][1] - rides[j][0] + rides[j][2] + dp[rides[j][0]]));
            j++;
        }
        i++;
    }
    while (i <= n) {
        dp[i] = dp[i - 1];
        i++;
    }
    return dp[n];
}

---

30 回旋镖的数量

回旋镖的数量https://leetcode.cn/problems/number-of-boomerangs/https://leetcode.cn/problems/number-of-boomerangs/

给定平面上 n 对 互不相同 的点 points ，其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ，其中 i 和 j 之间的欧式距离和 i 和 k 之间的欧式距离相等（需要考虑元组的顺序）。

返回平面上所有回旋镖的数量。

#include <stdio.h>
#include <stdlib.h>

// 计算两点之间的欧几里得距离的平方
int distanceSquared(int *p1, int *p2) {
    int dx = p1[0] - p2[0];
    int dy = p1[1] - p2[1];
    return dx * dx + dy * dy;
}

// 比较函数，用于 qsort 排序
int compare(const void *a, const void *b) {
    return (*(int *)a - *(int *)b);
}

// 计算回旋镖的数量
int numberOfBoomerangs(int **points, int pointsSize, int *pointsColSize) {
    int ans = 0;

    // 遍历每个点作为回旋镖的中心点
    for (int i = 0; i < pointsSize; i++) {
        // 动态分配数组来存储到其他点的距离的平方
        int *distances = (int *)malloc((pointsSize - 1) * sizeof(int));
        if (distances == NULL) {
            return -1; // 内存分配失败
        }

        int index = 0;
        // 计算到其他点的距离的平方
        for (int j = 0; j < pointsSize; j++) {
            if (i != j) {
                distances[index++] = distanceSquared(points[i], points[j]);
            }
        }

        // 对距离的平方数组进行排序
        qsort(distances, pointsSize - 1, sizeof(int), compare);

        int count = 1;
        // 统计相同距离的点的数量
        for (int k = 1; k < pointsSize - 1; k++) {
            if (distances[k] == distances[k - 1]) {
                count++;
            } else {
                // 计算以当前距离相同的点可以组成的回旋镖数量
                ans += count * (count - 1);
                count = 1;
            }
        }
        // 处理最后一组相同距离的点
        ans += count * (count - 1);

        // 释放动态分配的内存
        free(distances);
    }

    return ans;
}

---

 知识补充站

0-1 背包问题

问题定义

场景：
给定一组物品，每个物品有重量 weight[i] 和价值 value[i]，以及一个容量为 W 的背包。要求选择若干物品装入背包，使得：

1. 总重量不超过背包容量。

2. 总价值最大。

3. 每个物品只能选或不选（不可拆分）。

---

核心思想

01背包问题的本质是在有限资源（背包容量）下做最优决策。动态规划通过分解问题为子问题，并记录子问题的解来避免重复计算。

---

解法步骤

1. 定义状态

设 dp[i][w] 表示：

• 前 i 个物品（物品编号从 1 到 i）

• 在背包容量为 w 时

• 能获得的最大价值。

2. 状态转移方程

对每个物品 i，分两种情况：

• 不选第 i 个物品：
  dp[i][w] = dp[i-1][w]（直接继承前 i-1 个物品的结果）

• 选第 i 个物品：
  dp[i][w] = dp[i-1][w - weight[i]] + value[i]
  （前提：w >= weight[i]，即背包剩余容量足够放下该物品）

最终结果：
dp[i][w] = max(不选, 选)，即取两种情况的最大值。

3. 初始化

• 当 i=0（没有物品）时，无论背包容量多大，价值均为 0。

• 当 w=0（背包容量为0）时，无法放入任何物品，价值为 0。

4. 填表顺序

• 外层循环遍历物品（i 从 1 到 n）。

• 内层循环遍历背包容量（w 从 1 到 W）。

---

空间优化（一维滚动数组）

二维数组 dp[i][w] 的空间复杂度为 O(nW)，可优化为一维数组 dp[w]，将空间复杂度降至 O(W)。
关键点：倒序遍历背包容量（从 W 到 weight[i]），避免提前更新覆盖上一轮的结果。

这里的dp[w]表示的是在背包容量为w时 背包的最大价值

优化后的状态转移方程：

for (int i = 1; i <= n; i++) {
    for (int w = W; w >= weight[i]; w--) {
        dp[w] = max(dp[w], dp[w - weight[i]] + value[i]);
    }
}

---

总结：简单题基本都能做 中等题有的只能暴力过 困难题很费力 现在完成不了 还需要练习 先我那成专题专项的练习后 后续以一周一总结 （一天完成3-5题） 算法学习真的才刚刚拉开帷幕啊

---

学习时间  2025.02.07- 02.08