强化学习(Reinforcement Learning)入门知识

强化学习(Reinforcement Learning)

概率统计知识

1. 随机变量和观测值

• 抛硬币是一个随机事件，其结果为**随机变量 X **

• 正面为1，反面为0，若第 i 次试验中为正面，则观测值 x_i=1

2. 概率密度函数

• 物理意义：随机变量在某个确定的取值点附近的可能性

  **例如：高斯分布（正态分布）**的概率密度函数如下

  

  • **μ **是均值

  • **σ **是标准差

    

  • 横轴为随机变量的取值，纵轴为概率密度

  • 曲线为高斯分布的概率密度函数p(X)，这个概率密度说明 X 在原点附近取值的概率比较大，远离原点的地方取值的概率比较小。

    **离散的概率分布: **

  • 随机变量只能取{1,3,7}这几个值，X=1时的概率为0.2，X=3的概率为0.5，X=7的概率为0.3，其它任何地方概率都为0。

• 若p是连续概率分布
  • 可以对p(X)做定积分，对所有X取值定积分结果为1
• 若p是离散概率分布
  • 可以对p(X)做加和，对所有X取值加和结果为1

3. 期望

• 连续分布：对p(x)和f(x)的乘积做定积分

• 离散分布：对p(x)和f(x)的乘积进行连加

  

4. 随机抽样

• 10个球：2红3蓝5绿，随机取一个，概率0.2红0.3蓝0.5绿，颜色为随机变量，红/蓝/绿为观测值，该过程即为**随机抽样（Random Sampling）****
• 球数未知：抽取记录颜色再放回，大量试验后，计算每个颜色出现概率（例如0.2、0.3 、0.5），也是随机抽样（Random Sampling）

强化学习相关术语

概述

1. 强化学习关注智能体与环境之间的交互
2. 强化学习目标一般是追求最大回报或实现特定目标

解释

强化学习的学习机制：学习如何从状态映射到行为以使得获取的奖励最大。代理（agent）需要不断地在环境中进行实验，通过环境给予的反馈（奖励）来不断优化状态-行为的对应关系。

强化学习最重要的两个特征：反复实验(trial and error）、延迟奖励（delayed reward）

特点

• 不存在监督，只有反馈（奖励）信号
• 反馈是延迟的（非即使）
• 智能体行为会影响后续数据

要素

基本要素：策略（policy）、奖励（reward）、价值（value）、模型（model）

策略：

1. 策略定义智能体的行为

2. 策略是从**状态（state）到行为（action）**的映射

3. 策略本身可以是具体映射或者随机分布

   policy函数 π 是一个概率密度函数：

   

   • 给定状态 s 作出动作 a 的概率密度

奖励：

1. 奖励是一个即时性的标量反馈信号

2. 奖励所表征的是某一步当中，智能体的表现如何

3. 智能体目标即为：最大化奖励

   奖励需要人为定义，某个目标的奖励根据该目标的重要程度定义其奖励大小

价值（价值函数）：

1. 价值函数是对未来奖励的预测
2. 能够评估状态的好坏
3. 价值函数的计算需要对状态之间的转移进行分析

模型（环境）：

• 不基于模型：无模型，直接对策略和价值函数进行分析
• 基于模型：存在模型对环境进行模拟
  1. 模型可以预测环境下一步的表现
  2. 其表现由预测的状态和奖励来反映

架构

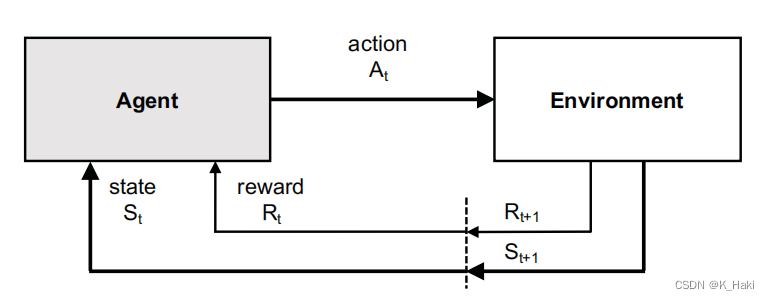
理解：

从当前状态S_t 出发，作出一个行为A_t 后，对环境产生一些影响，然后环境对Agent产生反馈R_t+1 ,进而Agent进入一个新的状态S_t+1 。

强化学习基本概念

1. Return

t 时刻的 return : U_t = R_t + R_t+1 + R_t+2 + R_t+3 + …

• 未来的不确定性很大，所以未来 R_t+1 的权重应该比 R_t 低，也就是对 R_t+1 打一个折扣，那么定义这个折扣值（折扣率）为 γ（0<γ<1）

• (折扣率) γ 是一个超参数需要自己定义，其设置对强化学习有一定的影响

  

  • 每个奖励 R_i 都和状态 S_i 和 A_i 有关，那么 U_t 就跟 t 时刻开始未来所有的状态和动作相关

    

2. 价值函数

• 用于评估当前形式如何，可以对 U_t 求期望，将得到的数记作 Q_π
• 如何求 Q_π 呢？
  • 未来的动作A和状态S都有随机性，动作A的概率密度函数是policy函数π(a|s)，状态S的概率密度函数是状态转移函数p(s’ |s,a)，利用积分及概率密度函数求其期望，则避免了考虑未来状态以及动作的随机性
  • 所以，此时 Q_π 只与当前状态 S_t 和动作 A_t 有关
  • 函数 Q_π 与policy 函数 π 有关，因为积分的时候需要用到policy函数

3. Q_π

直观意义：判断在当前状态下某个动作是好还是坏，即 Q_π 对当前状态下的所有动作进行打分

优化： Q_π 与π有关，使用不同的policy函数会得到不同的 Q_π ，如何将 π 去掉？

• 对 π 关于 Q_π 求最大化：寻找使 Q_π 最大的那个 π ，最终得到 Q * 函数，称为：最优动作价值函数（Optimal action-value function）

• 最终根据 Q * 函数的值来选择该时刻的动作 A

  

状态价值函数（State-value function）

直观意义：判断当前局势好不好

• V_π 是动作价值函数 Q_π 的期望
• 这里的期望都是根据随机变量 A 来求的，A 的概率密度函数是 π
  • 若动作离散，则将期望写成连加：把 π 和 Q 的乘积做连加（包含所有的动作）
  • 若动作连续，则将期望写成积分形式，期望等于 π 和 Q 的乘积做积分，把动作a积掉

声明一下

该篇是小白学习强化学习时做的学习笔记，参考链接如下：

参考链接1：https://blog.youkuaiyun.com/CltCj/article/details/119445005

参考链接2：https://blog.youkuaiyun.com/weixin_45560318/article/details/112981006