4.1 函数依赖
-
函数依赖

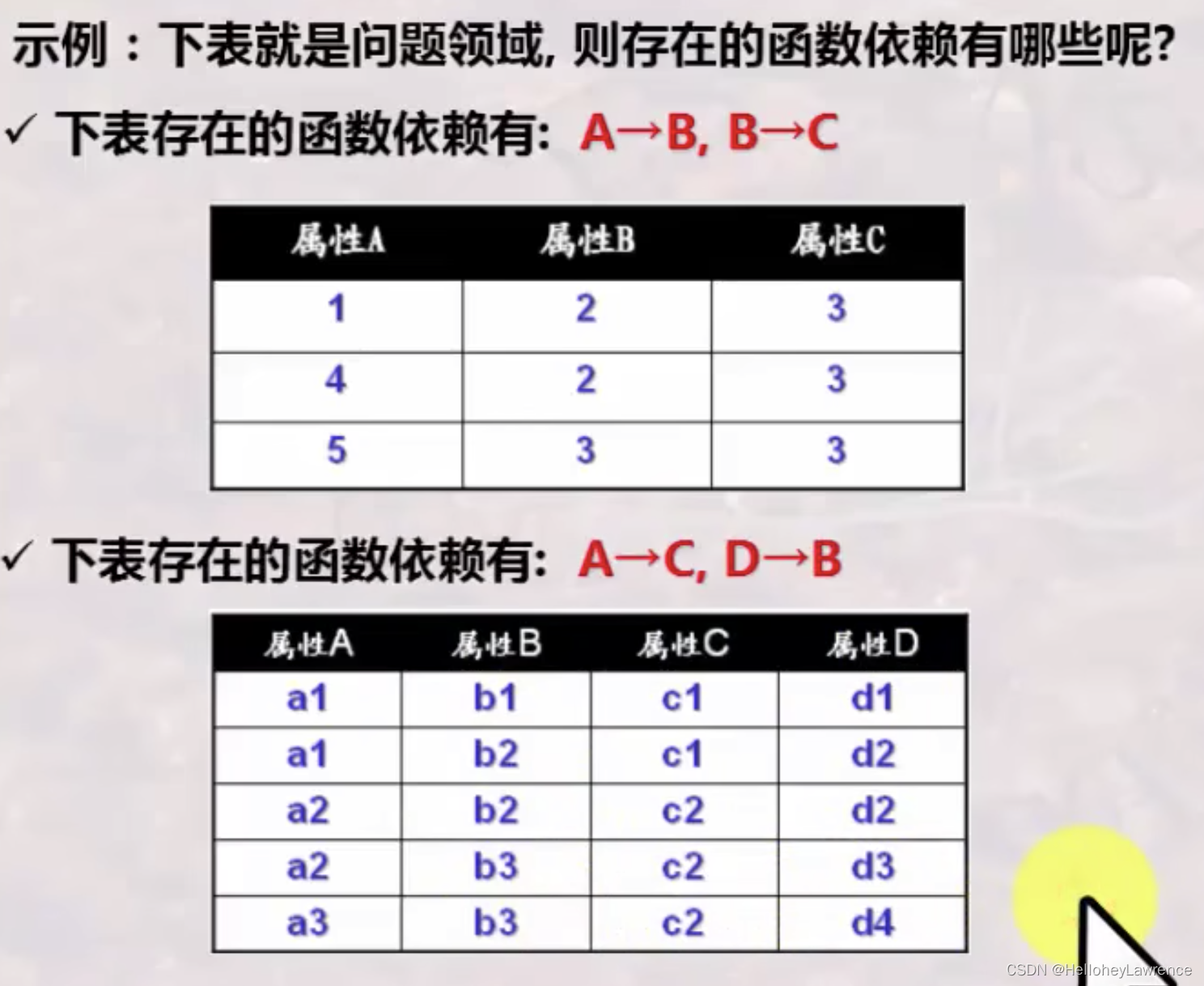



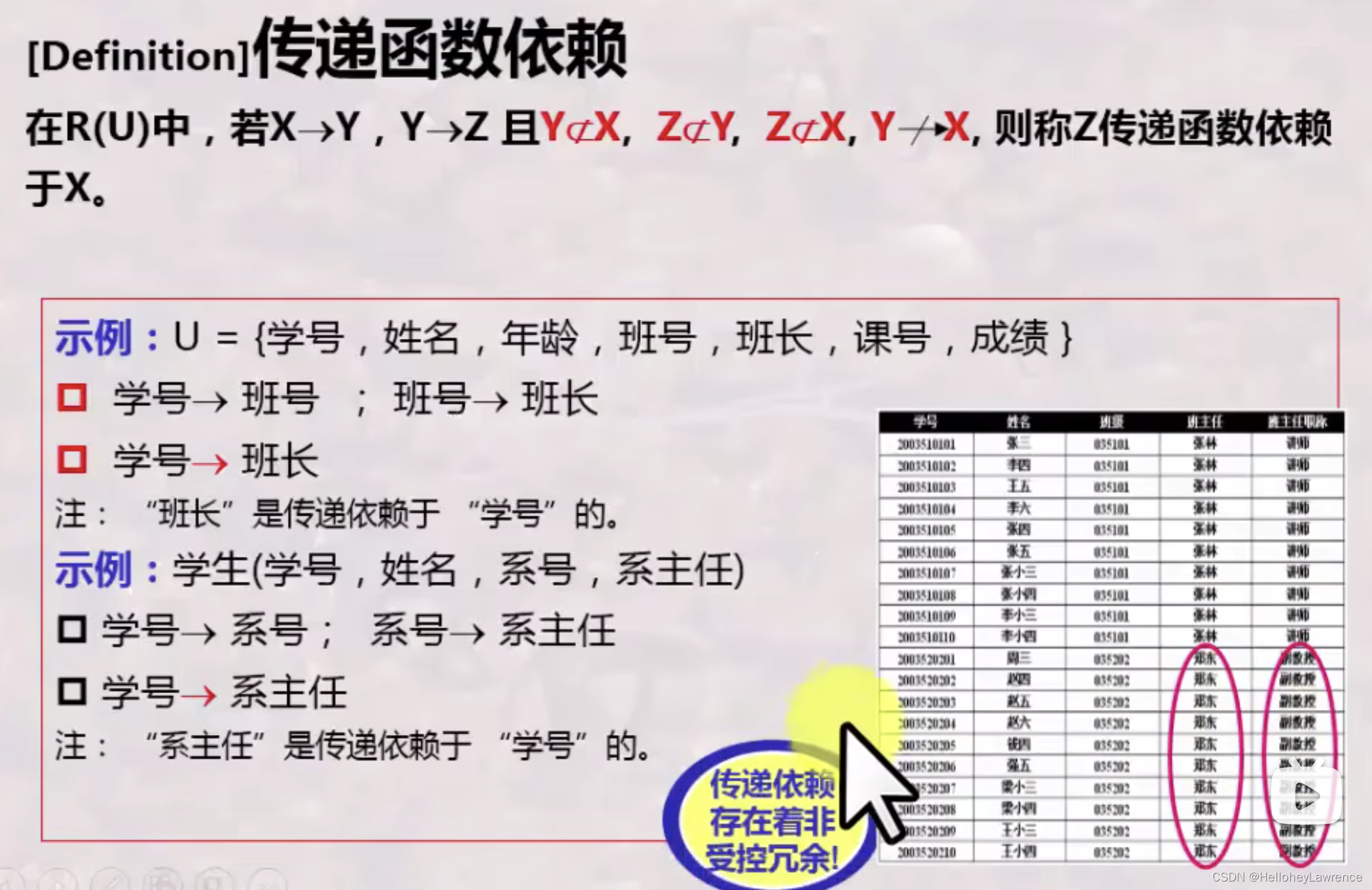
-
逻辑蕴涵(就是由F能推出来的函数依赖)

-
闭包F+

-
Armstrong 公理



-
属性集闭包
- 在判断能否从已知的FD集F推导出FD X—>Y,可以先求F的闭包F+,然后看FD X—>Y是否在这个闭包中。
- 但是求F的闭包是一个指数级时间问题、NP完全问题,所以引入属性集闭包的概念
- 如果Y在X关于F的属性集闭包(X+F)中,则可以根据F推出FD X—>Y。


-
FD集的最小依赖集(最小覆盖)



最小依赖集:
1)右边都是单个属性
2)没有冗余的函数依赖
3)每个函数依赖左边没有冗余的属性
每个函数依赖集FD 至少存在一个等价的最小依赖集,但不一定唯一。求最小依赖集G
1)把右边都分解为单个属性,如A —> BC,分解为A —> B,A —> C
2)消除每个FD 左边冗余的属性 ,如A —> C, AB —> C,消除 AB —> C
3)消除冗余的FD
顺序不能反! -
主属性是指包含在任何一个候选码中的属性
-
非主属性是不包含在任何候选码中的属性

4.2 关系模式的分解性
- 数据库模式
- 泛关系模式
- 泛关系
- 寄生元组:泛关系在按照分解的每一模式投影再重新连接后多出来的元组
- 泛关系假设:先存在r(泛关系),再去谈论分解
- 悬挂元组:在无泛关系假设时,对两个关系进行自然连接而丢失的元组
- 悬挂元组是造成两个关系不存在泛关系的原因
怎么理解泛关系假设:对于一个R(ABC),要对这个关系模式下的具体关系进行分解,也就是属性为ABC的关系。如果有个关系是AB,有个关系是BC,那么他们连接起来本来就可能丢失元组(悬挂元组),就没必要讨论无损分解了。

如果分解后再连接起来发现元组多了,这些多了的元组叫做寄生元组,多出来的是噪声,这样的分解就是有损分解,损指信息的损失,不是指元组的丢失,所以多了少了都不行。

m(m( r ))=m( r )的意思就是说 将m( r )也按照 ABC、BCD进行分解在连接,得到的还是m( r )
-
无损连接分解

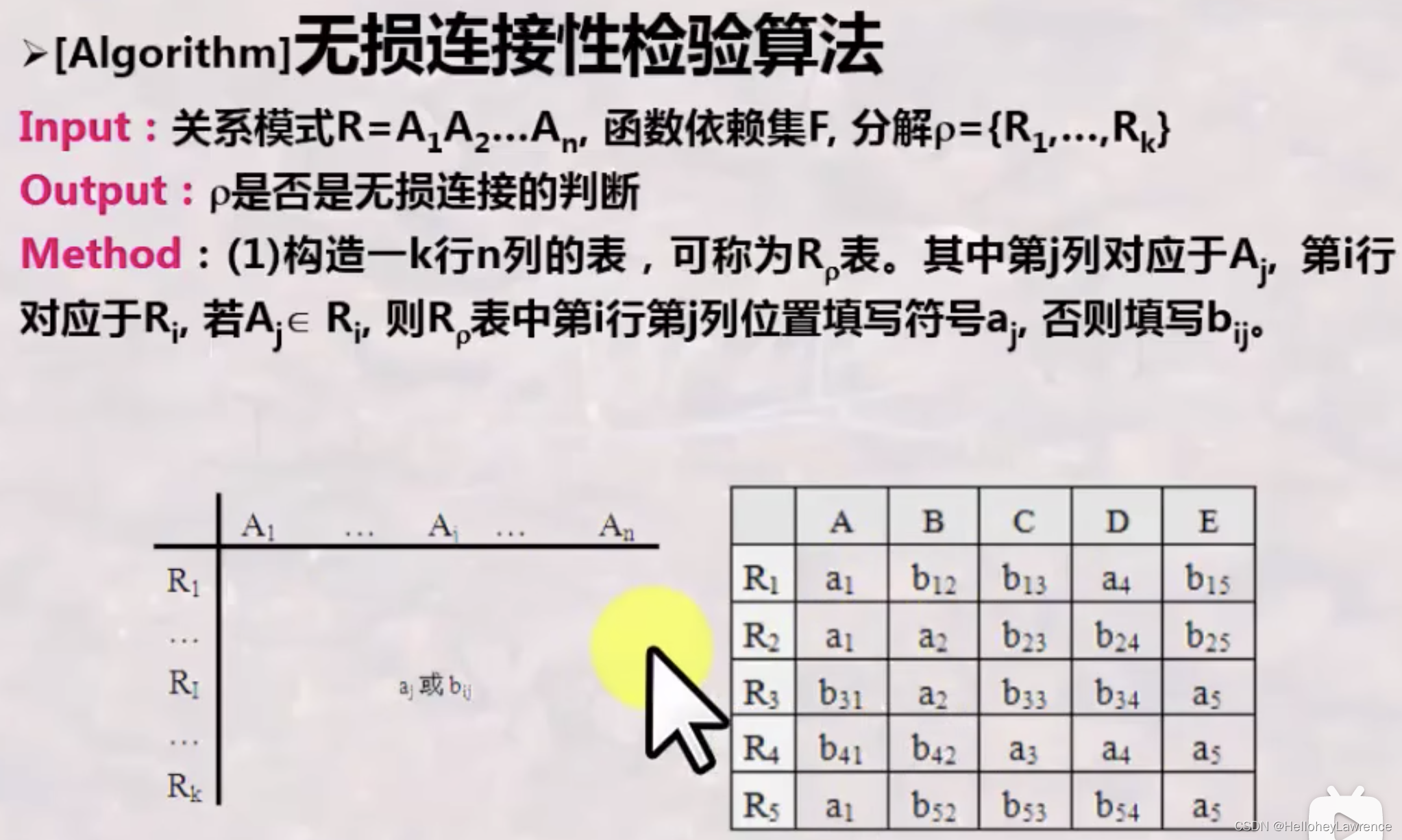
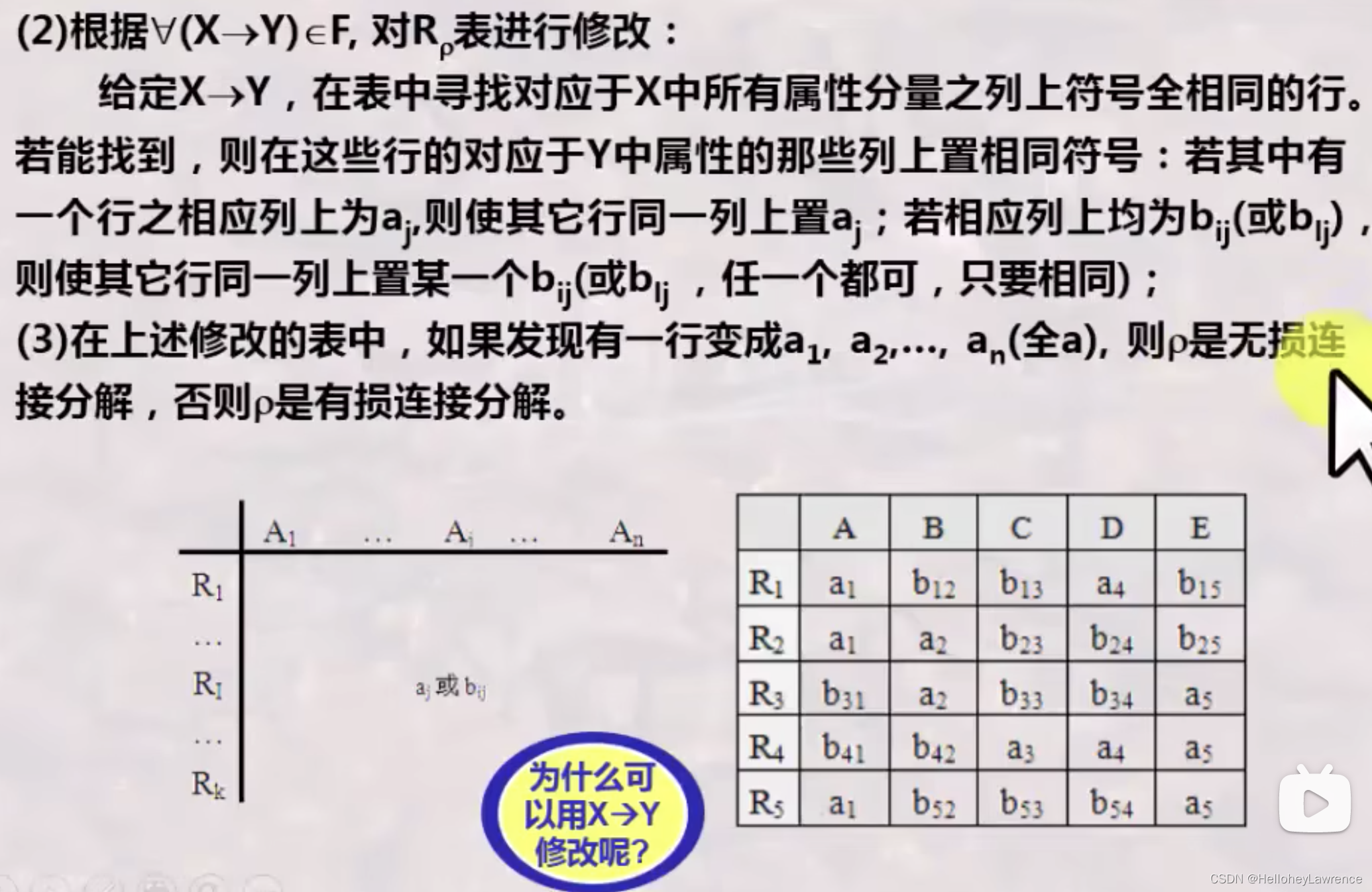
这里的FD要按照顺序写,否则下面修改的时候会修改不完全!
比如,Bid -> Bno , Bno -> Bname ; 这两个函数依赖隐含着传递性,顺序不能反!
看这个例子!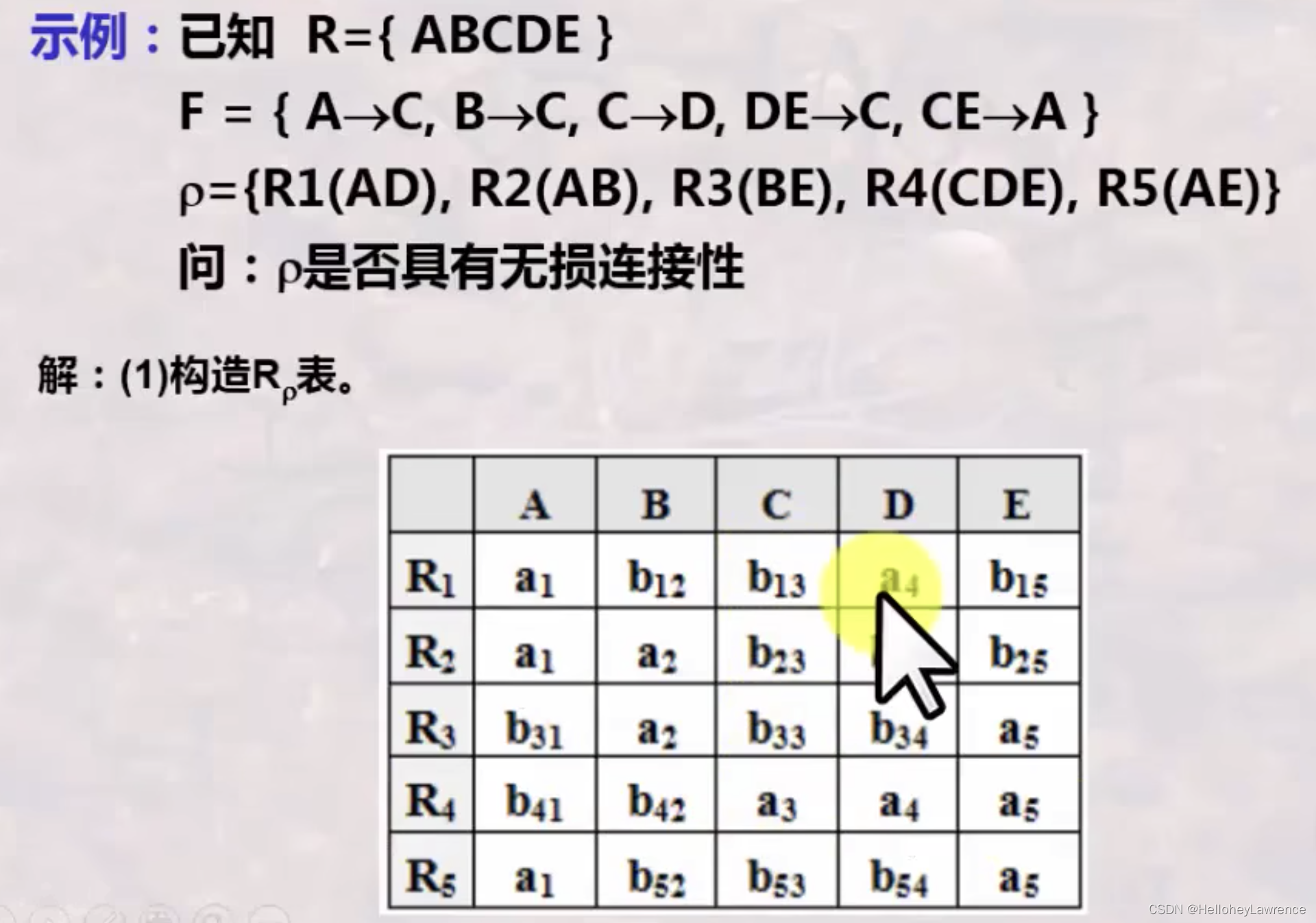
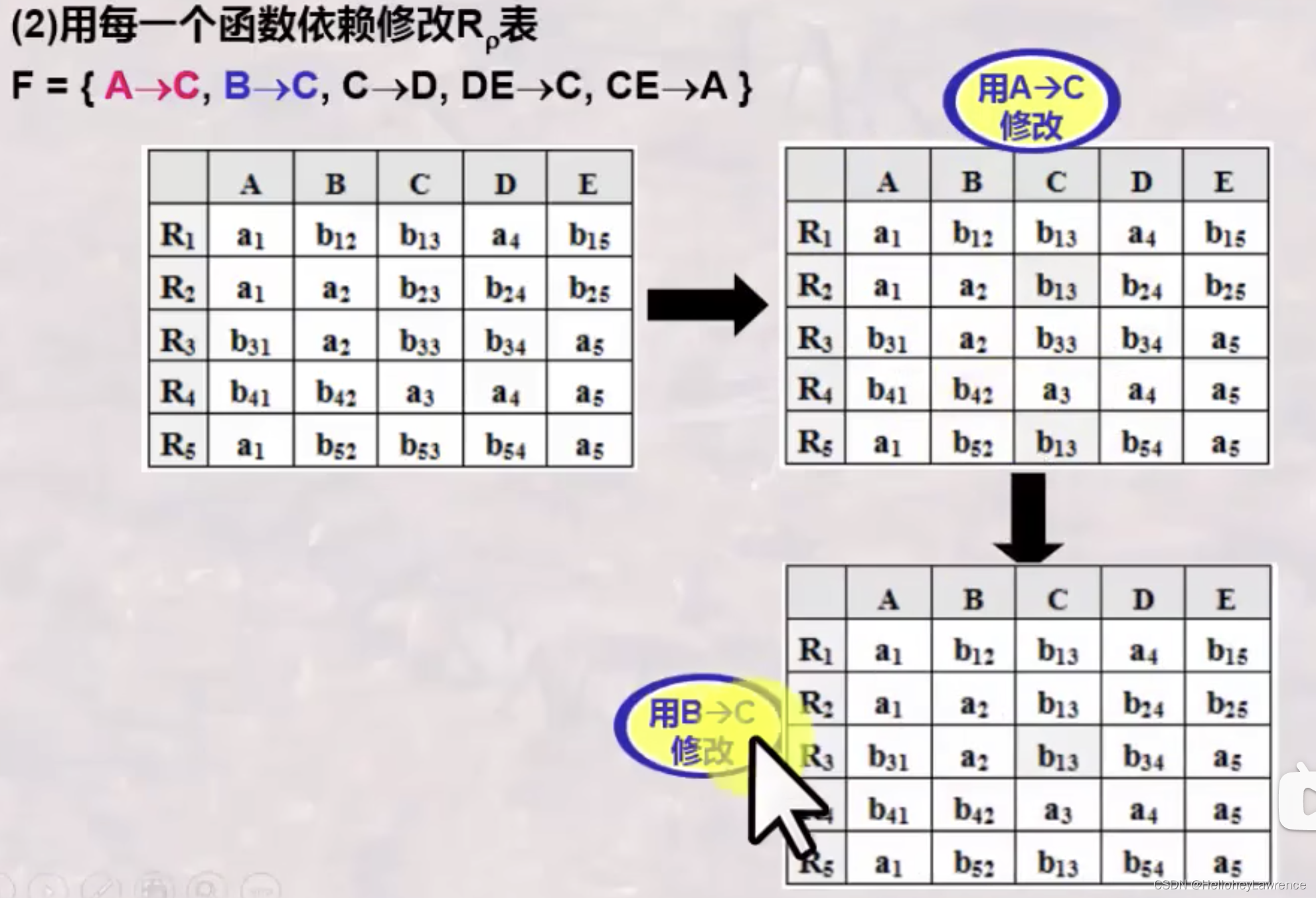
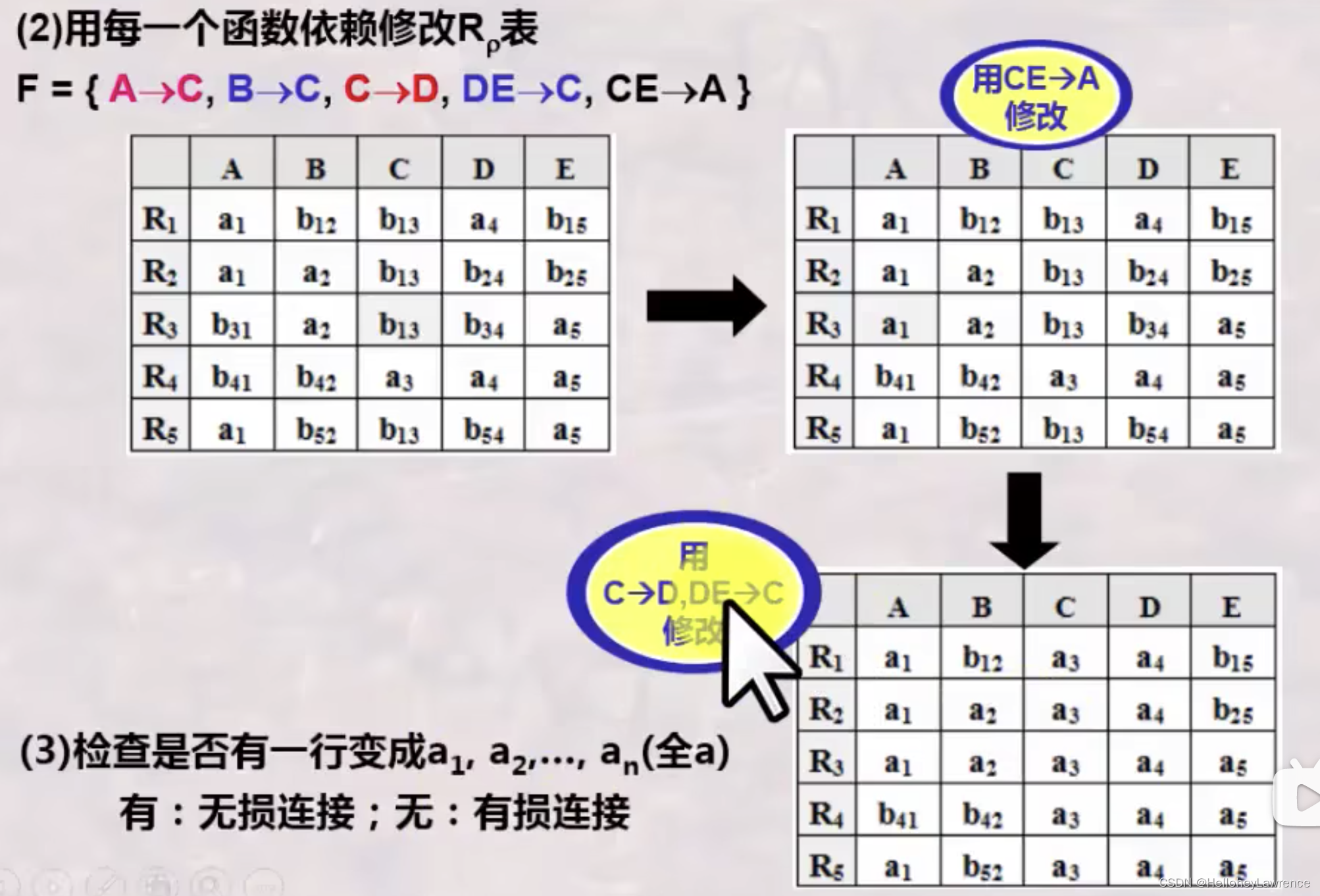
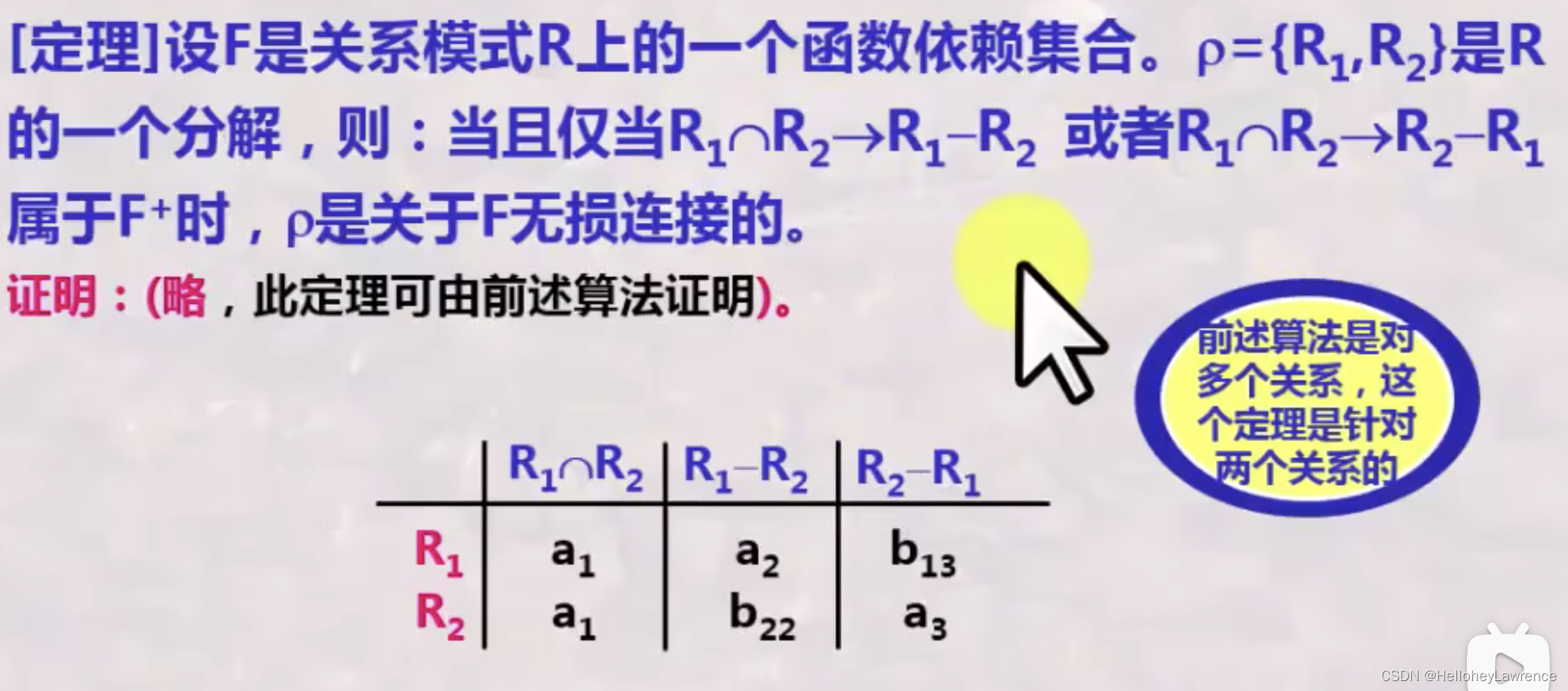

对一个无损连接的分解,如果把其中一个关系模式再进行无损连接分解,合在一起还是一个无损连接分解
对于一个包含了无损连接分解的另一个分解,依然是无损连接的 -
保持依赖分解



-
分解成BCNF模式集的分解算法


-
分解成3NF模式集的合成算法
将关系模式R无损分解且保持依赖的分解成3NF模式集- 先求出F的最小依赖集,再把最小依赖集中左部相同的FD合并
- 对最小依赖集中每个FD X->Y 构成一个模式XY
- 在构成的模式集中,如果每个模式不包含R的候选键,那么把候选键作为一个模式放到模式集中
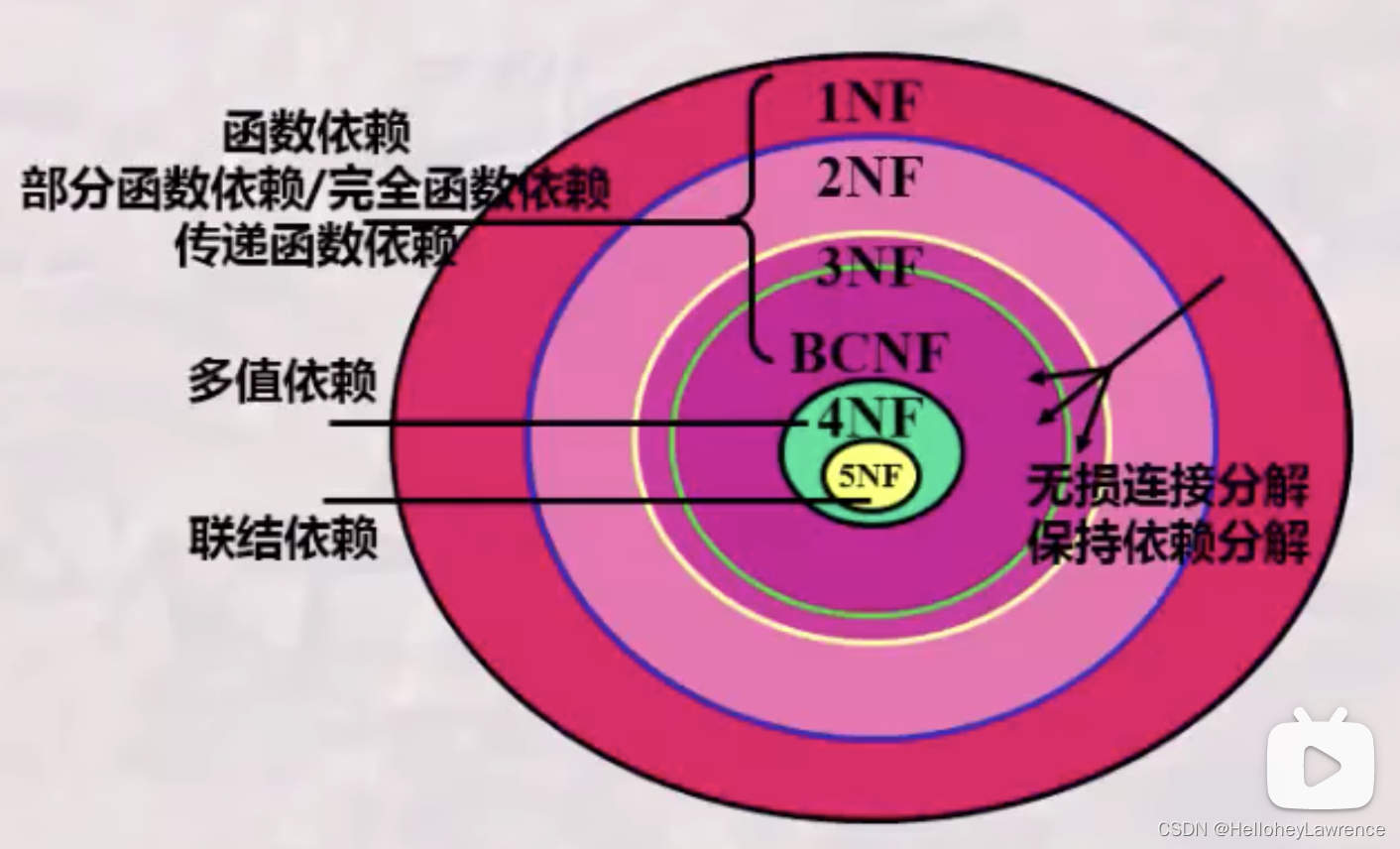
4.3 关系模式的范式
-
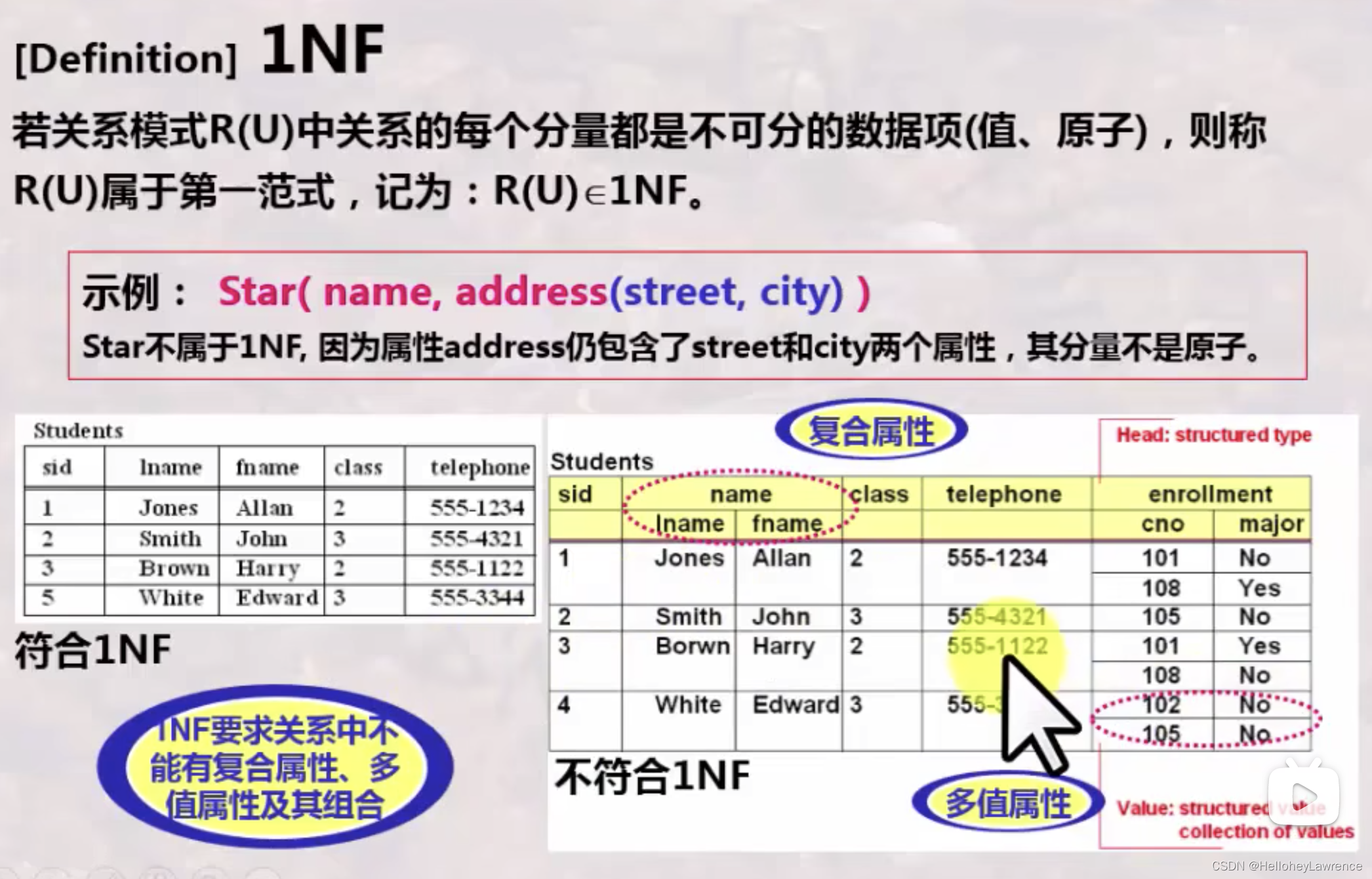
第一范式
满足1NF的关系叫做规范化的关系,否则叫做非规范化的关系
-
第二范式 (1NF + 非主属性完全依赖于候选码)


2,3、BCNF、4范式:看看这篇文章举的例子 -
第三范式(2NF + 消除了非主属性对于候选码的传递函数依赖)


-
BCNF(3NF + 消除主属性对于候选码的部分与传递函数依赖)

- 若一个关系模式符合BCNF,则一定符合3NF;
- 若一个关系模式不满足3NF,一定不满足BCNF;
- 定义中X必含有候选键的意思是包含候选键!意思是不能少!
-
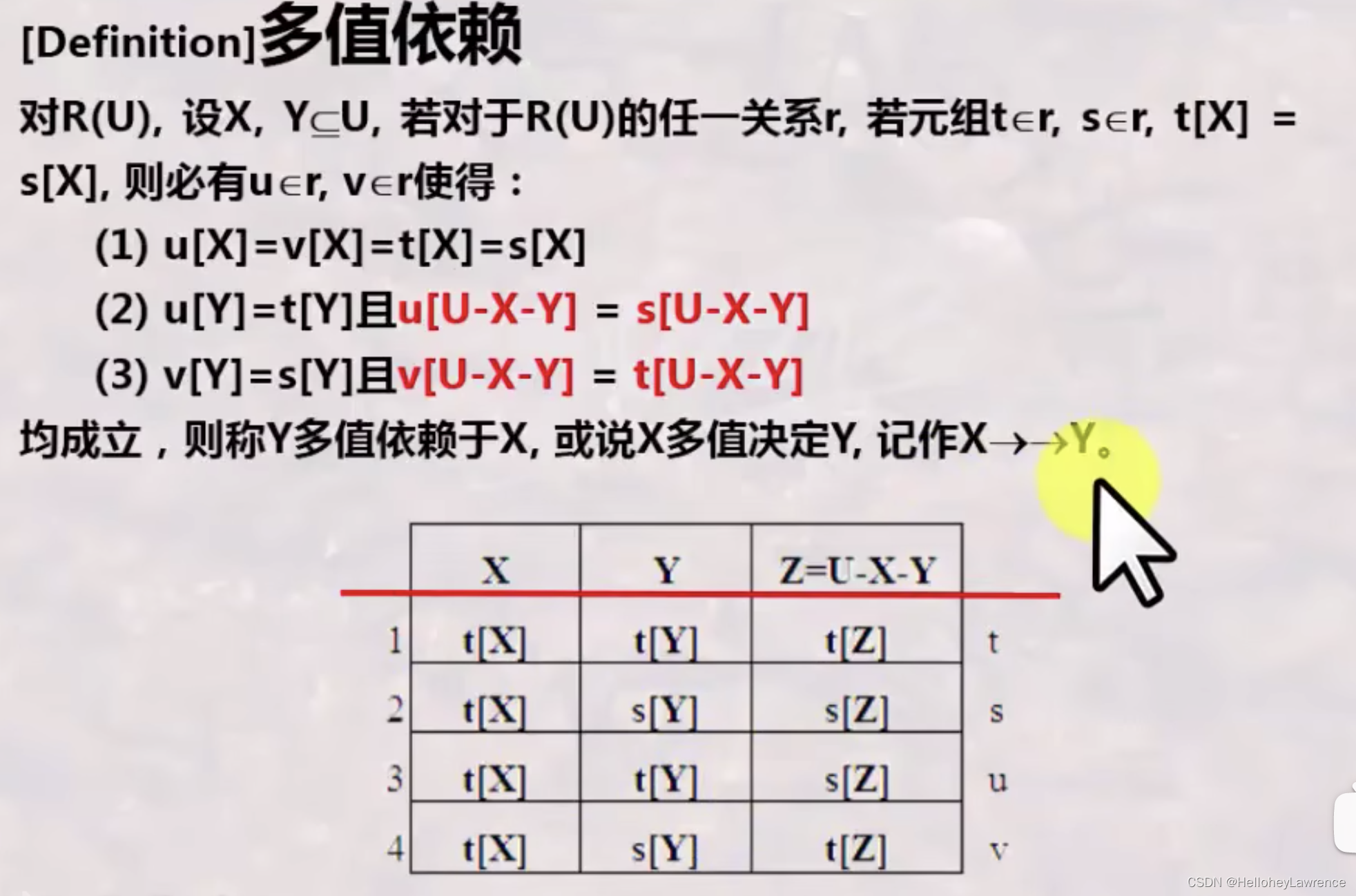
多值依赖
下面的定义太晦涩,看这个:多值依赖的解释



-
第四范式(消除了非主属性对候选键以外属性的多值依赖)

- 通俗的说,就是对于有三个属性的表,给定属性A一个值,剩余两个列之间不存在多对多的关系。
- 若满足4NF,则一定满足BCNF;
- 若R上仅存在函数依赖,则若有R满足BCNF,R一定满足4NF;反之,若R满足4NF,则R也满足BCNF;
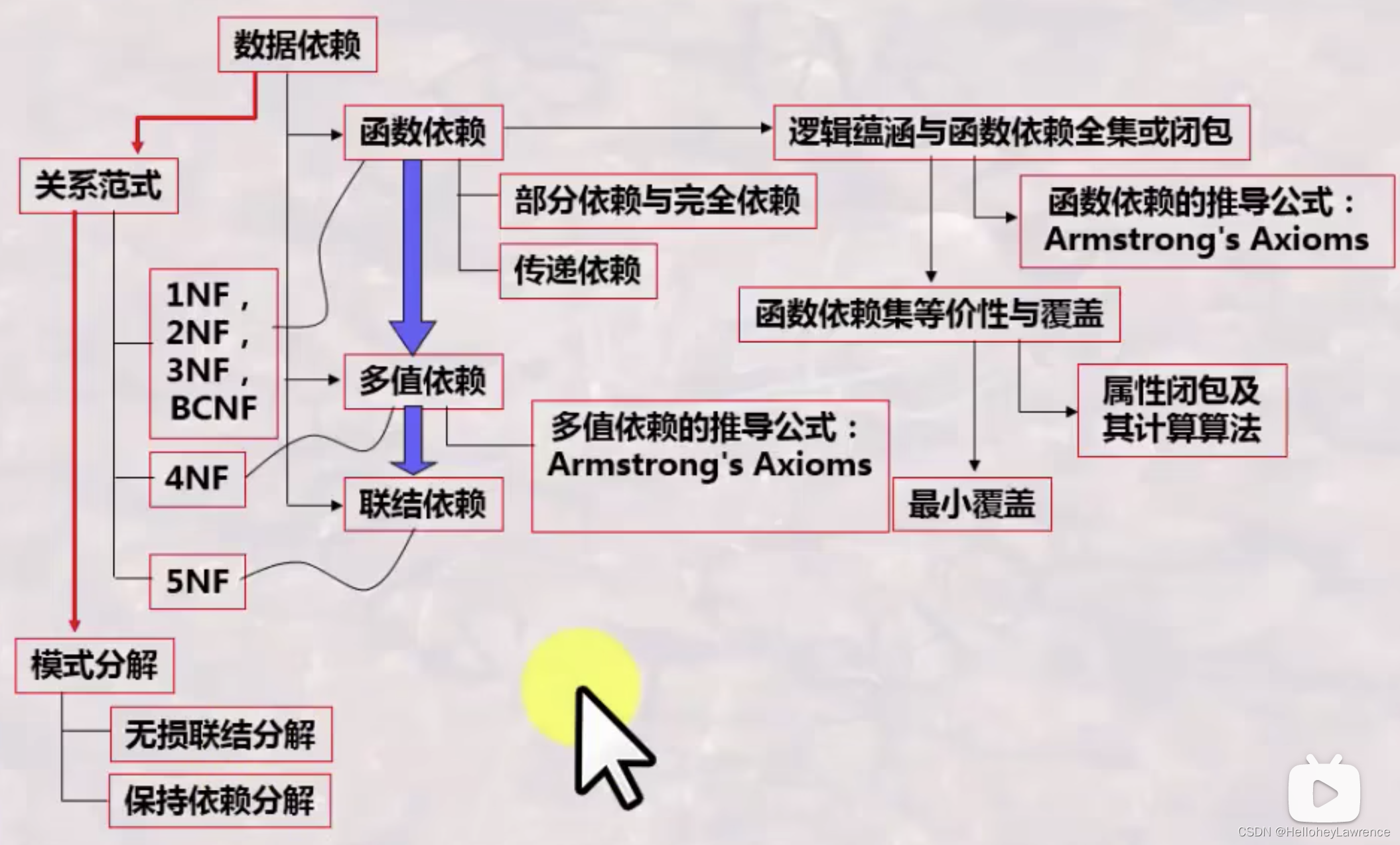




 本文介绍了数据库设计中的函数依赖概念,包括函数依赖的闭包、最小依赖集的求解方法,以及关系模式的分解性和范式等内容。通过实例解析如何进行无损连接分解和保持依赖分解,帮助读者深入理解规范化过程。
本文介绍了数据库设计中的函数依赖概念,包括函数依赖的闭包、最小依赖集的求解方法,以及关系模式的分解性和范式等内容。通过实例解析如何进行无损连接分解和保持依赖分解,帮助读者深入理解规范化过程。
















 9万+
9万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








