代码随想录：动态规划问题

动态规划

动态规划五步曲：
1.确定dp数组以及下标的含义
2.确定递推公式
3.dp数组如何初始化
4.确定遍历顺序
5.举例推导dp数组

10.1日任务：斐波那契数

首先想到的是递归，试试，没有什么问题
class Solution {
public:
    int fib(int n) {
        //递归更简单
        if (n == 0) return 0;
        if (n == 1) return 1;
        //顺序
        return fib(n - 1) + fib(n - 2);
    }
};
代码随想录的思路：
class Solution {
public:
    int fib(int n) {
        //最简单的方法是递归
        //在这里使用动态规划进行体验
        //动态规划的翻译：dynamic programming
        //第一步：确定dp数组的含义:dp[i]代表斐波那契数列的第i个数
        //第二步：确定递推公式：F(n) = F(n - 1) + F(n - 2)
        //第三步：dp数组如何初始化：dp[0] = 0, dp[1] = 1.
        //第四步：遍历顺序：从前往后(从小往大)
        //第五步：举例推导： 0 1 1 2 3 5 8 13 21 34

        //特殊情况考虑，其实就是初始化的东西
        if (n == 0) return 0;
        else if (n == 1) return 1; 
        //定义dp数组
        vector<int> dp(n + 1 , 0);
        //初始化
        dp[0] = 0;
        dp[1] = 1;
        //遍历
        for (int i = 2; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
};
更低空间复杂度的写法：
class Solution {
public:
    int fib(int n) {
        //最简单的方法是递归
        //在这里使用动态规划进行体验
        //动态规划的翻译：dynamic programming
        //第一步：确定dp数组的含义:dp[i]代表斐波那契数列的第i个数
        //第二步：确定递推公式：F(n) = F(n - 1) + F(n - 2)
        //第三步：dp数组如何初始化：dp[0] = 0, dp[1] = 1.
        //第四步：遍历顺序：从前往后(从小往大)
        //第五步：举例推导： 0 1 1 2 3 5 8 13 21 34

        //特殊情况考虑，其实就是初始化的东西
        if (n == 0) return 0;
        else if (n == 1) return 1; 
        //定义dp数组
        vector<int> dp(2, 0);
        //初始化
        dp[0] = 0;
        dp[1] = 1;
        //遍历
        int temp = 0;
        for (int i = 2; i <= n; i++) {
            temp = dp[0] + dp[1];
            dp[0] = dp[1];
            dp[1] = temp;
        }
        return temp;
    }
};

10.2日任务：爬楼梯

和斐波那契数的递推公式一模一样，比较简单，基础题是用来入门理解动态规划的。
第一步：确定dp数组下标含义.
第二步：确定递推公式.
第三步：dp数组如何初始化
第四步：遍历顺序
第五步：举例推导
递推公式的产生，也是需要对于问题有深刻的理解之后才能产生，明显感觉到后面数据结构的编程模式已经很简单了，难的是对于具体问题的理解。

class Solution {
public:
    int climbStairs(int n) {
        //按照代码随想录给的思路：
        //找规律: n=1，1个台阶一步爬; n=2,2个台阶一步爬或者1个台阶两部爬；n = 3,可以从n=2跨一个台阶，或者从n=1跨2个台阶
        //从规律可得dp[n] = dp[n-1] + dp[n-1] n>2
        if (n <= 2) return n;
        //第一步，确定dp数组的索引含义：dp[i]代表第n = i 时，有几种不同方法爬到楼顶
        vector<int> dp(2,0);
        //第二步：递推公式:dp[n] = dp[n-1] + dp[n-1] n>2
        //第三步：初始化
        dp[0] = 1;
        dp[1] = 2;
        //遍历顺序，从前往后
        int temp = 0;
        for (int i = 3; i <= n; i++) {
            temp = dp[0] + dp[1];
            dp[0] = dp[1];
            dp[1] = temp;
        }
        return temp;
    }
};

10.3号任务：使用最小花费爬楼梯

按照自己的思路编写，动态规划核心就是针对问题的理解，只要递推公式出来了就问题不大。
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //由题目可知：2 <= cost.length <= 1000
        //考虑dp[i]下标的含义：爬上第i个台阶需要花费的最小费用
        //递推公式： 第n个台阶可以通过第n-1个台阶爬一阶或者第n-2个台阶爬两阶得到。
        //dp[n] = min(dp[n-1]+cost[n-1],dp[n-2]+cost[n-2])
        //已经默认2 <= cost.length <= 1000
        vector<int> dp(cost.size() + 1, 0);
        //初始化dp
        dp[0] = dp[1] = 0;
        //遍历顺序，由小到大遍历
        for (int i = 2; i <= cost.size(); i++) {
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        //举例推导
        //针对[1,100,1,1,1,100,1,1,100,1]，dp数组推导结果为[0 0 1 2 2 3 3 4 4 5 6]
        return dp[cost.size()];
    }
};
节省空间的写法：
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        //由题目可知：2 <= cost.length <= 1000
        //考虑dp[i]下标的含义：爬上第i个台阶需要花费的最小费用
        //递推公式： 第n个台阶可以通过第n-1个台阶爬一阶或者第n-2个台阶爬两阶得到。
        //dp[n] = min(dp[n-1]+cost[n-1],dp[n-2]+cost[n-2])
        //已经默认2 <= cost.length <= 1000
        vector<int> dp(2, 0);
        //初始化dp
        dp[0] = dp[1] = 0;
        //遍历顺序，由小到大遍历
        int temp = 0;
        for (int i = 2; i <= cost.size(); i++) {
            temp = min(dp[0] + cost[i - 2], dp[1] + cost[i - 1]);
            dp[0] = dp[1];
            dp[1] = temp;
        }
        //举例推导
        //针对[1,100,1,1,1,100,1,1,100,1]，dp数组推导结果为[0 0 1 2 2 3 3 4 4 5 6]
        return temp;
    }
};

10.3号任务（当日第二题）：不同路径

目前第一遍学习仅掌握基本的动态规划方法就好了，其他的二刷的时候再来搞。

按照自己的思路独立编写：只要遵循动态规划的流程来思考，整体还是比较轻松的
class Solution {
public:
    int uniquePaths(int m, int n) {
        //核心是dp数组的递推公式以及遍历顺序，这个是一个二维dp数组
        //第一步：dp数组的下标的含义：dp[i][j]指机器人到达i行j列有多少条不同的路径
        //递推公式: dp[i][j] = dp[i-1][j] + dp[i][j-1] (i >= 1, j >= 1)
        //dp[i][j] = dp[i][j - 1] (i=0,j>=1)
        //dp[i][j] = dp[i - 1][j] (j=0,i>=1)
        //dp[0][0] = 1;
        //返回值为dp[m-1][n-1]
        vector<vector<int>> dp(m, vector<int>(n,0));
        //初始化
        dp[0][0] = 1;
        //遍历顺序：逐行遍历
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j == 0) dp[i][j] = 1;
                else if (i == 0 && j > 0) dp[i][j] = dp[i][j - 1];
                else if (i > 0 && j == 0) dp[i][j] = dp[i-1][j];
                else dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        //举例推导：前期推导递推公式的时候已经简单举例推过了
        return dp[m - 1][n - 1];
    }
};

10.3号任务（当日第三题）：不同路径II

和上一道题几乎一模一样，多了个限制条件而已，目前掌握一种写法即可。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        //确定dp数组的含义：dp[i][j]指机器人到达i行j列有多少条不同的路径，obstacleGrid为1则dp值为0
        //递推公式: obstacleGrid[i][j] == 1 dp[i][j] = 0;
        //dp[i][j] = dp[i-1][j] + dp[i][j-1] (i >= 1, j >= 1)
        //dp[i][j] = dp[i][j - 1] (i=0,j>=1)
        //dp[i][j] = dp[i - 1][j] (j=0,i>=1)
        //dp[0][0] = 1;
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        //初始化就包含在遍历里了
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (obstacleGrid[i][j] == 1) dp[i][j] = 0;
                else if (i == 0 && j == 0) dp[i][j] = 1;
                else if (i == 0 && j > 0) dp[i][j] = dp[i][j - 1];
                else if (i > 0 && j == 0) dp[i][j] = dp[i-1][j];
                else dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        //举例推导：前期推导递推公式的时候已经简单举例推过了
        return dp[m - 1][n - 1];

    }
};

10.3日任务（当日第四题）：整数拆分

这道题比较开阔思路的，递推公式还是要看个人对于问题理解了多少。这道问题的dp数组更新是多次比较得来的，而不是简单的直接公式推导，这点比较扩展思路，这道题挺不错。动态规划的题目，本质上还是看对于问题是否理解了，只要思路明确了，问题就解决了。

class Solution {
public:
    int integerBreak(int n) {
        //直接看代码随想录的思路，我想了20分钟没想出来什么东西
        //确定dp数组下标的含义：分拆数字i，可以得到的最大乘积为dp[i]
        //递推公式：dp[i] = max(dp[i], max(j * (i - j), j * dp[i-j]));
        //递推公式解释：分拆数字i得到dp[i]的途径有两种：j * (i - j)为两数相乘，j * dp[i-j]为多个数相乘
        //递推公式这里求dp[i]没有什么特别的规律（dp数组前后联系的规律），只好用不断比较大小来作为递推公式，这个还是比较扩展思路的，算是一种复杂递推公式的形式。
        vector<int> dp(n+1,0);
        //dp[0],dp[1]没有什么含义
        //遍历顺序，从前向后
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < i; j++) {
                dp[i] = max(dp[i], max(j * (i - j), j * dp[i-j]));
            }
        }
        return dp[n];
    }
};

10.4日任务：不同的二叉搜索树

10.3号做题过量了，把握一个重点：脑袋最清醒的时候去干掉最难最磨人的科研，脑袋咪咪呼呼的时候用刷题来提神延长注意力，刷完题去做晚间运动。刷题放在下午吃完饭会微微犯困的时侯。
只要问题递推关系研究清楚了，动态规划问题就解决了。

class Solution {
public:
    int numTrees(int n) {
        //按照代码随想录的思路自己来
        //第一步：dp下标的含义：dp[n]代表给定整数n时，满足题意得二叉搜索树的种树。
        //递推公式：
        //dp数组初始化
        if (n < 3) return n;
        vector<int> dp(n+1,0);
        dp[1] = 1;
        dp[2] = 2;
        //遍历顺序，自前向后
        for (int i = 3; i < n + 1; i++)
        {
            dp[i] = 2 * dp[i - 1];
            for (int j = 1; j < i - 1; j++) {
                dp[i] = dp[i] + dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
};
换一种写法：
class Solution {
public:
    int numTrees(int n) {
        //按照代码随想录的思路自己来
        //第一步：dp下标的含义：dp[n]代表给定整数n时，满足题意得二叉搜索树的种树。
        //递推公式：
        //dp数组初始化
        if (n < 3) return n;
        vector<int> dp(n+1,0);
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;
        //遍历顺序，自前向后
        for (int i = 3; i < n + 1; i++)
        {
            for (int j = 0; j < i; j++) {
                if (j == 0 || j == i - 1) {
                    dp[i] = dp[i] + max(dp[j],dp[i - j - 1]);
                }
                else dp[i] = dp[i] + dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
};
dp[0] = 1 的话会更简单。
class Solution {
public:
    int numTrees(int n) {
        //按照代码随想录的思路自己来
        //第一步：dp下标的含义：dp[n]代表给定整数n时，满足题意得二叉搜索树的种树。
        //递推公式：
        //dp数组初始化
        if (n < 3) return n;
        vector<int> dp(n+1,0);
        dp[0] = 1;
        dp[1] = 1;
        dp[2] = 2;
        //遍历顺序，自前向后
        for (int i = 3; i < n + 1; i++)
        {
            for (int j = 0; j < i; j++) {
                dp[i] = dp[i] + dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
};

10.5日任务：背包理论基础（一）

今天是背包问题基础理论，先看解析，再按照自己的思路独立编写。
特殊问题差点没注意到：这个代码这里我第一次着急，没有意识到用if和else.

索引为负数时，最后产生的是一个错误的负数。数组索引问题要注意，索引为负数时，编译器运行是不会报错的。
如果出现这个问题，可能会造成非常大的影响。
dp[i - 1][j - takeUpSpace[i]]

#include<iostream>
#include<vector>
#include<unordered_set>
#include<algorithm>
using namespace std;

int main() {
	//下来开始编写0-1背包问题代码，对应卡码网0-1背包问题
	int M,N; //M代表研究材料的种类，N代表小明的行李空间
	cin >> M >> N;
	vector<int> takeUpSpace(M, 0);
	vector<int> value(M, 0);
	for (int i = 0; i < M; i++) cin >> takeUpSpace[i];
	for (int i = 0; i < M; i++) cin >> value[i];
	//按照动态规划的步骤走：
	//1.确定dp数组下标的含义
	vector<vector<int>> dp(M, vector<int>(N + 1, 0));
	//dp数组下标含义如下：dp[i][j]代表将0-i号研究材料放入到行李空间为j的背包中得到的最大价值
	//2.确定递推公式：dp[i][j]可以分成两种放法：第一种：行李空间为j的背包中不放i号研究材料（即仅放置0到i-1号材料）。
	// 第二种是行李空间为j的背包中必须放置第i号研究材料
	//对于第一种方案：最大价值也对应的是dp[i-1][j]的数值
	//对应第二种方案：最大价值对应的是value[i]+dp[i-1][j - takeUpSpace[i]]
	//d[i][j]取的是两种方案的最大值，即递推公式为dp[i][j] = max(dp[i-1][j],value[i]+dp[i-1][j - takeUpSpace[i]])
	//3.dp数组初始化：对于第一列即行李空间为0的时候，所有研究材料都无法放下，最大价值即为0;对于第一行:takeUpSpace[0]>j即研究材料0可以放进去，最大价值为研究材料0的价值
	//先初始化第一列
	for (int i = 0; i < M; i++) dp[i][0] = 0;//这句话其实可以不写的，因为定义数组时这里已经初始化为0了
	//再初始化第一行
	for (int i = 0; i <= N; i++) {
		if (takeUpSpace[0] > i) dp[0][i] = 0;
		else dp[0][i] = value[0];
	}
	//4.遍历顺序，先横向由低向高遍历，再竖向由低到高遍历
	for (int i = 1; i < M; i++) {
		for (int j = 1; j <= N; j++) {
			if (takeUpSpace[i] > j) dp[i][j] = dp[i - 1][j];
			else dp[i][j] = max(dp[i - 1][j], value[i] + dp[i - 1][j - takeUpSpace[i]]);
		}
	}
	cout << dp[M - 1][N];
	return 0;
}

10.6日任务：背包理论基础（二）

今天的任务是背包理论基础（一）的简化版，从二维数组降级为一维数组，简化问题，简化空间复杂度。
根据代码随想录的思路直接敲代码。
比较简单，没有什么大难度。
#include<iostream>
#include<vector>
#include<unordered_set>
#include<algorithm>
using namespace std;

int main() {
	//下来开始编写0-1背包问题代码，对应卡码网0-1背包问题
	int M,N; //M代表研究材料的种类，N代表小明的行李空间
	cin >> M >> N;
	vector<int> takeUpSpace(M, 0);
	vector<int> value(M, 0);
	for (int i = 0; i < M; i++) cin >> takeUpSpace[i];
	for (int i = 0; i < M; i++) cin >> value[i];
	//按照动态规划的步骤走：
	//1.确定dp数组下标的含义（这种方法是一个一维数组，或者说是一个滚动数组）
	//dp[i][j]是编号为0-i的研究材料放入行李空间j中产生的最大价值
	//dp[j]这个数组每个元素不是仅更新一次，而是M次，因为有M种研究材料，第i次更新dp[j]相当于将编号为0-i的研究材料放入行李空间j中产生的最大价值。
	vector<int> dp(N + 1, 0);
	//2.递推公式 dp[i][j] = max(dp[i-1][j],value[i]+dp[i-1][j-takeUpSpace[i]]); takeUpSpace[i]<=j;
	//由于递推公式dp[i][j]的更新依赖于dp[i-1][j]所代表的行，并且依赖的是是该行下标为0-j的元素。可以考虑将dp[i][j]在更新下标为i的行时，dp[i][j]已经被复制为dp[i-1][j]
	//递推公式可以看作：dp[j] = max(dp[j],value[i]+dp[j-takeUpSpace[i]]);
	//3.初始化
	//既可以全部初始化为0，也可以先初始化第一行，无所谓，先全部初始化为0即可。定义dp的时候已经全部初始化过了。
	//4.遍历顺序：从后往前遍历，这是因为由于递推公式dp[i][j]的更新依赖于dp[i-1][j]所代表的行，并且依赖的是是该行下标为0-j的元素。
	//所以说遍历dp[j]时要用到上一轮更新过的下标为0-j的值
	for (int i = 0; i < M; i++) {
		for (int j = N; j >= 1; j--) {
			if (takeUpSpace[i] > j) dp[j] = dp[j];
			else dp[j] = max(dp[j], value[i] + dp[j - takeUpSpace[i]]);
		}
	}
	cout << dp[N];
}

10.7日任务（10.7日去爬山，10.6日下午补一下）：分割等和子集

到了后面的题目之后，一旦你掌握了动态规划理论的本质，只要你能够将问题转化为背包问题，代码层面不是问题。所以看完代码随想录的思路之后就可以开始写代码了，不用去参考代码随想录的代码，重要的是保证自己思维的独立性。
这道题的遍历是可以提前结束的，只要保证自己思维的独立性，就可以产生比代码随想录思路更好的点。

按照代码随想录的思路独立编写
class Solution {
public:
    bool canPartition(vector<int>& nums) {
        //简单看了一会，我自己是没有任何思路的
        //按照代码随想录的思路来看，找存不存在一个子集的和等于所有数总和的一半
        //整个问题的第一阶段：求和看这个数组之和是不是偶数
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        if (sum % 2 != 0) return false;
        //如果是偶数的话，背包问题背包的容量为sum/2,物品的重量为数组的元素值，物品的价值也是数组的元素值
        //如何理解物品的价值也是数组的元素值呢？01背包问题是为了在有限的空间中装到到最大价值的物品。
        //当物品的价值也是数组的元素值时，那么背包容量为sum/2所能装到的最大价值也为sum/2。一般情况下只会<=sum/2
        //这道题的特殊之处在于我只要发现最大价值为sum/2时就可以结束循环了，不需要遍历所有元素
        //按照动态规划的步骤来：
        //第一步：确定dp数组的含义.dp[j]代表将0-i序号的物品放入容量为j的背包里,所能达到的最大价值，这道题里就是0-i个元素放入容量为j的背包里所能达到的最大和，最大和为j说明，背包刚好放满
        vector<int> dp(sum / 2 + 1,0);
        //递推公式：dp[j] = max(dp[j],nums[i]+dp[j - nums[i]]) nums[i]<=j;
        //初始化：第一行全部初始化为0就好了
        //遍历顺序：01背包问题前面已经推理过了是从后向前遍历
        for (int i = 0; i < nums.size(); i++) {
            for (int j = sum / 2; j >= 0; j--) {
                if (nums[i] > j) dp[j] = dp[j];
                else dp[j] = max(dp[j],nums[i] + dp[j-nums[i]]);
                if (j == sum / 2 && dp[j] == j) return true;
            }
        }
        return false;
    }
};

10.6日多刷一道：最后一块石头的重量II

这道题的核心还是转换到将所有石头分成重量最接近的两堆，两堆之差就是最终剩下石头的最小可能重量。只要这一步思路通了，就没什么问题了。

class Solution {
public:
    int lastStoneWeightII(vector<int>& stones) {
        //首先考虑的是把它转化为动态规划问题，更具体一点，先考虑转化为01背包问题
        //丝毫没有一丁点思路，直接看代码随想录的解析
        //代码随想录真的是一点就通：这道题本质就是将所有石头分成重量最接近的两堆，两堆之差就是最终剩下石头的最小可能重量
        //先求和
        int sum = 0;
        for(int i = 0; i < stones.size(); i++) {
            sum += stones[i];
        }
        //背包的最大容量如何设置呢？sum/2?
        //dp数组下标的含义：dp[j] 0-i号石头装进容量为j的背包里获得的最大价值,或者说能放进背包的最大重量
        vector<int> dp(sum / 2 + 1, 0);
        //递推公式：dp[j] = max(dp[j],stones[i] + dp[j - stones[i]]) stones[i] < j
        //初始化，已经初始化为0了
        //遍历顺序，自后向前遍历
        for (int i = 0; i < stones.size(); i++) {
            for (int j = sum / 2; j >= 0; j--) {
                if (stones[i] <= j) dp[j] = max(dp[j], stones[i] + dp[j - stones[i]]);
                if (j == sum/2 && dp[j] == j) break;
            }
            if (dp[sum / 2] == sum / 2) break;
        }
        //举例推导：纸上推导过了
        //返回值如何计算：sum - dp[sum/2] - dp[sum/2]
        //返回值计算：多的那一堆的重量减去少的这一堆的重量
        return sum - dp[sum / 2] - dp[sum / 2]; 
    }
};
其中遍历部分可以再精简一些：
        for (int i = 0; i < stones.size(); i++) {
            for (int j = sum / 2; j >= stones[i]; j--) {
                dp[j] = max(dp[j], stones[i] + dp[j - stones[i]]);
                if (j == sum/2 && dp[j] == j) break;
            }
            if (dp[sum / 2] == sum / 2) break;
        }

这道题的本质用数学原理来解释是比较有说服力的。

10.8日9日任务：目标和（题目难了些，用了两天）

题目本身比较复杂，是一个先推理简单的数学公式，然后转换到动态规划问题上，并且动态规划用的也不是简单的0-1背包问题，而是需要仔细分析问题，通过举例推导发现规律总结出递推公式才能得到。这道题目就比较综合，比较破除套路，偏向于灵活运用。还是比较考验解决问题的能力和对于算法本身的灵活运用的。综合来看，是一道非常不错的题目。

方法一：二维dp数组
按照代码随想录的思路，同时参考了代码。
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        //直接按照代码随想录的思路来：
        //不要啥都往0-1背包问题上想，这道题是一个有公式推导的动态规划问题，但不是0-1背包问题
        //因为一部分数保留为正数，另一部分数保留为负数
        //设正数部分的和为pos,负数部分的和为neg
        //pos - neg = target; pos + neg = sum; pos - (sum - pos) = target; pos = (sum + target) / 2
        //pos一定是一个整数, sum + target一定是一个偶数
        //先求和：
        int sum = 0;
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        if ((sum + target) % 2 != 0 || abs(target) > sum) return 0;
        sum = (sum + target) / 2;
        //接下来这个问题转化为nums数组中的元素，有多少种组合方式可以使得元素和为sum.
        //这是一个组合问题,并不是一个0-1背包问题，这一点一定要区分开
        //也可以用动态规划解决
        //动态规划五步走的关键点就是：确定dp数组及其下标的含义以及递推公式的推导，这两个点攻下来，基本上就没有什么问题了
        //dp数组及其下标含义：dp[i][j]代表0-i的物品放入容量为j的背包中有几种方法，或者说nums[i]中下标为0-i的元素之和为j有几种组合方法
        vector<vector<int>> dp(nums.size(), vector<int>(sum + 1, 0));
        //递推公式：分两种情况：一种是不放置i号元素，此时只0至i-1号物品，方法有dp[i-1][j]种,第二种是放置i号元素，此时方法有dp[i-1][j-nums[i]]种，所以dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]] (nums[i]<=j)
        
        
        
        //初始化
        //先初始化第一行,只有一个位置百分百置1，其他位置先置0，dp[0][0]可能为1，也可能为2
        if (nums[0] <= sum) dp[0][nums[0]] = 1;
        //再初始化第一列        
        //第一列，如果元素值都不为0的，全部更新为1就可以，如果出现0的话，就不能全为1了
        int numZero = 0;
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] == 0) numZero++;
            dp[i][0] = pow(2, numZero);
        }



        //遍历顺序:自上向下，自左至右
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 1; j <= sum; j++) {
                if (nums[i] <= j) dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
                else dp[i][j] = dp[i - 1][j];
            }
        }
        //举例推导，自己在底下推导就可以
        return dp[nums.size() - 1][sum];
    }
};
方法二：一维dp数组
参考代码随想录的思路独立分析编写
class Solution {
public:
    int findTargetSumWays(vector<int>& nums, int target) {
        //这道题略微复杂，昨天是完全跟着代码随想录的思路来的，今天尝试完全通过自行推导，并简化使用一维dp数组
        //基本思路为bagSize = (sum + target) / 2; 并且bagSize为整数,sum + target一定为偶数
        int sum = 0;
        for(int i:nums) sum += i;
        if ((sum + target) % 2 != 0 || abs(target) > sum) return 0;
        int setSum = (sum + target) / 2;
        //组合问题用动态规划解：
        //1.确定dp数组及其下标的含义：dp[i][j]为0-i号元素放入容量为j的背包中有几种放法
        //2.自行举例推导递推公式：
        //dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i]] nums[i]<=j;
        //dp[i][j] = dp[i-1][j] nums[i] > j;
        //初始化：因为递推公式要用到i - 1,所以i==0时必须初始化，nums[0] = 0时，dp[0][0] = 2(即放入与不放入都可以)，nums[0]!=0时，dp[0][0] = 1(只能不放入)
        //遍历：自左至右，自上向下遍历
        //举例推导：草稿纸自行推导也可以
        //今天尝试用一维dp数组解决该问题，一维数组不过是要重复多为数组的每一行，更新时要用到上一轮更新时的数值
        vector<int> dp(setSum + 1, 0);
        //初始化
        if (nums[0] == 0) dp[0] = 2;
        else {
            dp[0] = 1;
            if (nums[0] <= setSum) dp[nums[0]] = 1;
        }
        //递推公式：dp[j] = dp[j] + dp[j - nums[i]]  nums[i]<=j;
        //          dp[j] = dp[j] nums[i] > j;
        //遍历：自上向下遍历，自右向左遍历
        for (int i = 1; i < nums.size(); i++) {
            for (int j = setSum; j >= nums[i]; j--) {
                dp[j] = dp[j] + dp[j - nums[i]];
            }
        }
        return dp[setSum];
    }
};

10.10日任务：一和零

这道题是0-1背包三维数组版，用来体会0-1背包动态规划没什么问题。

按照代码随想录的思路来，这道题用三维数组理解是最直观的，倘若直接用二维数组讲，需要读者对于0-1背包问题理解的非常彻底。
首先是三维数组版：
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        //不会，直接看代码随想录的思路,这道题还是有点难度的，之前是二维，这次算是三维
        //从三维角度出发是更容易理解这道题目的
        //1.确定dp数组及其下标的含义：dp[i][j][k]表示下标为0-i的字符串放入容量为（j个0,k个1）的背包中的最大价值（每个字符串的价值为1）
        //递推公式：两种情况：1.第i个字符串放不进去，dp[i][j][k] = dp[i-1][j][k];
        //2.第i个字符串能放进去：dp[i][j][k] = value[i]+dp[i-1][j-zeronum][k-onenum];
        //三维递推公式：dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-zeronum][k-onenum]) i>=1,j>=zeronum,k>=onenum
        //三维降到二维的递推公式：dp[j][k] = max(dp[j][k],dp[j-zeronum][k-onenum])
        //三维和二维的代码都要敲
        //先敲三维的
        //初始化：因为三维递推公式有i-1,所以要初始化i-1所在的二维数组
        vector<vector<vector<int>>> dp(strs.size(), vector<vector<int>>(m + 1, vector<int>(n + 1, 0)));
        int zeroNum = 0;
        int oneNum = 0;
        for (char c:strs[0]) {
            if (c == '0') zeroNum++;
            else oneNum++;
        }
        for (int j = 0; j <= m; j++) {
            for (int k = 0; k <= n; k++) {
                if (j >= zeroNum && k >= oneNum) dp[0][j][k] = 1;
            }
        }
        //遍历strs按顺序遍历,再自左至右遍历，自上向下遍历
        for (int i = 1; i < strs.size(); i++) {
            zeroNum = 0;
            oneNum = 0;
            for (char c:strs[i]) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k <= n; k++) {
                    if(j >= zeroNum && k >= oneNum) dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j-zeroNum][k-oneNum] + 1);
                    else dp[i][j][k] = dp[i-1][j][k];
                }
            }
        }
        return dp[strs.size() - 1][m][n];
    }
};
二维数组版：
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        //不会，直接看代码随想录的思路,这道题还是有点难度的，之前是二维，这次算是三维
        //从三维角度出发是更容易理解这道题目的
        //1.确定dp数组及其下标的含义：dp[i][j][k]表示下标为0-i的字符串放入容量为（j个0,k个1）的背包中的最大价值（每个字符串的价值为1）
        //递推公式：两种情况：1.第i个字符串放不进去，dp[i][j][k] = dp[i-1][j][k];
        //2.第i个字符串能放进去：dp[i][j][k] = value[i]+dp[i-1][j-zeronum][k-onenum];
        //三维递推公式：dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-zeronum][k-onenum]) i>=1,j>=zeronum,k>=onenum
        //三维降到二维的递推公式：dp[j][k] = max(dp[j][k],dp[j-zeronum][k-onenum]+1)
        //三维和二维的代码都要敲
        //现在敲二维的
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        //初始化
        //遍历，由于每一轮更新要用到上一轮的所有数据，所以只能从右向左遍历,从下向上遍历
        //初始化和遍历放在一块写好了
        int zeroNum = 0;
        int oneNum = 0;
        for (int i = 0; i < strs.size(); i++) {
            zeroNum = 0;
            oneNum = 0;
            for (char c:strs[i]) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int j = m; j >= zeroNum; j--){
                for (int k = n; k >= oneNum; k--) {
                    dp[j][k] = max(dp[j][k], dp[j-zeroNum][k-oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};

底下这种写法运行速度更快，我不太清楚是什么原因，二刷时专门注意一下
class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        //不会，直接看代码随想录的思路,这道题还是有点难度的，之前是二维，这次算是三维
        //从三维角度出发是更容易理解这道题目的
        //1.确定dp数组及其下标的含义：dp[i][j][k]表示下标为0-i的字符串放入容量为（j个0,k个1）的背包中的最大价值（每个字符串的价值为1）
        //递推公式：两种情况：1.第i个字符串放不进去，dp[i][j][k] = dp[i-1][j][k];
        //2.第i个字符串能放进去：dp[i][j][k] = value[i]+dp[i-1][j-zeronum][k-onenum];
        //三维递推公式：dp[i][j][k] = max(dp[i-1][j][k],dp[i-1][j-zeronum][k-onenum]) i>=1,j>=zeronum,k>=onenum
        //三维降到二维的递推公式：dp[j][k] = max(dp[j][k],dp[j-zeronum][k-onenum]+1)
        //三维和二维的代码都要敲
        //现在敲二维的
        vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
        //初始化
        //遍历，由于每一轮更新要用到上一轮的所有数据，所以只能从右向左遍历,从下向上遍历
        //初始化和遍历放在一块写好了
        for (string str:strs) {
            int zeroNum = 0;
            int oneNum = 0;
            for (char c:str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int j = m; j >= zeroNum; j--){
                for (int k = n; k >= oneNum; k--) {
                    dp[j][k] = max(dp[j][k], dp[j-zeroNum][k-oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};

10.11日任务：完全背包理论基础

从二维向一维理解会更容易理解，直接理解一维的话，需要对背包问题理解非常深入才能达到这个水平。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	//之前是0-1背包问题
	//现在是完全背包问题
	//按照卡码网52：携带研究材料来做
	//首先是解决输入问题
	int N = 0, V = 0;
	cin >> N >> V;
	vector<int> weight(N, 0);
	vector<int> value(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> weight[i] >> value[i];
	}
	//这道题第一下用二维数组还是比较好理解
	//1.确定dp数组及其下标的含义:dp[i][j],表示下标为0-i的物品放入到容量为j的背包中可以达到的最大价值
	//2.递推公式推导：对于d[i][j],分两种情况：
	// 第一种情况：i物品放不进去，dp[i][j] = dp[i-1][j]; j<weight[i]
	// 第二种情况：i物品可以放进去 dp[i][j] = value[i]+dp[i][j-weight[i]]; j>=weight[i]. 这一步是和0-1背包不同的地方，完全背包每个物品都可以放无数次
	//定义dp数组全部初始化为0
	vector<vector<int>> dp(N, vector<int>(V + 1, 0));
	//初始化，修改额外位置即可
	for (int i = 1; i <= V; i++) {
		if (i % weight[0] == 0) dp[0][i] = value[0] * i / weight[0];
	}
	//遍历：正常从左至右，从上至下遍历
	for (int i = 1; i < N; i++) {
		for (int j = 0; j <= V; j++) {
			if (j < weight[i]) dp[i][j] = dp[i - 1][j];
			else dp[i][j] = max(dp[i - 1][j],value[i] + dp[i][j - weight[i]]);
		}
	}
	//举例推导，自行纸上推导即可
	cout << dp[N - 1][V];
	return 0;
}
用一维数组解：（二维的思路理清楚了，一维就顺理成章了，直接上一维还是比较牵强的）
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	//之前是0-1背包问题
	//现在是完全背包问题
	//按照卡码网52：携带研究材料来做
	//首先是解决输入问题
	int N = 0, V = 0;
	cin >> N >> V;
	vector<int> weight(N, 0);
	vector<int> value(N, 0);
	for (int i = 0; i < N; i++) {
		cin >> weight[i] >> value[i];
	}
	//这道题第一下用二维数组还是比较好理解
	//1.确定dp数组及其下标的含义:dp[i][j],表示下标为0-i的物品放入到容量为j的背包中可以达到的最大价值
	//2.递推公式推导：对于d[i][j],分两种情况：
	// 第一种情况：i物品放不进去，dp[i][j] = dp[i-1][j]; j<weight[i]
	// 第二种情况：i物品可以放进去 dp[i][j] = value[i]+dp[i][j-weight[i]]; j>=weight[i]. 这一步是和0-1背包不同的地方，完全背包每个物品都可以放无数次
	
	//定义dp数组全部初始化为0
	vector<int> dp(V + 1, 0);
	//遍历：正常从左至右，从上至下遍历
	for (int i = 0; i < N; i++) {
		for (int j = weight[i]; j <= V; j++) {
			dp[j] = max(dp[j],value[i] + dp[j - weight[i]]);
		}
	}
	//举例推导，自行纸上推导即可
	cout << dp[V];
	return 0;
}

10.12日任务：零钱兑换II

后面的题目综合性比较强，套模板不怎么好套了，需要对于问题彻底理解才能搞定。

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        //类似完全背包问题，但并不完全是，是一种与完全背包问题接近的动态规划
        //1.确定dp数组及其下标含义：dp[i][j]表示0-i物品凑成总重量为j的背包有几种方法
        //2.推导递推公式：dp[i][j] = dp[i - 1][j] + dp[i][j - weight[i]] j>=weight[i]
        //dp[i][j] = dp[i-1][j] j<weight[i]
        //降成一维的话：dp[j] = dp[j] + dp[j-weight[i]] j>=weight[i]
        if (amount == 0) return 1;
        vector<uint64_t> dp(amount + 1, 0);
        //初始化：
        //遍历顺序，自上至下，自左至右
        for (int i = 0; i < coins.size(); i++) {
            for (int j = coins[i]; j <= amount; j++) {
                if (j == coins[i]) dp[j] = dp[j] + 1;
                dp[j] = dp[j] + dp[j - coins[i]];
            }
        }
        //举例推导：自行纸上推导
        return dp[amount];
    }
};

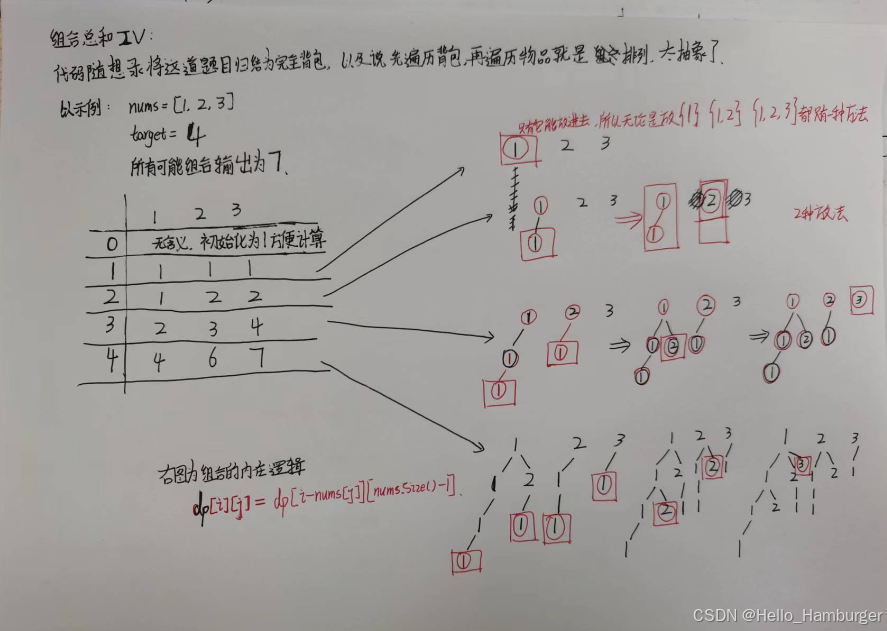
10月12日任务（当日第二题）：组合总和IV

上面一道题为组合问题还是比较好理解，这道题为排列问题，理解难度倍增。

按照自己的理解编写，我的理解会放个图留在下面
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
       //代码随想录的思路跨度太大了，我按照自己的思路来
       //先从二维数组出发会比较好理解
       //dp[i][j]代表容量为i的背包，放置下标为0-j的物品，有几种放法（排列放法，不是组合放法）
       //先遍历物品再遍历背包是组合放法，先遍历背包再遍历物品为排列放法（需要多次刷题体会）
       //递推公式 
       //dp[i][j] = dp[i][j-1] + dp[i-nums[j]][nums.size() - 1]; (i>=nums[j],j>=1)
       //dp[i][j] = dp[i-nums[j]][nums.size() - 1]; (j==0,i>=nums[j])
       //dp[i][j] = dp[i][j-1] i<nums[j]
       vector<vector<uint32_t>> dp(target + 1, vector<uint32_t>(nums.size(), 0));
       //初始化
       for (int i = 0; i < nums.size(); i++) dp[0][i] = 1;
       //遍历顺序：先遍历背包再遍历物品
       for (int i = 1; i <= target; i++) {
            for (int j = 0; j < nums.size(); j++) {
                if (i >= nums[j]) {
                    if (j == 0) {
                        dp[i][j] = dp[i-nums[j]][nums.size() - 1];
                    }
                    else dp[i][j] = dp[i][j-1] + dp[i-nums[j]][nums.size() - 1];
                }
                else {
                    if (j == 0) dp[i][j] = 0;
                    else dp[i][j] = dp[i][j - 1];
                }
                
            }
       }
       return dp[target][nums.size() - 1];
    }
};
再从我的二维数组法降低到一维数组法就可以更好理解了
class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
       //代码随想录的思路跨度太大了，我按照自己的思路来
       //先从二维数组出发会比较好理解
       //dp[i][j]代表容量为i的背包，放置下标为0-j的物品，有几种放法（排列放法，不是组合放法）
       //先遍历物品再遍历背包是组合放法，先遍历背包再遍历物品为排列放法（需要多次刷题体会）
       //递推公式 
       //dp[i][j] = dp[i][j-1] + dp[i-nums[j]][nums.size() - 1]; (i>=nums[j],j>=1)
       //dp[i][j] = dp[i-nums[j]][nums.size() - 1]; (j==0,i>=nums[j])
       //dp[i][j] = dp[i][j-1] i<nums[j]
       //降到一维数组去
       //dp数组及其下标含义：dp[i]表示装满用下标为0-j装满容量为i的背包有几种放法，排列放法
       vector<uint32_t> dp(target + 1, 0);
       //初始化
       dp[0] = 1;
       //遍历:先遍历背包再遍历物品
       for (int i = 1; i <= target; i++) {
        for (int j = 0; j < nums.size(); j++) {
            if (nums[j] <= i) dp[i] = dp[i] + dp[i - nums[j]];
        }
       }
       return dp[target];
    }
};

遍历每一行都是在前面的基础上做添加，这个问题并不是特别好理解，后面多刷刷题就能理解的更深一些。

10月13日任务：爬楼梯（进阶版）

和昨天的排列问题一模一样，一遍过，没什么难度。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	//可以确定：这个和昨天的题目一样是一个排列问题
	//1.确定dp数组及其下标含义：dp[i]爬上i阶共有几种方法
	//2.递推公式：
	//dp[i] = dp[i] + dp[i - nums[j]] i>=nums[j]
	//3.初始化
	int n, m;
	cin >> n >> m;
	vector<int> dp(n + 1, 0);
	dp[0] = 1;
	//遍历顺序：先遍历背包再遍历物品
	for (int i = 1; i <= n; i++) {
		for (int j = 0; j < m; j++) {
			if ((j + 1) <= i) dp[i] += dp[i - (j + 1)];
		}
	}
	cout << dp[n];
	return 0;
}

10.13日任务（当日第二题）：零钱兑换

这道题是组合问题，不过对于其中-1的处理，是需要对dp数组的含义以及具体意义有很深的把握才能做出来。
推导递推公式时，在草稿纸上填写dp数组的时候尽量全部填写完毕，因为仅仅填写一部分的话可能会疏忽掉一些特殊情况，这个问题到后面比较浪费时间去查找。
对，重点：推导递推公式时，在草稿纸上填写dp数组的时候尽量全部填写完毕

按照自己的思路独立编写
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //这题目是难易交替,确实,一直一个套路也确实太无趣了
        //这道题我觉得是一个组合问题
        //1.确定dp数组及其下标含义：dp[i][j],下标为0-i的物品，刚好装进容量为i的背包最少硬币个数
        //2.递推公式 dp[i][j] = min(dp[i - 1][j],1 + dp[i][j-nums[i]]) (nums[i] <= j)(能放进去)
        //放不进去：dp[i][j] = dp[i - 1][j];
        //降到2维：dp[j] = min(dp[j],1+dp[j-nums[i]])
        //初始化
        if (amount == 0) return 0;
        vector<int> dp(amount + 1, 0);
        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            if (i % coins[0] == 0) dp[i] = i / coins[0];
            else dp[i] = -1;
        }
        //遍历顺序：先遍历物品，再遍历背包（自大向小遍历）
        for (int i = 1; i < coins.size(); i++) {
            for (int j = coins[i]; j <= amount; j++) {
                if (dp[j-coins[i]] != -1 && dp[j] != -1) dp[j] = min(dp[j], 1 + dp[j - coins[i]]);
                else if (dp[j-coins[i]] != -1 && dp[j] == -1) dp[j] = 1 + dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};
代码随想录的思路更加简便，本质上就是对于-1这个情况的考虑有没有考虑到
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //这题目是难易交替,确实,一直一个套路也确实太无趣了
        //这道题我觉得是一个组合问题
        //1.确定dp数组及其下标含义：dp[i][j],下标为0-i的物品，刚好装进容量为i的背包最少硬币个数
        //2.递推公式 dp[i][j] = min(dp[i - 1][j],1 + dp[i][j-nums[i]]) (nums[i] <= j)(能放进去)
        //放不进去：dp[i][j] = dp[i - 1][j];
        //降到2维：dp[j] = min(dp[j],1+dp[j-nums[i]])
        //初始化
        vector<int> dp(amount + 1, INT_MAX);
        dp[0] = 0;
        //遍历顺序：先遍历物品，再遍历背包（自大向小遍历）
        for (int i = 0; i < coins.size(); i++) {
            for (int j = coins[i]; j <= amount; j++) {
                if (dp[j-coins[i]] != INT_MAX) dp[j] = min(dp[j], 1 + dp[j - coins[i]]);
            }
        }
        if (dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

10.13日感悟：代码随想录给的思路太简洁了，自己在做题的时候一定要把dp数组扎扎实实推导填写一遍，这样才能对题目有更深的理解，编写的代码一开始必然是跟随自己的思路但是并不是最简写法。重要的是代码一定要体现自己的思路和想法，最简代码可以在这个基础上再调整。不要图快，要扎扎实实，实事求是。

10.14日任务：完全平方数

比较简单，按照完全背包的思路就顺利通过了。
class Solution {
public:
    int numSquares(int n) {
        //1.确定dp数组及其下标的含义 ：dp[i]表示和为n的完全平方数的最少数量
        //递推公式：dp[j] = min(dp[j],1+dp[j - nums[i]]) (nums[i] <= j)
        //初始化
        //遍历顺序：自上向下，自左至右
        int k = 0;
        while (k * k <= n) {
            k++;
        }
        if ((k - 1) * (k - 1) == n) return 1;
        vector<int> dp(n + 1, INT_MAX);
        dp[0] = 0;
        for(int i = 1; i <= k-1; i++) {
            for (int j = i * i; j <= n; j++) {
                dp[j] = min(dp[j], 1 + dp[j - i * i]);
            }
        }
        return dp[n];
    } 
};

10.14日任务（当日第二题）：单词拆分

思路和代码随想录的一样，题目并不好想，比较烧脑，掌握动态规划完全背包的思路就可以了，没必要纠结这些复杂难想的题目。

这道题其实并不好理解，细节方面用背包来讲比较牵强，并不是一个很好想的题目，二刷可以来加深一下印象。
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        //看到这道题应该立马想到的是先遍历背包，再遍历物品的遍历方式
        //1.确定dp数组及其下标含义：dp[i]为wordDict中的单词是否可以构成字符串s中的0-i的字符
        //递推公式：倘若dp[j] = 1,j < i,当wordDict中有字符串为s的[j,i]部分的话，那么dp[i] = 1
        //初始化dp[0] = true;
        unordered_set wordSet(wordDict.begin(), wordDict.end());
        vector<bool> dp(s.size() + 1, false);
        dp[0] = true;
        //遍历顺序，先遍历背包，再遍历物品
        //此时背包和物品的表示还比较抽象
        for (int i = 1; i <= s.size(); i++) { //先遍历背包
            for (int j = 0; j < i; j++) { //再遍历物品
                string word = s.substr(j, i-j);//也是个左闭右开
                if (wordSet.find(word) != wordSet.end() && dp[j]) {
                    dp[i] = true;
                }  
            }
        }
        return dp[s.size()];
    }
};

10.15日任务：多重背包理论基础

0-1背包问题的拓展，很简单，没什么难度，一遍过。
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int main() {
	//多重背包问题：本质上是0-1问题的翻版，物品有N种，重量为w[i],价值为v[i],每种物品数量有k[i]个可用，背包容量为C
	//0-1背包问题：和多重背包问题的区别就是k[i]均为1
	//把多重背包问题铺开，就变成0-1背包了
	//先解决输入：
	int C, N;
	cin >> C >> N;
	vector<int> w(N, 0);
	vector<int> v(N, 0);
	vector<int> k(N, 0);
	for (int i = 0; i < N; i++) cin >> w[i];
	for (int i = 0; i < N; i++) cin >> v[i];
	for (int i = 0; i < N; i++) cin >> k[i];
	//1.dp数组及其下标含义：dp[j] 表示下标为0-i的物品放进容量为j的背包中最多能放多少价值
	//2.递推公式：dp[j] = max(dp[j],k[i] + dp[j - w[i]]) w[i] <= j;
	//初始化:不用特别初始化直接放进去用就行
	//遍历顺序，自上向下，自右向左
	vector<int> dp(C + 1, 0);
	for (int i = 0; i < N; i++) {
		for (int m = 0; m < k[i]; m++) {
			for (int j = C; j >= w[i]; j--) {
				dp[j] = max(dp[j], v[i] + dp[j - w[i]]);
			}
		}
	}
	cout << dp[C];
	return 0;
}

10月15日（当日第二题）：打家劫舍

很基础的动态规划问题。

class Solution {
public:
    int rob(vector<int>& nums) {
        //按照常规思路走就行
        //1.dp数组及其下标含义：dp[i] 代表0-i号房屋最多能偷盗的金额
        //2.递推公式：第一种情况：不偷，dp[i] = dp[i - 1];
        //第二种情况： 偷： dp[i] = dp[i-2] + nums[i]
        //dp[i] = max(dp[i-1], nums[i] + dp[i - 2]);
        //初始化
        vector<int> dp(nums.size());
        if (nums.size() == 1) return nums[0];
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for (int i = 2; i < nums.size(); i++) {
            dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        }
        return dp[nums.size() - 1];
    }
};

10月15日任务（当日第三题）：打家劫舍II

按照代码随想录的思路来，相对比较简单

class Solution {
public:
    int rob(vector<int>& nums) {
        //按照代码随想录的思路：考虑两种情况：
        //只关注下标为0到i-2的房屋
        //只关注下标为1到i-1的房屋
        vector<int> dp1(nums.size() - 1);
        vector<int> dp2(nums.size());
        if (nums.size() == 1) return nums[0];
        if (nums.size() == 2) return max(nums[0],nums[1]);
        dp1[0] = nums[0];
        dp1[1] = max(nums[0], nums[1]);
        dp2[0] = nums[0];
        dp2[1] = nums[1];
        dp2[2] = max(nums[1], nums[2]);
        for (int i = 2; i < nums.size() - 1; i++) {
            dp1[i] = max(dp1[i - 1], dp1[i - 2] + nums[i]);
            dp2[i + 1] = max(dp2[i], dp2[i - 1] + nums[i + 1]);
        }
        return max(dp1[nums.size() - 2], dp2[nums.size() - 1]);
    }
};

10.16日任务：打家劫舍III

二叉树和动态规划的结合

class Solution {
public:
    //1.dp数组的含义vector<int>(2),一个是不偷该房屋最大抢到的钱，一个是偷该房屋最大抢到的钱
    vector<int> robTree(TreeNode* root) {
        //终止条件
        if (root == nullptr) return vector<int>{0,0};
        //顺序执行
        //先不考虑当前节点，即考虑左侧节点
        vector<int> left = robTree(root->left);
        //考虑右侧节点
        vector<int> right = robTree(root->right);
        //偷当前的
        int val1 = root->val + left[0] + right[0];
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2,val1};  
    }
    int rob(TreeNode* root) {
        //结合了二叉树，目前自己的刷题进度比较快，前面知识点忘得比较多，慢慢来，别给自己压力
        //之前进度太慢了，现在尝试进行节约时间，如果有之前的代码模板，直接拿过来用，重点在思路，而不是一直刷手感，重敲相同的代码太浪费时间了
        //直接按照代码随想录的思路来：这道题是二叉树和dp数组的结合，或者说递归和动态规划的结合
        vector<int> result = robTree(root);
        return max(result[0], result[1]);
    }
};

10月17日-10.20日任务：

下面的几道股票问题值得多多品味。

任务一：买卖股票的最佳时机

值得反复回味体会。简单来讲：dp数组是prices.size()行2列。第一列决定哪一天买入，那自然
是最便宜的那一天，第二列决定哪一天卖出，自然是dp[i-1][0] + prices[i]最大的那一天。同
时dp[0][1]初始化为0，则保证了当最终赔本时，输出为0.输出在dp[prices.size() - 1][1]. 这下这道题算是整明白了。
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //I Love You
        //我自己的思路闭塞了，按照代码随想录的思路来
        //代码随想录给出的是多种方法，因为这里是再第一遍学动态规划，所以就按照动态规划的方法来，其他方法二刷的时候来搞
        //1.dp数组及其下标的含义
        //dp[i][0]表示第i天持有股票所得的最多现金，dp[i][1]则表示第i天不持有股票所得的最多现金
        //2.递推公式：
        //dp[i][0] = max(dp[i-1][0], -price[i]);//1.昨天持有2.昨天不持有，这道题只有一次买入卖出机会，所有昨天要么持有，要么现金为0
        //dp[i][1] = max(dp[i-1][1], dp[i-1][0] + price[i])//1.昨天不持有，昨天持有
        vector<vector<int>> dp(prices.size(), vector<int>(2, 0));
        //已经全部初始化为0
        dp[0][0] = -prices[0];
        //遍历顺序，从头至尾
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i-1][0], -prices[i]);
            dp[i][1] = max(dp[i-1][0] + prices[i], dp[i-1][1]);
        }
        return dp[prices.size() - 1][1];
    }
};

任务二:买卖股票的最佳时机II

需要反复体会，并不是自己想象的那么简单。

任务一中，只能倒腾一支股票，任务二则能够连续不断的倒腾股票，值得反复体会。
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //和上一道题只有递推公式有区别
        vector<vector<int>> dp(prices.size(), vector<int>(2));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }        
        return dp[prices.size() - 1][1];
    }
};

任务三：买卖股票的最佳时机III

还得二刷品味，第一遍更像是背了一遍题目，但是对于整个过程递推过程的理解并不深入，还需要在细细体会。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //先包含特殊情况
        if (prices.size() == 1) return 0;
        //限定最大两笔交易
        //按照代码随想录的思路：默认可以当日买入卖出
        //1.dp数组及其下标含义;dp[i][0]不操作，dp[i][1]:第一次交易中持有股票；dp[i][2]:第一次交易中卖出股票
        //dp[i][3]第一次交易结束后，第二次持有股票，dp[i][4]第二次卖出股票
        vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
        //明确可以当日买进卖出
        //初始化:默认可以当日买进卖出
        dp[0][0] = 0;//不做任何操作
        dp[0][1] = -prices[0];//第一天第一次买入
        dp[0][2] = 0;//第一天第一次卖出
        dp[0][3] = -prices[0];//第一天第二次买入
        dp[0][4] = 0;//第一天第二次卖出
        for (int i = 1; i < prices.size(); i++) {
            //第i天第一次持有情况:1.要么延续持有 2.要么第一次买入
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
            //第i天第一次未持有情况:1.要么延续未持有 2.要么卖出
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
            //第i天第二次持有情况：dp[i][2]既可以理解为在不同的时间完成了买入卖出，也可以理解为在同一天完成了买入卖出
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
            //第i天第二次为持有情况：
            dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
        }
        return dp[prices.size() - 1][4];
    }
};

任务四：买卖股票的最佳时机IV

和上一道题一个逻辑，这几道题是需要二刷三刷去细细体会的，不然就只能是背题。

class Solution {
public:
    int maxProfit(int k, vector<int>& prices) {
        //上一次限定两次买卖，这一次限定k次买卖
        //本以为代码随想录要上一个比较高级的方法，结果的确是和上一题两次买卖是一个方法
        vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
        //初始化
        for (int j = 0; j < k; j++) {
            dp[0][2 * j + 1] = -prices[0];
        }
        //遍历：自前向后遍历,prices遍历在外层，k遍历在内层
        for (int i = 1; i < prices.size(); i++) {
            for (int j = 0; j < k; j++) {
                //第i天第j次持有
                dp[i][2 * j + 1] = max(dp[i - 1][2 * j + 1], dp[i - 1][2 * j] - prices[i]);
                dp[i][2 * j + 2] = max(dp[i - 1][2 * j + 2], dp[i - 1][2 * j + 1] + prices[i]);
            }
        }
        return dp[prices.size() - 1][2 * k];
    }
};

10月21日至10月22日任务：

任务一：最佳买卖股票时机含冷冻期

这道题我的思路和代码随想录的思路是不一致的，我是按照买卖股票的顺序来的，先持有股票，
再卖出股票，再冷冻期，再保持卖出股票这样分成四个状态，我觉得这种思路要比代码随想录的
思路更好。（冷冻期和今天卖出股票两个状态是可以合并的），这道题要细细体会，没有想象中那么简单。
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        //题目比较复杂，先看代码随想录的思路，再试着跟着代码随想录的思路走一走看看
        //1.确定dp数组及其下标含义
        //分为四种情况：按顺序来：1.持有股票dp[i][0];2.今天卖出股票dp[i][1]3.今天是冷冻期dp[i][2],4.今天是保持卖出dp[i][3]
        //递推公式： dp[i][0] = max(max(dp[i-1][0],dp[i-1][2] - prices[i]),dp[i-1][3] - prices[i]);
        //dp[i][1] = dp[i-1][0] + prices[i];
        //dp[i][2] = dp[i-1][1];
        //dp[i][3] = dp[i-1][3];
        //初始化
        vector<vector<int>> dp(prices.size(), vector<int>(4, 0));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        dp[0][2] = 0;
        dp[0][3] = 0;
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(max(dp[i-1][0], dp[i-1][2] - prices[i]), dp[i-1][3] - prices[i]);
            dp[i][1] = dp[i-1][0] + prices[i];
            dp[i][2] = dp[i-1][1];
            dp[i][3] = max(dp[i-1][3],dp[i-1][2]);
        }
        return max(dp[prices.size() - 1][1],max(dp[prices.size() - 1][2],dp[prices.size() - 1][3]));
    }
};

任务二：买卖股票的最佳时机含手续费

这个就比较简单了
class Solution {
public:
    int maxProfit(vector<int>& prices, int fee) {
        //加手续费有点简单了吧
        vector<vector<int>> dp(prices.size(), vector<int>(2));
        dp[0][0] = -prices[0];
        dp[0][1] = 0;//第一天必然是不操作卖出，还得出手续费呢
        for (int i = 1; i < prices.size(); i++) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = max(dp[i - 1][1],dp[i - 1][0] + prices[i] - fee);
        }
        return dp[prices.size() - 1][1];
    }
};

任务三：最长递增子序列

为什么要用result,这是因为dp[i]表示的是：在nums中,以nums[i]为最大元素的最大严格递增子序列的长度，然而nums中的最大严格递增子序列不一定包含nums[i],关于result的理解，画图就好了，参考输入：nums =[1,3,6,7,9,4,10,5,6]，在这种情况下，就会发现必须用result.
class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        //1.确定dp数组及其下标含义：dp[i]为下标为0-i的元素中最长严格递增子序列的长度,且这个子序列的最大值为nums[i]
        //递推公式：
        //初始化：全部初始化为1
        vector<int> dp(nums.size(), 1);
        int result = 1;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1); //dp[j]代表前0-j个元素中的最长严格递增子序列的长度
            }
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

10月23日任务：

任务一：最长连续递增子序列

确实比较简单，轻松一遍过
class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        //dp数组及其下标的含义：dp[i]为0-i元素中最长连续递增子序列，且该子序列必须包含下标为i的元素
        //dp[i] = dp[i-1]+1;nums[i]>nums[i-1];
        //dp[i] = 1;nums[i]<=nums[i-1];
        //初始化
        if (nums.size() == 1) return 1;
        vector<int> dp(nums.size(), 1);
        dp[0] = 1;
        int result = 1;
        //遍历顺序    
        for (int i = 1; i < nums.size(); i++) {
            if (nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;
            if (dp[i] > result) result = dp[i];
        }
        return result;
        //自行推导
    }
};

任务二：最长重复子数组

参考代码随想录的思想，再按自己的思路来，值得反复推敲，不推敲反复验证，就是在背题。值
得二刷反复看。
class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        //这两天遇到的题目略显复杂，看解析思路也得半天，没法很快触及本质。
        //我的方法就是先看一遍解析，然后尝试自己推导整个流程
        //按照代码随想录的思路来
        //1.确定dp数组及其下标的含义dp[i][j]:nums1中下标为0-i的元素和nums2中下标为0-j的元素，这两个短数组中公共的长度最长的子数组的长度,这个公共子数组的结尾为nums1[i],nums2[j]
        //递推公式：dp[i][j] = dp[i-1][j-1]+1
        //初始化
        vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));
        //需要初始化第一行和第一列：
        int result = 0;
        for (int i = 0; i < nums2.size(); i++) if(nums2[i] == nums1[0]) {dp[0][i] = 1; result = 1;}
        for (int i = 1; i < nums1.size(); i++) if (nums1[i] == nums2[0]) {dp[i][0] = 1; result = 1;}
        //遍历
        for (int i = 1; i < nums1.size(); i++) {
            for (int j = 1; j < nums2.size(); j++) {
                if (nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
                if (dp[i][j] > result) result = dp[i][j];
            }
        }        
        return result;
    }
};

任务三：最长公共子序列

没怎么搞明白，二刷再继续。

题目并不好理解，动态规划本身没有难度，有难度的是对问题的理解。得二刷，一刷我没有完全
理解。理解的重点就是要自己画表格推导递推公式，这个推明白了，问题也就解决了。
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        //按照代码随想录的思路来
        //dp数组及其下标含义：dp[i][j]表示text1中0-i号元素与text2中0-j号元素，两个数组之间最大公共子序列的长度
        //dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
        //dp[i][j] = dp[i-1][j-1] + 1;
        vector<vector<int>> dp(text1.size(), vector<int>(text2.size(), 0));
        //初始化
        int m = 0;
        while (text1[0] != text2[m] && m < text2.size()) m++;
        for (int i = m; i < text2.size(); i++) dp[0][i] = 1;
        m =0;
        while (text1[m] != text2[0] && m < text1.size()) m++;
        for (int i = m; i < text1.size(); i++) dp[i][0] = 1;
        //遍历
        for (int i = 1; i < text1.size(); i++) {
            for (int j = 1; j < text2.size(); j++) {
                if (text1[i] == text2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        } 
        return dp[text1.size() - 1][text2.size() - 1];
    }
};

10月24日任务：

任务一：不相交的线

二刷再不会的话就直接和AI问答battle.

和上一道题一模一样，但是这个逻辑我没有看懂。
class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        //和上一道题公共子序列是一个问题
        vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));
        //初始化
        int m = 0;
        while (m < nums2.size() && nums1[0] != nums2[m]) m++;
        for (int i = m; i < nums2.size(); i++) dp[0][i] = 1;
        m =0;
        while (m < nums1.size() && nums1[m] != nums2[0]) m++;
        for (int i = m; i < nums1.size(); i++) dp[i][0] = 1;
        //遍历
        for (int i = 1; i < nums1.size(); i++) {
            for (int j = 1; j < nums2.size(); j++) {
                if (nums1[i] == nums2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        } 
        return dp[nums1.size() - 1][nums2.size() - 1];
    }
};

10.25日任务：

任务一：最大子序和

本质上：当几个数的和为负数时，就可以和下一个元素分开了，如果和始终为正数，那么需要记录正数出现的最大值。

本质上：当几个数的和为负数时，就可以和下一个元素分开了，如果和始终为正数，那么需要记录正数出现的最大值。
这道题的难点在于dp数组的含义，dp[i]的值对应的是包含下标为i的元素的连续子数组的最大和，如果不包含下标为i的元素，那么dp[i+1]只能重新计算（因为与前面不连贯构不成连续子数组了），只有包含下标为i的元素，dp[i - 1] + nums[i]才有意义。
class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        //动态规划不是问题，问题是如何把问题和动态规划结合起来，需要花时间，面试得考虑背题
        //dp数组及其下标含义：dp[i]表示0-i中包含i的子数组中和最大的子数组
        //dp[i] = max(nums[i], dp[i - 1] + nums[i]);
        vector<int> dp(nums.size(), 0);
        dp[0] = nums[0];
        int result = nums[0];
        for (int i = 1; i < nums.size(); i++) {
        	//倘若dp[i-1]<0,那么就没必要继续加了，直接从头计算
            dp[i] = max(dp[i - 1] + nums[i], nums[i]);
            if (dp[i] > result) result = dp[i];
        }
        return result;
    }
};

任务二：判断子序列

和判断最长公共子序列是一个问题。
之前不理解的点是dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
现在明白了，画图在底下了。
class Solution {
public:
    bool isSubsequence(string s, string t) {
        //和判断最长公共子序列是一个问题，这个问题我到现在还不是很理解
        //dp数组及其下标含义：dp[i][j]为s的0到i-1元素组成的字符串和t的0-j-1号字符串的最长公共子序列
        //递推公式if(nums[i] == nums[j]) dp[i][j] = dp[i-1][j-1] + 1;
        //if(nums[i] != nums[j]) dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i-1] == t[j-1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return s.size() == dp[s.size()][t.size()];
    }
};

二刷再理解一下，确实比较难理解。

任务三：不同的子序列

这是一道比较困难的题目，被我搞定了，我实在是太棒了
class Solution {
public:
    bool isSubsequence(string s, string t) {
        //和判断最长公共子序列是一个问题，这个问题我到现在还不是很理解
        //dp数组及其下标含义：dp[i][j]为s的0到i-1元素组成的字符串和t的0-j-1号字符串的最长公共子序列
        //递推公式if(nums[i] == nums[j]) dp[i][j] = dp[i-1][j-1] + 1;
        //if(nums[i] != nums[j]) dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
        vector<vector<long>> dp(s.size() + 1, vector<long>(t.size() + 1, 0));
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i-1] == t[j-1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
            }
        }
        return s.size() == dp[s.size()][t.size()];
    }
};

二刷再加深理解。

10.26日任务：

任务一：两个字符串的删除操作

这题太捞了，就是找到两个字符串的公共子序列的长度，然后用两个字符串长度之和减去2倍的公共字符串的长度。
class Solution {
public:
    int minDistance(string word1, string word2) {
        //这题太捞了，就是找到两个字符串的公共子序列的长度，然后用两个字符串长度和减去2倍的公共字符串的长度
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 1; i <= word1.size(); i++) {
            for (int j =1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()];
    }
};

任务二：编辑距离

自己花了1个小时左右解决。
题目还是比较难想的，二刷再加深印象。
class Solution {
public:
    int minDistance(string word1, string word2) {
        //dp数组及其下标含义：dp[i][j]为word1中下标为0到i的字符串转换成word2中第0-j个元素字符串所使用的最小操作数
        //递推公式：
        //if (word1[i] == word2[j]) dp[i][j] = dp[i - 1][j -1];理解为两个字符串末尾元素相等，只需要考虑前面字符串的转换操作数即可
        //if (word1[i] != word2[j]) 情况1：dp[i][j] = dp[i-1][j-1]+1;(末尾元素直接替换)
        //情况二：dp[i][j] = dp[i][j-1]+1;(末尾元素插入)
        //情况三：dp[i][j] = dp[i-1][j]+1;(末尾元素删除)
        //三种情况选择操作数最小的
        if (word1.size() == 0) return word2.size();
        if (word2.size() == 0) return word1.size();
        vector<vector<int>> dp(word1.size(), vector<int>(word2.size(), 0));
        //初始化
        //初始化第一行
        if (word1[0] != word2[0]) dp[0][0] = 1;
        for (int i = 1; i < word2.size(); i++) {
            if (word1[0] == word2[i]) dp[0][i] = i;
            else dp[0][i] = min(i + 1, dp[0][i - 1] + 1);
        }
        //初始化第一列
        for (int i = 1; i < word1.size();i++) {
            if (word1[i] == word2[0]) dp[i][0] = i;
            else dp[i][0] = min(i + 1, dp[i - 1][0] + 1);
        }
        //遍历
        for (int i = 1; i < word1.size(); i++) {
            for (int j =1; j < word2.size(); j++) {
                if (word1[i] == word2[j]) dp[i][j]= dp[i - 1][j -1];
                else dp[i][j] = min(dp[i-1][j-1]+1, min(dp[i][j-1]+1, dp[i-1][j]+1));
            }
        }
        return dp[word1.size() - 1][word2.size() - 1];
    }
};

第三道：回文子串

二刷值得回味，尤其是这种遍历方式在纸上画出来会特别容易理解。
class Solution {
public:
    int countSubstrings(string s) {
        //按照代码随想录的思路来：
        //回文字符串可以通过两端一层一层的剥开，拨开过程中两端的字符一定是相等的。
        //dp数组及其下标含义：dp[i][j]为s中的下标为i到j的字符串是否为回文子串的标志True or False
        //递推公式： if i==j 或者 i+1 == j只要s[i]==s[j]则标记为T
        //if (s[i] == s[j]) j-i>=2,那么dp[i][j] = dp[i+1][j-1](左下角)
        //又根据题意：j>=i,整个矩阵的左下半部分是没用的
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        //遍历顺序:考虑更新过程汇总要用到左下角的元素
        //根据代码随想录的思路：从下往上遍历，从左至右遍历
        int result = 0;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] != s[j]) dp[i][j] = false;
                else {
                    if (j - i <= 1) {dp[i][j] = true; result++;}
                    else if (dp[i + 1][j - 1] == true) {
                        dp[i][j] = true; result++;
                    }
                }
            }
        }
        return result;
    }
};

第四道：最长回文子序列

重中之重，dp数组的含义很重要。

根据代码随想录的思路来：
class Solution {
public:
    int longestPalindromeSubseq(string s) {
        //按照代码随想录的思路来：
        //dp[i][j]代表下标为i-j的字符串中最长的回文子序列
        //递推公式：s[i] == s[j] dp[i][j] = dp[i+1][j-1] + 2;
        //s[i] != s[j] 情况一：dp[i][j] = dp[i][j-1](直接取i到j-1); 情况二：dp[i][j] = dp[i+1][j](直接取i+1到j元素)，两者选最小
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        //初始化：把对角线设置为1，把递推数组画出来就知道为什么了
        for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
        //遍历顺序：自下向上，自左至右，因为要考虑到dp[i+1][j-1],dp[i+1][j],dp[i][j-1]在纸上画一画就明白了
        for (int i = s.size() - 2; i >= 0; i--) {
            for (int j = i + 1; j < s.size(); j++) {
                if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;
                else dp[i][j] = max(dp[i][j - 1],dp[i + 1][j]);
            }
        }
        return dp[0][s.size() - 1];
    }
};

动态规划总结

1.dp数组及其下标的含义非常重要
2.关键在于将问题本身与dp数组结合起来
3.动手画dp数组非常重要。