记忆化搜索：329. 矩阵中的最长递增路径

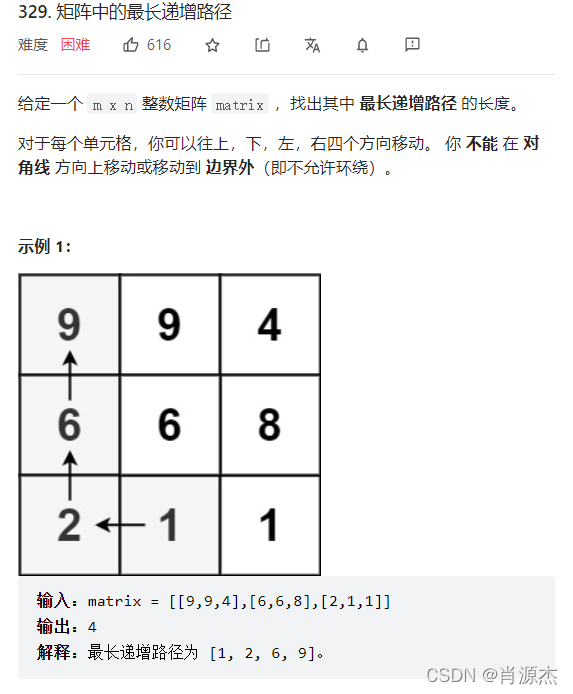
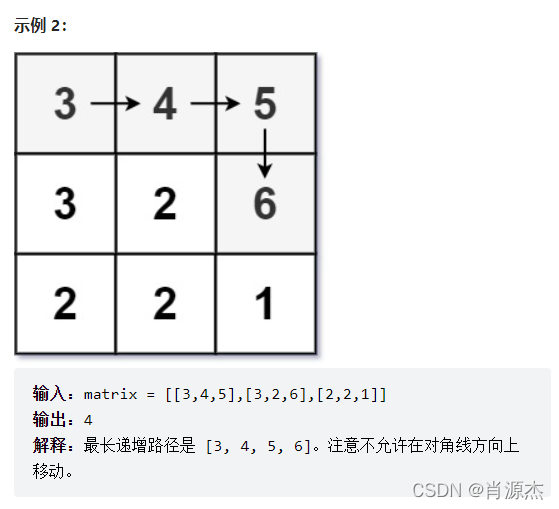
创建一个二维数组f，遍历一遍原二维数组，往四个方向移动，递归，比较记录四个方向上可以获得的最大值将之记录在f[i][j]里，这样，在遍历的过程中，如果f[i][j]已经有值，则返回该值，最后的时间复杂度为O(n)，空间复杂度也为O(n)

code

class Solution {
public:
vector<vector<int>> matrix, f;
int n, m;
const int delta[4][2] = {{1, 0},{-1, 0},{0, 1},{0, -1}};
    int dfs(int i, int j) {
        if (f[i][j]) return f[i][j];
        int ans = 1;
        for (int k = 0; k < 4; k++) {
            int x = delta[k][0] + i, y = delta[k][1] + j;
            if (x >= 0 && x < n && y >= 0 && y < m && matrix[x][y] > matrix[i][j]) ans = max(ans,1 + dfs(x,y));
        }
        f[i][j] = ans;
        return ans;
    }

    int longestIncreasingPath(vector<vector<int>>& _matrix) {
        matrix = _matrix;
        n = matrix.size();
        m = matrix[0].size();
        int res = 0;
        f = vector<vector<int>> (n, vector<int> (m, 0));
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                res = max(res, dfs(i, j));
            }
        }
        return res;
    }
};

此题和分糖果类似