HDU2018 母牛的故事

最新推荐文章于 2024-04-23 17:25:27 发布

原创最新推荐文章于 2024-04-23 17:25:27 发布 · 216 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#HDU #水题

HDU 专栏收录该内容

34 篇文章

订阅专栏

本文探讨了一种类似斐波那契数列的数列计算方法，通过递归与递推两种方式实现。递归方法直接依据数学定义进行深度优先搜索，而递推方法则利用数组存储已计算值，避免重复计算，提高效率。

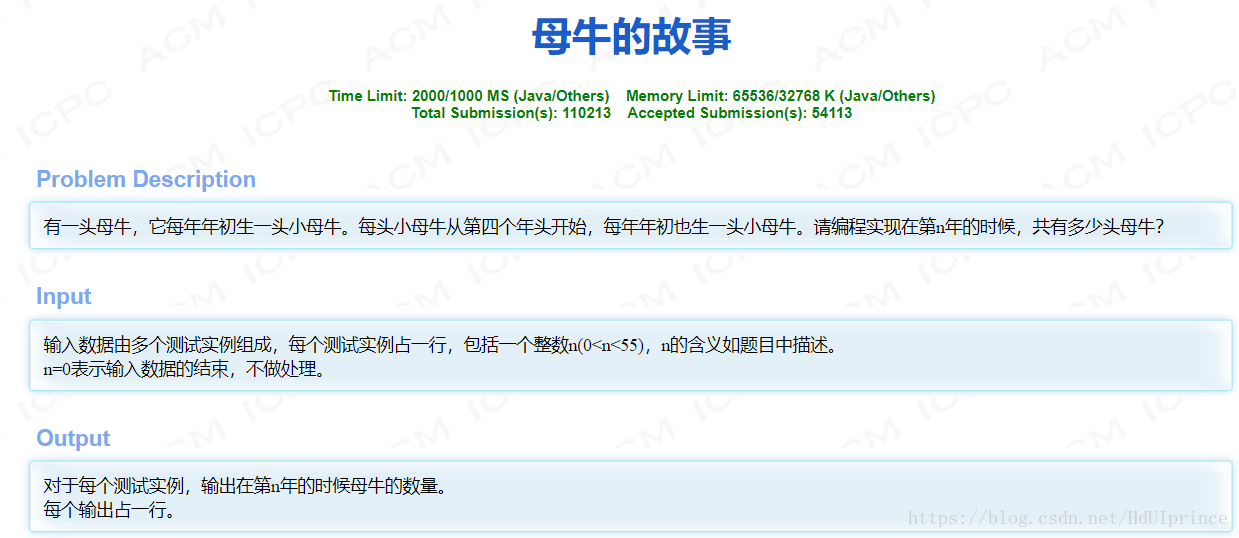
在这里插入图片描述

类似于斐波那契数列。
递推式:
f(n) = n (n<=4)
f(n) = f(n-1) + f(n-3) (n>4)

递归解决：

#include <iostream>
using namespace std;

int sum(int n)
{
	if(n<=4)
	{
		return n;
	}
	else
	{
		return sum(n-1)+sum(n-3);
	}
}

int main()
{
	int n;
	while(cin>>n && n!=0)
	{
		cout << sum(n) << endl;
	}
	return 0;
}

递推解决

#include <iostream>
#include <cstring>
using namespace std;

int main()
{
	int f[60] = {0};
	for(int i=1; i<=4; i++)
	{
		f[i] = i;
	}
	for(int i=5; i<60; i++)
	{
		f[i] = f[i-1] + f[i-3];
	}

	int n;
	while(cin>>n && n!=0)
	{
		cout << f[n] << endl;
	}
	return 0;
}