Notes
文章是关于解耦特征表示的,网络主体基于 auto encoder,但将 encoder 拆成两个: E n c s Enc_s Encs 和 E n c z Enc_z Encz,意图将 latent code 分成两部分:z’=(s, z),其中 s 编码同 label 相关的信息,z 编码其它信息。
实现解耦的思路是靠两个分类器:
- C l f s Clf_s Clfs:对 s 分类,约束 s 捕捉 label 信息;
- C l f z Clf_z Clfz:同 E n c z Enc_z Encz 做对抗学习, C l f z Clf_z Clfz 希望对 z 分类正确,而 E n c z Enc_z Encz 希望编码出的 z 使 C l f z Clf_z Clfz 分类错误(单标签下输出的概率向量全是 1 N c l a s s \frac{1}{N_{class}} Nclass1,多标签下则全是 0.5),以此约束 z 中不含 label 信息;
同时对 decoder 用重构损失,约束 z’ = (s, z) 能编码原始数据的全部信息,而没有信息丢失。
Practice
Model
小改了一下模型,加了一个分类器 C l f x Clf_x Clfx,对 x 和 x ^ \hat x x^ 进行分类:
Objectives
整幅计算图分三个子模块迭代训练:
-
E
n
c
s
,
C
l
f
s
,
C
l
f
x
Enc_s, Clf_s, Clf_x
Encs,Clfs,Clfx
对 l s = C l f s ( E n c s ( x ) ) l_s=Clf_s(Enc_s(x)) ls=Clfs(Encs(x)) 和 l x s u p = C l f x ( x ) l_x^{sup}=Clf_x(x) lxsup=Clfx(x) 用分类损失; -
C
l
f
z
Clf_z
Clfz
定住 E n c z Enc_z Encz,对 l z = C l f z ( E n c z ( x ) ) l_z=Clf_z(Enc_z(x)) lz=Clfz(Encz(x)) 用分类损失; -
E
n
c
z
,
D
e
c
Enc_z, Dec
Encz,Dec
定住 E n c s Enc_s Encs,对 x ^ = D e c ( E n c s ( x ) , E n c z ( x ) ) \hat x=Dec(Enc_s(x), Enc_z(x)) x^=Dec(Encs(x),Encz(x)) 用重构损失;
另外抽样图像和标签 x ′ , l ′ x', l' x′,l′,对 l x u n s = C l f x ( D e c ( E n c s ( x ′ ) , E n c z ( x ) ) ) l_x^{uns}=Clf_x(Dec(Enc_s(x'), Enc_z(x))) lxuns=Clfx(Dec(Encs(x′),Encz(x))) 用分类损失,target label 是新抽样的 l ′ l' l′;
定住 C l f z Clf_z Clfz,对 l z = C l f z ( E n c z ( x ) ) l_z=Clf_z(Enc_z(x)) lz=Clfz(Encz(x)) 用分类损失,但此时 target label 是 l ~ = ( 1 N c l a s s , … , 1 N c l a s s ) \tilde l=(\frac{1}{N_{class}},\dots,\frac{1}{N_{class}}) l~=(Nclass1,…,Nclass1);
详见代码。
Code
- 用预设参数运行
from time import time
import argparse
import numpy as np
from sklearn import manifold
import matplotlib.pyplot as plt
import keras
import keras.backend as K
from keras.optimizers import adam, sgd
from keras.datasets import mnist
from keras.utils import to_categorical
from keras.models import Model
from keras.layers import Dense, Dropout, Activation, Input, Concatenate, LeakyReLU
np.random.seed(int(time()))
parser = argparse.ArgumentParser()
parser.add_argument('--EPOCH', type=int, default=30)
parser.add_argument('--BATCH', type=int, default=128)
parser.add_argument('--DIM_Z', type=int, default=16)
parser.add_argument('--DIM_H', type=int, default=256)
parser.add_argument('--DIM_FEA', type=int, default=16)
opt = parser.parse_args()
print(opt)
(I_train, L_train), (I_test, L_test) = mnist.load_data()
N_PIX = I_train.shape[1]
I_train = I_train.reshape(I_train.shape[0], -1) / 255.
I_test = I_test.reshape(I_test.shape[0], -1) / 255.
L_train = to_categorical(L_train, 10)
L_test = to_categorical(L_test, 10)
print(I_train.shape, L_test.shape)
N_CLASS = L_train.shape[-1]
DIM_IMG = I_train.shape[-1]
DIM_FEA = opt.DIM_FEA
DIM_Z = opt.DIM_Z
DIM_H = opt.DIM_H
EPOCH = opt.EPOCH
BATCH = opt.BATCH
def Encoder(dim_in=DIM_IMG, dim_z=DIM_Z, name='encoder'):
inputs = Input([dim_in])
x = inputs
x = Dense(DIM_H, activation='relu')(x)
x = Dropout(0.2)(x)
x = Dense(DIM_H, activation='relu')(x)
x = Dropout(0.2)(x)
z = Dense(dim_z)(x)
return Model(inputs, z, name=name)
def Decoder(dim_z=DIM_Z, dim_a=DIM_FEA, dim_out=DIM_IMG, name='decoder'):
z = Input([dim_z])
a = Input([dim_a])
inputs = [z, a]
x = Concatenate()([z, a])
for _ in range(2):
x = Dense(DIM_H, activation='relu')(x)
# x = LeakyReLU(alpha=0.2)(x)
x = Dropout(0.3)(x)
x = Dense(dim_out)(x)
x = Activation("sigmoid")(x)
output = x
return Model(inputs, output, name=name)
def Classifier(dim_in=DIM_Z, n_class=N_CLASS, name='classifier'):
inputs = Input([dim_in])
x = inputs
# x = Dense(DIM_H, activation='relu')(x)
# x = Dropout(0.2)(x)
x = Dense(n_class, activation='softmax')(x)
output = x
return Model(inputs, output, name=name)
def _set_train(m, is_train=True):
m.trainable = is_train
for ly in m.layers:
ly.trainable = is_train
# network
in_lab = Input([N_CLASS])
in_img = Input([DIM_IMG])
other_i = Input([DIM_IMG])
enc_z = Encoder(DIM_IMG, DIM_Z, 'enc_z')
enc_s = Encoder(DIM_IMG, DIM_FEA, 'enc_s')
dec = Decoder(DIM_Z, DIM_FEA, DIM_IMG, 'dec')
clf_z = Classifier(DIM_Z, N_CLASS, 'clf_z')
clf_s = Classifier(DIM_FEA, N_CLASS, 'clf_s')
clf_x = Classifier(DIM_IMG, N_CLASS, 'clf_x')
z = enc_z(in_img)
s = enc_s(in_img)
x_hat = dec([z, s])
l_z = clf_z(z)
l_s = clf_s(s)
l_x_sup = clf_x(in_img)
other_s = enc_s(other_i)
other_x_hat = dec([z, other_s])
l_x_uns = clf_x(other_x_hat)
# enc_s & clf_s & clf_x
m_sup = Model([in_img, in_lab], [l_s, l_x_sup],
name='train_EncF_ClfF_ClfI')
m_sup.compile('adam',
loss=['categorical_crossentropy',
'categorical_crossentropy'],
loss_weights=[1, 1],
metrics=['categorical_accuracy'])
# adv: clf_z
m_adv = Model(in_img, l_z, name='train_EncZ')
_set_train(enc_z, False)
m_adv.compile(sgd(0.001),
loss='categorical_crossentropy',
metrics=['categorical_accuracy'])
# AE: enc_z & dec
m_ae = Model([in_img, other_i], [x_hat, l_z, l_x_uns], name='train_ae')
_set_train(enc_z, True)
_set_train(dec, True)
_set_train(enc_s, False)
_set_train(clf_z, False)
_set_train(clf_x, False)
# _set_train(clf_s, False)
# _set_train(model_lab, False)
m_ae.compile('adam',
loss=['binary_crossentropy', 'categorical_crossentropy',
'categorical_crossentropy'],
loss_weights=[10, 10, 1],
metrics=['categorical_accuracy'])
def TSNE(X, label, title="", save_f=None):
n_points = len(X)
n_components = 2
color = np.argmax(label, axis=-1)
fig = plt.figure(figsize=(15, 8))
if title == "":
plt.suptitle("%s Manifold Learning with %i points"
% (title, n_points), fontsize=14)
else:
plt.suptitle(title)
if X[0].size == 3:
ax = fig.add_subplot(251, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color,
cmap=plt.get_cmap("rainbow"))
ax.view_init(4, -72)
t0 = time()
tsne = manifold.TSNE(n_components=n_components, init='pca', random_state=0)
Y = tsne.fit_transform(X)
t1 = time()
print("t-SNE: %.2g sec" % (t1 - t0))
plt.scatter(Y[:, 0], Y[:, 1], c=color, cmap=plt.get_cmap("rainbow"))
plt.colorbar()
plt.title("t-SNE (%.2g sec)" % (t1 - t0))
plt.axis('tight')
if save_f is not None:
assert isinstance(save_f, str)
fig.savefig(f'./picture/{save_f}.png')
plt.show()
def test():
idx = np.random.choice(L_test.shape[0], 10)
other_idx = np.random.choice(L_test.shape[0], 10)
print('original')
x = I_test[idx].reshape(-1, N_PIX, N_PIX)
x = np.hstack(x)
plt.imshow(x, cmap='Greys')
plt.show()
print('reconstruct')
x_gen = dec.predict([enc_z.predict(I_test[idx]),
enc_s.predict(I_test[idx])])
x = x_gen.reshape(-1, N_PIX, N_PIX)
x = np.hstack(x)
plt.imshow(x, cmap='Greys')
plt.show()
print('change s:', np.argmax(L_test[other_idx], axis=-1))
x_gen = dec.predict([enc_z.predict(I_test[idx]),
enc_s.predict(I_test[other_idx])]) # changed
x = x_gen.reshape(-1, N_PIX, N_PIX)
x = np.hstack(x)
plt.imshow(x, cmap='Greys')
plt.show()
print('change z:', np.argmax(L_test[idx], axis=-1))
x_gen = dec.predict([enc_z.predict(I_test[other_idx]), # changed
enc_s.predict(I_test[idx])])
x = x_gen.reshape(-1, N_PIX, N_PIX)
x = np.hstack(x)
plt.imshow(x, cmap='Greys')
plt.show()
print('real label:', np.argmax(L_test[idx[0]], axis=-1))
print('clf_z:', clf_z.predict(enc_z.predict(I_test[idx[0:1]]))[0])
print('clf_s:', clf_s.predict(enc_s.predict(I_test[idx[0:1]]))[0])
def gen_data(dataset, batch_size):
"""数据生成器"""
if dataset == "train":
I, L = I_train, L_train
elif dataset == "test":
I, L = I_test, L_test
size = I.shape[0]
while True:
idx = np.random.choice(size, batch_size)
yield I[idx], L[idx]
xjb_label = np.ones((BATCH, N_CLASS)) / N_CLASS # 假 label
gen_train = gen_data('train', BATCH)
for epoch in range(EPOCH):
print(f'--- {epoch} ---')
for b in range(I_train.shape[0] // BATCH):
for _ in range(1):
i, l = next(gen_train)
loss_sup = m_sup.train_on_batch([i, l], [l, l])
for _ in range(3):
i, l = next(gen_train)
loss_adv = m_adv.train_on_batch(i, l)
for _ in range(1):
i, l = next(gen_train)
i2, l2 = next(gen_train)
loss_ae = m_ae.train_on_batch([i, i2], [i, xjb_label, l2])
print(loss_sup)
print(loss_adv)
print(loss_ae)
if epoch % 10 == 0:
test()
print('\n--- after ---')
test()
TSNE(enc_z.predict(I_test), L_test, 'z distribution')
TSNE(enc_s.predict(I_test), L_test, 's distribution')
Renderings
原图、重构图、换 s 不换 z、换 z 不换 s

s 的分布
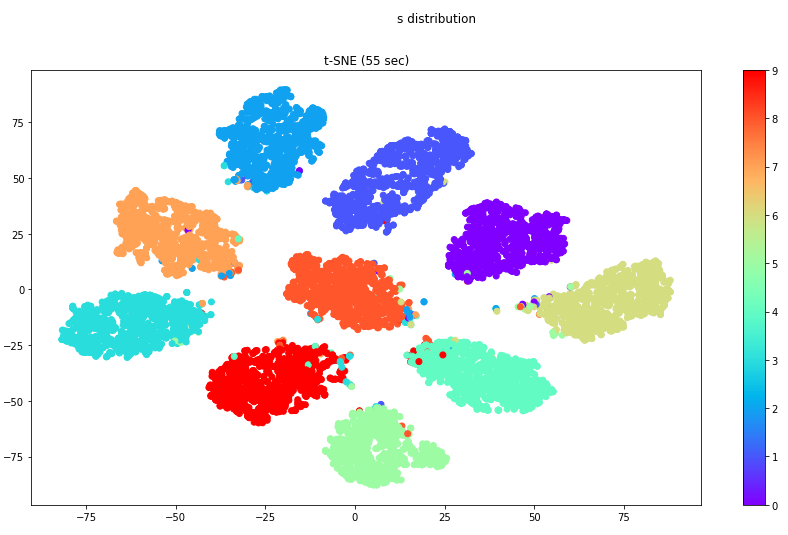
z 的分布
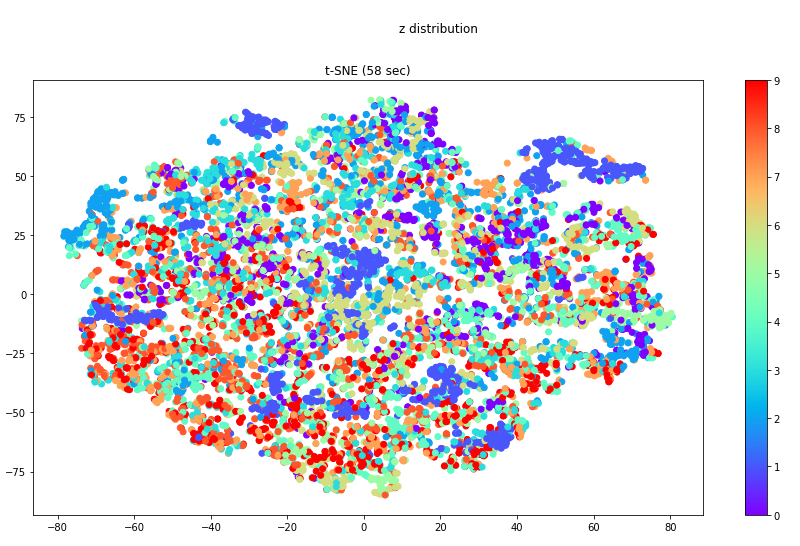





















 1953
1953

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








